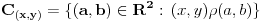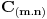[ mico91 @ 12.04.2013. 12:31 ] @
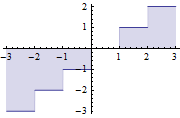
| Pozdrav svima. Imam problema sa sledećim zadatkom: Data je relacija ekvivalencije u skupu R^2 takva da je (x,y)ρ(a,b) <=> [x] = [a] i [y] = [ b ] . Odrediti klase ekvivalencije. Dati geometrijsku interpretaciju. Naime, nisam baš siguran kako bih odredio klasu ekvivalencije ovog skupa, jer sve što sam do sada radio jeste bilo u skupu R, a ne mogu naći nigdje sličan primjer sa postupkom riješavanja u skupu R^2. |