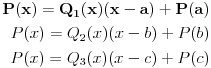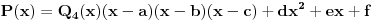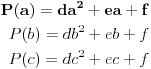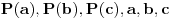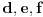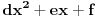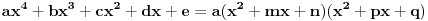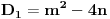[ Neprekidan @ 14.04.2013. 21:17 ] @
| Kako ispitati da li realan polinom četvrtog stepena ima realnih nula, BEZ faktorizacije? Ako znamo ostatak pri dijeljenju realnog polinoma sa polinomima x-a i x-b i x-c, kako odrediti ostatak pri dijeljenju tog polinoma sa (x-a)(x-b)(x-c)? |