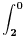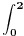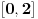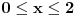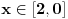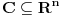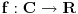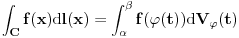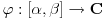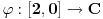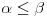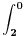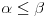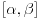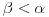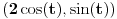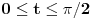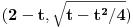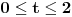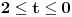[ miki069 @ 18.04.2013. 21:39 ] @
| Da ne prekucavam, u pitanju je treći zadatak sa prvog kolokvijuma: http://imi.pmf.kg.ac.rs/moodle...vni_kolokvijumi-25.06.2011.pdf Ako elipsu prevedem u parametaski oblik: X=2*cos(t), Y=sin(t), gde usmereno od tačke A do B, t uzima vrednosti od nula do PI/2, izračunam ds, na kraju dobijem vrednost integrala 14/9. Ako elipsu prevedem u esplicitno rešen Y u f-ji od X, gde X uzma vrednosti od 2 do nula, izračunam ds, na kraju dobijem vrednost integrala -14/9. Rezultat treba da bude isti. Mislim da je tačno rešenje 14/9. Zbunjuje me kako iz eksplicitnog oblika dobijam -14/9? Iz eksplicitnog oblika funkcija nije diferencijabilna za X=2, ali u proizvodu Y*ds se skrati sporni koren. Probavao sam i verziju sa sklaćenim lukom (da ne ide od tačke A) da bi Y bio diferencijabilan u svim tačkama linije. Opet iz parametaskog oblika dobijem pozitivnu vrednost integrala, a iz eksplicitnog istu vrednost ali negativnu. Rađeno više puta. Ako je potrebno okačiću i celo rešenje. [Ovu poruku je menjao miki069 dana 19.04.2013. u 22:05 GMT+1] |