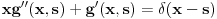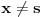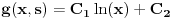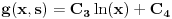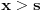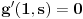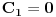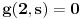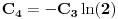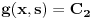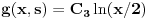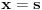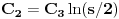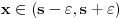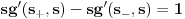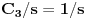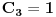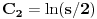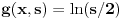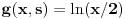[ ilija90 @ 03.05.2013. 08:46 ] @
| Pozdrav, Imam pitanje za jedan zadatak: "Odrediti Greenovu funkciju konturnog problema xy''+y'=f(x), y'(1)=0, y(2)=0 a potom odrediti partikularno resenje date diferencijalne jednacine." Jel moze neko da mi objasni kako se ovo radi? Nalazio sam na googlu neke stvari o Grinovoj funkciji na engleskom jeziku ali sve je bila teorija i nisam uspeo da skontam kako se radi. Znam da prvo treba da se nadje resenje homogene diferencijalne jednacine, xy''+y'=0. Opste resenje ove jednacine je y(x)=C1*ln(x)+C2. |