Probaj da proizvod za i=1 i i=16 pretvoriš u zbir.
Isto tako za i=2 i i=15.
Pa za i=3 i i=14.
...i=8 i i=9.

Ili neke da pretvaraš u zbir, a neke da ne diraš.

Rešenje je prosto. Treba da svodiš sve na uglove u opsegu . Ako je , onda je . Onda ideš sa dupliranjem uglova pa dobijaš da je

,
,

,

pa je

.

Ovo je isto što i

.

Drugim rečima je

.

Zatim kreneš od , pa opet udvostručavaš uglove dobijajući

,

odnosno

.

Konačno je

,

odnosno obzirom da je ,

.

A evo i malo opstijeg rezultata, ako ja nisam negde pogresio, a to je , gde predstavlja imaginarnu jedinicu.

U nasem konkretnom slucaju imali bismo

A evo i postupka kako mozemo doci do ove formule:

.

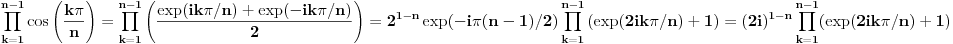
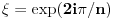
Naravno, sada je kljuc naci . Verovatno sam deo koji predstoji zakomplikovao nepotrebno. Prvo, uvedimo oznaku (hint = ciklotomicni polinom) . Sada je .

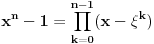
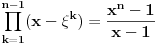
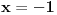
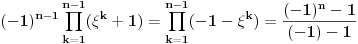
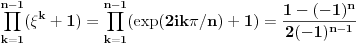
Poznata nam je obrazac , a sa druge strane vazi . Dakle, vazi . Stavljajuci nalazimo , odnosno . A odatle lako nalazimo da vazi .

S tim da se taj izraz može uprostiti, što znači da "nisi prepisivao" ;).



Konačno je

.

Odnosno, za parno to je , a za neparno to je .

Odlično Sonec!

Pretpostavljam da je moguce na isti nacin uraditi i proizvod sa sinusima? Da se tamo kod onog ciklotrona :) stavi x=1...
I da li se onda moze uspostaviti veza sa proizvodom , koji se lako racuna?

,
,
,
,
.

Hvala na odgovorima ali ja ništa od ovoga ne razumem :(
Mnogo bi mi značilo da neko detaljnije razjasni prvi Nedeljkov odgovor. Kao prvo, kako to misliš svesti na (0, Pi) ? Zar nisu svi uglovi već u tom opsegu?
Drugo, šta podrazumevaš pod "udvostručavanjem uglova" ? Kosinus dvostrukog ugla?

Evo ovako: Koristiš formulu za sinus dvostrukog ugla:

.

E, sad, pođi od .



Sad isto to uradi polazeći od .

.

E to je to. Hvala.

Moj pokušaj je bio nešto nalik ovome ali me je zbunilo to što se preskaču neki činioci udvostručavanjem. Nije mi pala na pamet ideja da iz više prolaza "pohvatam" sve.

Hvala puno.

Darko: Taj proizvod se "lako" racuna preko geometrijskog reda. A sad, da li formule za proizvod sinusa i kosinusa mogu posluziti da se taj proizvod izracuna pomocu njih? Ne znam. Ne izgleda ocigledno.

Pogledaj račun malo iznad.

Nedeljko, pogledaj sta je Darko pitao. Nisam mislio na te proizvode.

Sonec, ono sto sam ja mislio je da je , ako nisam nesto pogresio...

Sa druge strane je , pa se mozda mogu iskoristiti formule koje ste ovde izveli ti i Nedeljko... Ne izgleda ocigledno, svakako, ali eto to mi je palo na pamet...

Ja mislim da sam tako nesto i rekao u mojoj poruci :)
Razumeli smo se.