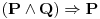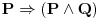pa, uglavnom ako razumes pitanje nekog zadatka, skoro pa si ga resio.
ovo kako si postavio- ja nisam siguran da znam sta se zapravo tu trazi...sta je uslov, sta iskaz, da li su povezani, a to je potrebno znati da bi odgovorio sta je cemu potrebno i dovoljno.

uglavnom se "problem" zadatka u matematici sastoji u tome sto sastavljac pravi terminoslosku i/ili pojmovnu zbrku koja skriva sustinu pitanja, a koja je uglavnom prosta.

i kada otkrijes tu sustinu onda u ogromnom ili najvecem broju slucajeva zadatak resavas lagano, ako ti je poznata materija, naravno. mali broj zadataka koje je tesko resiti se vecinom odnose na oblasti koje nauka jos dovoljno nije razjasnila, ili cak uopste.

tako da, nemoj da se zbunjujes, nema teskih pitanja ;)

mislim da nije lose ako preformulises prvu recenicu zadatka, u oblik koji ce ti biti razumljiv. eto kao predlog.

Ja bih stavio pod d);
Nije mu potreban a nije mu ni dovoljan zato sto je proizvoljni iskaz. A proizvoljni iskaz se moze dopunjavati do u beskonacnost te je zato DOVOLJAN nekako "out"!?

evo da preformulisamo:
-imamo 2 proste recenice "p" i "q", koje nisu povezane.

zadatak ustvari krije dva pitanja:
-da li je "p i q" uslov za "p"
-ako jeste- da li je potreban i/ili dovoljan.

u konkretnom primeru, to bi moglo da bude:

p: jedem sendvic
q: u indoneziji pada kisa

dakle, ako je "jedam sendvic i u indoneziji pada kisa", prvo pitanje je:

-da li je to uslov za "jedam sendvic"?

iskreno nemam pojma :D, ovo mi bas i nema previse smisla.

valjda neko bude znao ;)

Može nastupiti jedan od 4 slučaja:
Ni P ni Q
P da Q ne
P ne Q da
I P i Q
U drugom i četvrtom slučaju imamo P.Bilo koji od njih je dovoljan uslov. Nužno je da nastupi bar jedan od ta dva,ali nije potrebno da to bude baš drugi ili baš četvrti slučaj.

Dakle P^Q nije potreban,ali jeste dovoljan uslov da se desi P.Odgovor 1.

Dovoljan je jer je u opštem slučaju 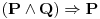tačno, tj. to je tautologija.

U opštem slučaju nije potreban jer 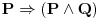nije tautologija.

Drugim rečima, ako je tačno i P i Q, onda svakako mora P biti tačno, ali ako je P tačno, i dalje ne moraju biti tačna oba iskaza P i Q.

htp, mislim da je jasnije, barem meni, ako preformulises postavku ovako:

neka su p i q nezavisni izrazi. ako je "p i q" tacno, da li iz toga mozemo da odgovorimo- da li je i p tacno?

ako da, to je onda dovoljno informacija, tj dovoljan uslov.

U zadatku piše da su P i Q proizvoljni iskazi. Niko ne kaže da su nezavisni, niti mi je poznat taj pojam iz logike. Svi iskazi se dele u dve klase - tačnih i netačnih iskaza i svi iskazi iz iste klase su ravnopravni.

Ovde bi "proizvoljan" trebalo tumačiti kao "nepoznat". Zadatak bi zapravo trebao da glasi: Ako su P i Q iskazi, iskaz P&Q je za iskaz P u opštem slučaju samo dovoljan.

Kako bilo...Hvala na paznji! Ja ostajem za pod d).

Onda nisi naučio pojam dovoljnog uslova. Pročitaj definiciju.

@htp,
ako ce ti biti lakse, ni meni nista sad nije jasno :)). malo sam razmislio, i sad mislim da je odgovor c), i potreban i dovoljan.

mislim da ti treba konkretan primer da ovo usvojis, jer ovako prikazano je cista apstrakcija i mislim da ne bi trebalo napamet da kontas.

evo ti skoro isti zadatak na ovom forumu, i objasnjenja kroz konkretne primere.

http://arhiva.elitesecurity.org/t452273-Logika-zadatak

mozda ti bude od pomoci za ovo sada.

Apstraktna petljavina sa uslovima "dovoljan" i "potreban" je dobar primjer zbog čega se matematika nekim đacima zgadi.
Šta neko pomisli ako pokušava naučiti osnovne pojmove pa pročita:
"Nešto je dovoljno ako je to tautologija,ali nije potrebno ako to nije tautologija."
Prasne u blesav smijeh od muke,batali sve i ode na pivo.

Apstrahiranje počiva na seriji konkretnih primjera.

Moze i preko piva - recimo da mi treba jedno pivo:

ako imam dva, znaci da imam i jedno, dakle dva piva su mi dovoljna :)

ali dva piva mi nisu potrebna (neophodna), jer mi treba samo jedno...

jeste, jeste...@Nedeljko u pravu si...ja sam se zanio previse proizvoljnim iskazima...

Darko je dao baš dobar primer.
Samo neka P bude "treba mi Jelen pivo", a Q "treba mi Lav pivo".
Čisto da P i Q budu različiti iskazi.

@miki069
Bas tako. Mislio sam se sta bi mogao da uzmem umesto piva, nisam se setio da uzmem dve vrste :) I na kraju ostavio tako, jer je logika zadovoljena (nisam koristio to sto je P=Q). U svakom slucaju, sada je primer upotpunjen...