[ panterloki @ 22.05.2013. 07:53 ] @
|
| Kako, i da li se moze odrediti treca stranica trougla na osnovu zadate dve stranice i poluprecnika upisanog ili opisanog kruga trougla? |
[ darkosos @ 22.05.2013. 08:31 ] @
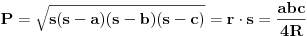
.
[ panterloki @ 22.05.2013. 08:53 ] @
Nemam zadatu povrsinu samo stranice a i b i poluprecnik upisnaog ili opisanog kruga.
[ darkosos @ 22.05.2013. 09:26 ] @
Da, znam, koristi one jednakosti i ne gledaj na P. To sam napisao samo da bih naglasio da su to sve formule za povrsinu.
[ panterloki @ 22.05.2013. 09:33 ] @
Znaci iz toga imam sledce:
s^4-s^3*c-s^3*b-s^2*b*c-s^3*a+s^*a*c+s^2*b*c+a*b*c*s-r^2*s^2=0
gde je s=(a+b+c)/2
Kako sad odavde da izrazim neku od stranica?
[ darkosos @ 22.05.2013. 09:47 ] @
Ne znam, nisam probao... Mozes prvo da skratis sa s, pa da posle uvrstis formulu za s... Dobice se izgleda jednacina treceg stepena, koja jeste resiva. U svakom slucaju, ovo ti je algebarski pristup. Ako hoces, mozes da probas da nacrtas pa koristis veze koje se "vide". Recimo za opisani krug, konstrukcija izgleda prosto: nacrtas krug, pa iz jedne tacke dve tetive u duzini datih stranica, i treca je iznudjena. Mozda bi tada mogao da izracunas ugao izmedju datih stranica, pa to iskoristis za racun trece... Ne mogu sad da resavam zadatak, ali eto to su neke ideje...
[ lonelyrider_44 @ 22.05.2013. 10:25 ] @
Ako je dato
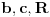
, ugao

možeš naći pomoću sinusne teoreme, a stranicu

pomoću kosinusne.
[ djura63 @ 25.05.2013. 10:15 ] @
ima li neko resenje za ovaj zadatak:
[ Sonec @ 25.05.2013. 10:59 ] @
Pa, kako je ovo jednokostranicni trougao (
) to mozes odrediti poluprecnik upisanog kruga (1/3 visine), a taj poluprecnik upisanog je poluprecnik opisanog kruga (oko trougla sa stranicom

) koji zavisi od

. Odatle nadjes

, a posle lako i povrsinu osencenog dela. Ovaj podatak od
je nepotreban, prema mom misljenju.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.