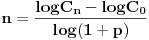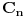[ soni @ 22.05.2013. 08:33 ] @
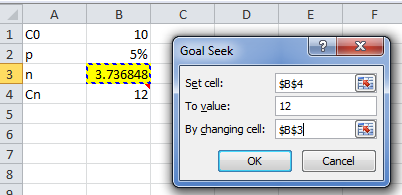
| cesto u svom poslu moram raditi sa proracunima svih tipova vezanih uz stope rasta, izracun prosjecnih stopa i sl. U tu svrhu mi pomaze pomocna tablica u excelu. E sad ako znamo da je konacna vrijednost Cn=Cox(1+p)^n, gdje je Co-pocetna vrijednost, p- prosjecna stopa rasta, a n - vrijeme u godinama, kako i te formule dobiti n - tj broj godina. Dakle kako na osnovu te osnovne formule, kad imamo pocetnu vrijednost, konacnu vrijednost i prosjecnu stopu rasta, dobiti za koliko godina pocetna vrijednost dospije na konacnu vrijednost uz odredjenu godisnju stopu rasta?? Hvala lijepo na svakoj pomoci! |