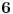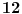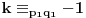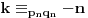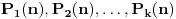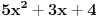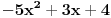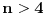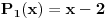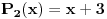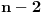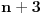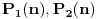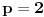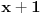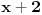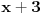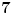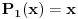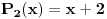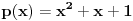|
|
[ number42 @ 28.05.2013. 22:52 ] @
|
| zanima me za jednu hipotezu o prostim brojevima da li vec postoji.
palo mi na pamet, pa tako, zanima me.
pregledao sam otprilike sve varijante goldbahove hipoteze verujuci da cu mozda naici na nju, ali ne postoji ili je ja nisam nasao.
a glasila bi ovako recimo:
"za svaki prost broj (Pb1) postoji beskonacno mnogo prostih brojeva (Pbx) koji kada se pojedinacno saberu sa Pb1 i brojem 1 daju neki prost broj (Pb2)".
moguce da je drugacije formulisana, ali nema sanse da je nadjem. a nemam pojma ni da li je tacna.
to bi bilo, po formuli Pb1+Pbx+1=Pb2, npr:
Pb1=3
3+19+1=23
3+43+1=47
3+67+1=71
itd...
ili
Pb1=29
29+31+1=61
29+37+1=67
29+41+1=71
itd...
dakle, da li ovo vec postoji drugacije formulisano?
|
[ Igor Gajic @ 29.05.2013. 00:04 ] @
http://en.wikipedia.org/wiki/Goldbach's_conjecture
Dosta sire, ali tvoja hipoteza trivijalno sledi i ostavlja se citaocu za domaci.
[ Bojan Basic @ 29.05.2013. 00:22 ] @
Drugim rečima, tvoja hipoteza pretpostavlja da postoji beskonačno mnogo parova prostih brojeva koji se razlikuju za  , kao i beskonačno mnogo parova prostih brojeva koji se razlikuju za 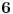 , pa isto to za razliku  , pa isto to za 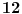 ... (brojevi koje sam navodio predstavljaju neparne proste brojeve uvećane za  ). Za svaki ovaj slučaj postoji hipoteza da takvih parova prostih brojeva ima beskonačno mnogo, i to ne samo za ove tvoje slučajeve nego za bilo koji paran broj na mestu razlike. Verovatno najpoznatiji slučaj jeste za razliku jednaku  , i takvi parovi prostih brojeva zovu se prosti blizanci. Dalje, za razliku  imamo rođačke proste brojeve, za razliku 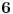 seksi proste brojeve seksi proste brojeve itd. Hipoteza koja sve ovo objedinjuje (a zapravo pretpostavlja i mnogo više od toga) jeste recimo Diksonova hipoteza, a njeno dalje uopštenje je Šincelova H-hipoteza.
Citat: Igor Gajic:
Dosta sire, ali tvoja hipoteza trivijalno sledi i ostavlja se citaocu za domaci.
Kako misliš da ovo sledi iz Goldbahove hipoteze? [ number42 @ 29.05.2013. 01:08 ] @
@bojan basic,
da, to je to.
ovaj slucaj sa bilo kojim parnim brojem kao razlikom mi se cini neodredjeniji, jer bas sam hteo da idem na tri prosta, a time se svodi na dva.
imam neku ideju da bi mozda gomilanjem raznih nezavisnih hipoteza o prajmovima mogao da se nadje sablon, ma koliko bio komplikovan, jednostavno njihovim ukrstanjem.
ne znam koliko sam ovo dobro objasnio a ni da li sam u pravu, al eto... 
zahvaljujem, bas cu pregledati i sincelovu i diksonovu hipotezu, prvi put cujem za njih.
@igor gajic,
nisam uspeo da vidim kako ovo sledi iz goldbahove hipoteze a bas sam hteo da se ne bih ponavljao, ako mozes da objasnis sta si mislio. [ Igor Gajic @ 29.05.2013. 01:47 ] @
Moja greska, preskocio sam "beskonacno mnogo" deo.
[ plague @ 29.05.2013. 10:15 ] @
Citat: Bojan Basic:
Za svaki ovaj slučaj postoji hipoteza da takvih parova prostih brojeva ima beskonačno mnogo, i to ne samo za ove tvoje slučajeve nego za bilo koji paran broj na mestu razlike.
Mislim da je podvucen deo skoro opovrgnut link
Citat: On April 17, 2013, Zhang announced a proof that there are infinitely many pairs of prime numbers with a gap at most 70 million.
Osim ako nisam pogresno shvatio jer nisam matematicar, u tom slucaju bih voleo da mi neko objasni sta je zapravo dokazao ako nije to. [ Nedeljko @ 29.05.2013. 10:34 ] @
Nisi razumeo tu teoremu koju linkujes.
Ne tvrdi se da za paran broj veci od 70 miliona nema beskonacno mnogo parova brojeva koji se razlikuju za toliko (negativan rezultat), vec da ima beskonacno mnogo parova koji se ne razlikuju za vise od 70 miliona (pozitivan rezultat).
[ plague @ 29.05.2013. 10:52 ] @
Samo da potvrdim:
I dalje postoje prosti parovi cija je razlika beskonacno veliki paran broj, ali razlika izmedju 2 susedna prosta broja nikada ne moze biti veca od 70m?
Edit: Shvatam gde je bila greska, par ne moraju biti dva susedna prosta broja u onome sto je Bojan rekao.
[ Nedeljko @ 29.05.2013. 11:28 ] @
Postoje proizvoljno dugi nizovi uzastopnih slozenih brojeva, pa cak i brojeva koji nisu stepeni prostih. Imali smo ovde na forumu dokaz. To je bio zadatak sa jedne od matematickih olimpijada.
Broj nije stepen prostog broja akko je deljiv sa bar dva prosta broja, tj. proizvodom nekih razlicitih prostih brojeva. Izaberimo bilo koji prost broj  i  prostih brojeva  , sto je moguce uciniti jer po Euklidovoj teoremi prostih brojeva ima beskonacno mnogo. Da bi vazilo

potrebno je i dovoljno da vazi
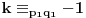 ,
...
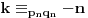 .
Obzirom da su brojevi  uzajamno prosti, po Kineskoj teoremi o ostacima postoji beskonacno mnogo resenja gornjeg sistema kongruencija u skupu prirodnih brojeva (tacno jedno do na kongruencju po modulu  ), pa nijedan od brojeva  nije cak ni stepen prostog broja.
Teorema koju si citirao tvrdi da postoji beskonacno mnogo parova uzastopnih prostih brojeva cija razlika nije veca od 70 miliona, odnosno da postoji bar jedan paran broj m koji nije veci od 70 miliona tako da ima beskonacno mnogo parova uzastopnih prostih brojeva koji se razlikuju za m. [ Bojan Basic @ 29.05.2013. 14:34 ] @
Citat: Bojan Basic:
Za svaki ovaj slučaj postoji hipoteza da takvih parova prostih brojeva ima beskonačno mnogo, i to ne samo za ove tvoje slučajeve nego za bilo koji paran broj na mestu razlike.
Zanesoh se pričajući o uopštenjima u vidu Diksonove i Šincelove hipoteze, pa sam propustio da pomenem kako se baš ova hipoteza zove: to je Polinjakova hipoteza. [ darkosos @ 29.05.2013. 15:05 ] @
Cini mi se da postojanje rupa ("gaps") nije isto sto i mogucnost predstavljanja prostog broja kao zbira neka dva prosta. Rupa koja se popunjava parnim brojem (nastalim kao prost + 1), ne mora biti prava rupa, tj. da izmedju nema prostih brojeva, pa bih rekao da je Polinjakova hipoteza jaca od ove o kojoj se ovde prica... Dakle ako vazi Polinjakova, vazice i postavljena, ali ne i obrnuto.
[ number42 @ 29.05.2013. 15:23 ] @
@igor gajic,
ma ok je, nema veze.
@plague,
hvala za link. nisam bas siguran da je ono dobro objasnjeno, a jos je na engleskom...
koliko razumem, dokaz je od fundamentalne vaznosti za proste brojeve, a govori da kada idemo u beskonacnost, razmaci izmedju najblizih prostih brojeva se nece uvecavati (a to bi valjda bilo logicno), nego se uvek vrte tu negde u istom intervalu [2,70mil] bez obzira o koliko velikoj cifri se radi.
@bojan basic,
pregledao sam obe hipoteze, ali nazalost nisu prevedene, ima samo ne engleskom na celom netu, a povrsno znanje engleskog nije dovoljno za razumevanje.
dok sam ovu prvu koliko toliko pohvatao, ovu drugu nisam skapirao, plus sto baca reference na jos neke druge stvari, tako da sam mislio ako imas vremena da ukratko objasnis ovu h-hipotezu, onako najprostije.
naravno, ako te mrzi nije frka.
@plague,
zaboravio sam. ako nadjes negde postupak dokazivanja, molim te da linkujes, bas me zanima.
[ number42 @ 29.05.2013. 15:28 ] @
Citat: darkosos:
ako vazi Polinjakova, vazice i postavljena, ali ne i obrnuto.
mislim da ne, tj medjusobno se ne iskljucuju.
EDIT: ustvari cek naci cu primer pa cu dopuniti.
znaci ovako: polinjakova hipoteza se moze preformulisati na sledeci nacin:
"za svaki prost broj (Pb1) postoji beskonacno mnogo nekih neparnih brojeva (2n+1) od kojih svaki pojedinacno kada se sabere sa Pb1 i brojem 1 daje neki prost broj (Pb2)".
a hipoteza iz prvog posta glasi:
"za svaki prost broj (Pb1) postoji beskonacno mnogo nekih prostih brojeva (Pbx) od kojih svaki pojedinacno kada se sabere sa Pb1 i brojem 1 daje neki prost broj (Pb2)".
ako skupove (neki Pbx) i (neki 2n+1) predstavimo kao ono kao krugove, S1 i S2, oni mogu zauzeti sledece polozaje: da se S1 i S2 seku, ili da S1 pripada S2 i vice versa, ili da nemaju zajednickih tacaka.
nekako mi je najblize objasnjene da se S1 i S2 seku, mada nisam siguran da mozemo tvrditi da su i druga dva ishoda nemoguca.
ovo onako na brzinu razmisljanje.
[Ovu poruku je menjao number42 dana 29.05.2013. u 16:54 GMT+1][ plague @ 29.05.2013. 15:33 ] @
@number42 Uploadovacu ga uskoro, mada dokaz nije nimalo jednostavan. Nisam jos uvek procitao, mada i posle citanja skoro sigurno necu razumeti iako me zanima podosta.
Edit: Nisam siguran da li je ovo potencijalni copyright problem, ako moderator smatra da jeste neka ukloni attachment.
[ number42 @ 29.05.2013. 15:58 ] @
Citat: Nisam siguran da li je ovo potencijalni copyright problem
pa sta znam... ja ga skinuo. nema veze, idemo na robiju 
hvala. [ Nedeljko @ 29.05.2013. 16:02 ] @
Citat: number42: govori da kada idemo u beskonacnost, razmaci izmedju najblizih prostih brojeva se nece uvecavati (a to bi valjda bilo logicno), nego se uvek vrte tu negde u istom intervalu [2,70mil] bez obzira o koliko velikoj cifri se radi.
Ne, povecavace se, a kad-tad ce se ponovo pojavljivati nesto malo (manje od 70 miliona). Procitajte apstrakt
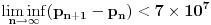 .
Ovo sto vi navodite bi bilo
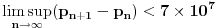 ,
a to nije isto. Stavise, prilozio sam vam jednostavan dokaz da je
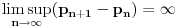 . [ Nedeljko @ 29.05.2013. 16:30 ] @
Ako rupe manje od 70 miliona nazovemo malim i oznacimo sa M, a ostale nazovemo velikim i nazovemo V, njegova teorema tvrdi da nece pocev od nekog mesta biti V,V,V,... vec da u tom nizu mora biti beskonacno mnogo M. Znaci
M,M,M,...,M,V,V,V,...,V,M,V,V,V,...,V,M,V...
Koliko god daleko da idem, javice se neko M, posle koga moze ici ko zna koliko V, pa opet neko M itd, a ne da ce pocev odnekle biti sve M kako vi tumacite.
[ Bojan Basic @ 29.05.2013. 17:12 ] @
Citat: darkosos:
Rupa koja se popunjava parnim brojem (nastalim kao prost + 1), ne mora biti prava rupa, tj. da izmedju nema prostih brojeva, pa bih rekao da je Polinjakova hipoteza jaca od ove o kojoj se ovde prica... Dakle ako vazi Polinjakova, vazice i postavljena, ali ne i obrnuto.
Da, u pravu si. Polinjakova je jača već na osnovu toga što govori o rupama ma koje parne dužine (dok u našem slučaju pričamo samo o onim parnim brojevima koji su za  veći od prostog broja), no ovo što pominješ još je ozbiljnije pojačanje.
Citat: number42:
znaci ovako: polinjakova hipoteza se moze preformulisati na sledeci nacin:
"za svaki prost broj (Pb1) postoji beskonacno mnogo nekih neparnih brojeva (2n+1) od kojih svaki pojedinacno kada se sabere sa Pb1 i brojem 1 daje neki prost broj (Pb2)".
Ne sasvim. Ovo što si ti napisao zapravo je očigledno tačno tvrđenje (fiksiraj broj Pb1, neka je Pb2 bilo koji prost broj veći od Pb1, i tada postoji neparan broj koji kad se sabere sa Pb1 i brojem 1 daje Pb2). Zapravo ono što ti zoveš Pb1 može biti bilo koji neparan broj, a ono gde ti pominješ proizvoljan neparan broj, e tu zapravo treba da stoji prost broj. Samo zameni ta dva pojma i dobićeš preformulaciju Polinjakove hipoteze kakvu si hteo, s tim što, kao što Darko reče, Polinjakova hipoteza još postavlja ograničenje da je Pb2 najmanji prost broj veći od Pbx.
Citat: plague:
Edit: Nisam siguran da li je ovo potencijalni copyright problem, ako moderator smatra da jeste neka ukloni attachment.
Nažalost, ipak jeste. Ostaviću ga još neko vreme da skinu učesnici ove teme koji su zainteresovani, ali moraće da bude uklonjen posle toga.
Citat: number42:
dok sam ovu prvu koliko toliko pohvatao, ovu drugu nisam skapirao, plus sto baca reference na jos neke druge stvari, tako da sam mislio ako imas vremena da ukratko objasnis ovu h-hipotezu, onako najprostije.
Dakle, posmatrajmo polinome 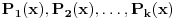 sa celobrojnim koeficijentima, s pozitivnim vodećim koeficijentom i nesvodljive nad prstenom celih brojeva. Neka su ovi polinomi takvi da ni za jedan prost broj  nije ispunjeno da za svaki prirodan broj  broj  deli neku od vrednosti 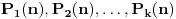 . Tada H-hipoteza tvrdi da postoji beskonačno mnogo prirodnih brojeva  takvih da su sve vrednosti 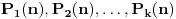 proste. Diksonova hipoteza je specijalan slučaj ove hipoteze, kada su svi posmatrani polinomi linearni.
To bi bilo vrlo ukratko, ali slobodno pitaj ako nešto iz ovog opisa treba bolje razjasniti, rado ću pomoći. [ number42 @ 29.05.2013. 17:35 ] @
@bojan basic,
ok, znaci ono sto sam napisao i nije polinjakova hipoteza. moja greska, mislio sam da znam sta je. sorry svima 
cuj, hvala sto si izdvojio vreme da objasnis h-hipotezu, ali nisam skontao. verovatno mi fali znanja da bih to usvojio na taj nacin.
aj pokusaj da objasnis kao, ne znam, malom detetu ili nekoj babi s romanije  , sigurno cu razumeti.
i malo sam pregledao dokaz ovog japanca, i ono, ok, ovaj je dokazao beskonacnost razmaka izmedju uzastopnih prostih u intervalu [2,70mil], mislim sjajan posao, al sta je radio iznad 70 miliona, da li je dokazao beskonacnost ili konacnost, ili nije dokazao pa je nepoznato... donno. [ Nedeljko @ 29.05.2013. 17:52 ] @
Iznad 70 miliona ili bilo koje druge konačne granice ima beskonačno mnogo pojavljivanja i to je odavno poznato, pa nema potrebe da se razmatra.
Bojane, da li ti primećuješ nerazumevanje materije od strane učesnika? Ako je odgovor pozitivan, pomozi im.
[Ovu poruku je menjao Nedeljko dana 29.05.2013. u 19:03 GMT+1]
[ plague @ 29.05.2013. 18:12 ] @
Moje nedoumice su razjasnjene bas potpuno ovim i narednim postom i zahvaljujem se na tome. :) [ number42 @ 29.05.2013. 18:45 ] @
a da li postoji ova hipoteza, ili ne daj boze dokaz/opovrgavanje:
"izmedju prostog broja (Pb1) i dvostruko veceg broja (2Pb1) se uvek nalazi barem jedan prost broj (Pbs)".
ovo bi zapravo u prevodu znacilo da je udaljenost izmedju dva uzastopna prosta broja uvek limitirana vrednoscu manjeg prostog broja.
zapravo, hocu da vidim da li postoji relacija izmedju velicine gepa i velicine prostog broja.
znaci, ne mogu da zamislim da izmedju 101 i 202 nema prostih brojeva, izmedju 1009 i 2018 nema prostih brojeva, ili milijarduistajaznam i dvemilijardedvaputstajaznam...
[ number42 @ 29.05.2013. 22:43 ] @
Citat: "izmedju prostog broja (Pb1) i dvostruko veceg broja (2Pb1) se uvek nalazi barem jedan prost broj (Pbs)".
hm, tek sada sam video da ovo korespondira sa goldbahovom hipotezom. jer u slucaju da nije tacno, onda bilo koji paran broj ne bi mogao biti zbir dva prosta.
dakle, ako je tacna goldbahova hipoteza, onda bi razmak izmedju dva uzastopna prosta broja uvek bio manji od manjeg prostog broja,
ili
(Pn2-Pn1)<Pn1
a ovo bi moglo i da se uopsti, tako da bi izvedena hipoteza bila:
"izmedju bilo kog broja n i njegove dvostruke vrednosti 2n uvek je smesten barem jedan prost broj".
tako da sa sigurnoscu znamo da izmedju 10 hiljada i 20 hiljada postoji barem jedan prost broj, izmedju 10 milijardi i 20 milijardi je uvek jedan prost broj, i tako u beskonacno...
ne znam da li ove izvedene hipoteze imaju nekog znacaja, al eto...
[ Bojan Basic @ 02.06.2013. 23:11 ] @
Citat: number42:
cuj, hvala sto si izdvojio vreme da objasnis h-hipotezu, ali nisam skontao. verovatno mi fali znanja da bih to usvojio na taj nacin.
aj pokusaj da objasnis kao, ne znam, malom detetu ili nekoj babi s romanije  , sigurno cu razumeti.
Ajde da probam postupnije (kasnim nekoliko dana zato što sam bio u priličnoj gužvi, tek sad sam uspeo da odvojim malo vremena).
Neka je 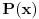 polinom s celobrojnim koeficijentima (to, pretpostavljam, znaš šta je); u celoj poruci govorimo isključivo o polinomima s celim koeficijentima.
E sad, nećemo posmatrati baš bilo kakav polinom, nego tražimo da taj polinom ispunjava određene uslove. Prvo, vodeći koeficijent treba da mu bude pozitivan (znači, polinom 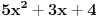 nam je OK, a polinom 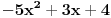 nije OK). Drugo, taj polinom treba da bude nesvodljiv: to znači da se ne može napisati kao proizvod nekih polinoma manjeg stepena (znači, polinom 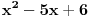 nije OK, jer ga možemo zapisati kao 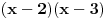 ; s druge strane, polinom, primera radi, 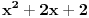 jeste OK, jer ga nikako ne možemo zapisati kao proizvod nekih polinoma manjeg stepena). Postoji i još jedan uslov, ali lakše mi je da njega uvedem malo kasnije. Onda H-hipoteza tvrdi da za beskonačno mnogo prirodnih brojeva  vrednost 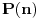 jeste prost broj. Recimo, jedan specijalan slučaj je tvrđenje da postoji beskonačno mnogo prostih brojeva 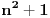 (ovo dobijamo kada za pominjani polinom uzmemo 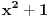 , što ispunjava sve tražene uslove).
Što se samih uslova tiče, oni su vrlo prirodni jer je jasno da bez njih ne možemo: primeti da, ako bismo dopustili i polinome s negativnim vodećim koeficijentimo (recimo, pomenuti 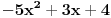 , tada će ovaj polinom za sve  od nekog momenta nadalje uzimati negativne vrednosti, pa je jasno da se tu nećemo previše 'leba najesti od prostih brojeva. Smisao drugog uslova takođe nije teško dokučiti: ako je, recimo, 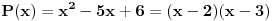 , tada koji god broj  ubacimo u ovaj polinom, dobićemo vrednost 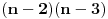 , a što već za 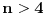 nikada nije prost prost broj jer je predstavljeno kao proizvod dva broja oba veća od  .
E sad, ako si ovo sve ukapirao, to nije kraj pošto smo sve ovo pričali preko samo jednog polinoma, ali H-hipoteza je formulisana i kada imamo koliko god polinoma, a ne samo jedan. Dakle, neka su 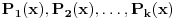 polinomi od kojih svaki ispunjava uslove koje smo nabrajali. Uz to, dodajmo i onaj treći uslov koji sam maločas pomenuo; citiraću ga najpre onako kako sam napisao i u prethodnoj poruci, a onda ćemo tumačiti šta to znači: „ni za jedan prost broj  nije ispunjeno da za svaki prirodan broj  broj  deli neku od vrednosti 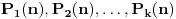 “. Hajde da se udubimo u ovo. Neka su dati polinomi 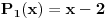 i 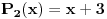 . Primetimo sada da, za ma koji prirodan broj  , jedna od vrednosti 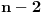 i 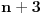 sigurno je parna, tj. deljiva sa  . Drugim rečima, za prost broj  ispunjeno je da, ma koji prirodan broj  da ubacimo u odabrane polinome, broj  deliće neku od vrednosti 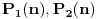 . Dakle, ovaj par polinoma nije u skladu s postavljenim uslovom (uslov kaže da ni za jedan prost broj  ne sme da se desi ono iz nastavka rečenice, a nama se to desilo za 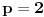 ). Isto tako, ne sme se desiti da je uvek neki od brojeva 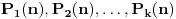 deljiv sa  (recimo, ako uzmemo tri polinoma: 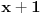 , 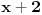 i 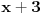 , oni krše postavljeni uslov), pa isto to za  , pa isto to za 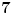 ... E, konačno, H-hipoteza tvrdi da, kakvu god gomilu polinoma da imamo (ali da oni ispunjavaju zahteve koje smo naveli), onda postoji beskonačno mnogo prirodnih brojeva  za koje su brojevi 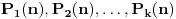 svi istovremeno prosti.
I sad ako uzmeš npr. polinome 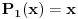 i 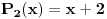 , tada se tvrdi da postoji beskonačno mnogo prirodnih brojeva  takvih da su i broj  i broj 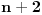 ujedno prosti, a ovo je upravo hipoteza o prostim blizancima.
Citat: Nedeljko:
Bojane, da li ti primećuješ nerazumevanje materije od strane učesnika? Ako je odgovor pozitivan, pomozi im.
Evo, trudim se, nadam se da će sad biti uspešnije. 
Citat: number42:
a ovo bi moglo i da se uopsti, tako da bi izvedena hipoteza bila:
"izmedju bilo kog broja n i njegove dvostruke vrednosti 2n uvek je smesten barem jedan prost broj".
Ovo postoji i dokazano je. Potraži pod nazivom Bertranov postulat (negde se sreće i naziv Čebiševljeva teorema). [ number42 @ 03.06.2013. 00:32 ] @
ej bre, nisi se morao truditi, reko sam ti ako te mrzi ne moras objasnjavati.
ovo si bas detaljno i opsirno objasnio i potrudio se, a verujem da mi treba jos primera (koje cu naci na wiki) da u potpunosti ukapiram.
a inace, pre cu sam nesto ukapirati nego kad mi neko objasnjava, uvek sam tako radio iz matematike 
nije stvar u tebi nego ja kapiram na svoj nacin i to je to.
a i ova me oblast bas zanima pa bih mogao i malo detalnije da je prelistam na netu.
inace bas si me iznenadio da je hipoteza "izmedju bilo kog broja n i njegova dvostruke vrednosti 2n se uvek nalazi bar jedan prost broj" dokazana.
ova hipoteza dikretkno proizilazi iz goldbahove, i njen dokaz bi trebalo da znaci da je i goldbahova delom dokazana. definitivno ce da pogledam.
______________
takodje, potreno mi je jedno par dana da ukapiram kakav sam seljak  evo naknadno sam video da je hipoteza koju sam dao u startu na pocetku- samo izvedena iz druge hipoteze kojoj tada nisam znao ime.
jer, ako se "svako 2n moze napisati kao razlika nekih Pb1 i Pb2", onda se matematickom radnjom na nivou treceg osnovne dolazi do hipoteze iz prvog posta:
svako 2n=neki Pb1 - neki Pb2
svako 2n + neki Pb2=neki Pb1
iz ovoga direktno sledi:
1+svaki Pb1+neki Pbx= neki Pb2
dakle darkosos je bio u pravu da je ovo samo specijalan slucaj.
____________
nego, zanima me sledece:
da li je glupo da pretpostavim sledece:
neki Pb1- neki Pb2= neki Pb3 - neki Pb4
ovo bi prakticno znacilo da gep izmedju bilo koja dva prosta broja ne moze biti jedinstven, vec se ponavlja beskonacno mnogo puta. ne mislim na uzastopne nego bilo koje.
npr 101 - 3 = 98
postoji beskonacno mnogo parova prostih brojeva sa gepom 98
23 - 13 = 10
posoji beskonacno mnogo parova prostih brojeva sa gepom 10
itd.
nekako mi izgleda da bilo koju hipotezu koju postavis za proste mozes postaviti i za slozene. kao da su slozeni izuzeci, a ne obrnuto.
EDIT: dodao sam 'neki' uz 'Pb4'
EDIT 2: lapsus, zamenio 'prost' umesto 'parni'
[Ovu poruku je menjao number42 dana 03.06.2013. u 02:13 GMT+1]
[Ovu poruku je menjao number42 dana 03.06.2013. u 02:41 GMT+1][ number42 @ 03.06.2013. 04:03 ] @
evo skontao sam ovu h-hipotezu, ali mi bas nesto i nema smisla.
znaci, imamo gomilu nekih brojeva.
uslovi su- da iz te gomile brojeva:
-nijedan ne sme biti negativan
-nijedan ne sme biti slozen
-nijedan ne sme biti deljiv sa nekim prostim brojem
a zakljucak je hipoteza: da su onda svi ti brojevi iz gomile prosti...
pa u cemu je fora? vidi se jasno iz uslova.
[ Nedeljko @ 03.06.2013. 10:22 ] @
Ne, nisi razumeo.
Evo, na primer, polinom 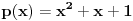 spunjava navedene uslove.
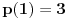 ,
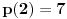 ,
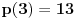 ,
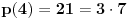 .
Dakle, nije tačno da su svi brojevi oblika 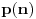 gde je  prirodan broj prosti, već da prirodnih brojeva tog oblika ima beskonačno mnogo. Polinom  nije rastavljiv na proizvod dva polinoma nižeg stepena, ali to ne znači da za neki prirodan broj  broj 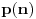 ne može biti proizvod dva manja prirodna broja.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|