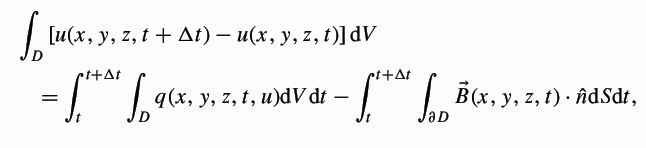Van konteksta? Tesko.

Inace, mislim da je ovo pitanje vise za fizicare.

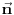
Prvo je integral po prostoru, drugo su dva uzastopna integrala, prvo po prostoru, pa onda po vremenu, a treće su opet dva uzastopna, prvo površinski po granici druge vrste ( je jedinična normala na granicu), ako smatramo tu normalu delom elementa integracije, odnosno prve vrste ako je smatramo delom podintegralne funkcije (svejedno je, rezultat je isti). Verovatno je veza između drugog i trećeg Stoksova formula, ali naravno fali kontekst svih oznaka pod integralima.

Formula mi nije poznata, ali izgleda kao da pokušava da se pokaže da je nešto (u???) u nekom delu prostora posledica promene količine naelektrisanja i magnetne indukcije.

Nije mi jasno kako je dobiveno i ?

_{[Ovu poruku je menjao R A V E N dana 02.06.2013. u 21:33 GMT+1]}

Eto, postavio sam prateći tekst, pa se nadam da će sada biti jasnije.

Je li može moderator ovo prebaciti u forum Fizika?

Rekao bih da formula govori da je promjena u količini toplote (toplotne energije) u nekom tijelu u toku nekog vremenskog intervala, jednaka razlici količine toplote koja se u tom vremenskom intervalu unutar tog tijela proizvede i toplote koja se iz tijela za taj isti interval vremena izrači.

To je i logično: do promjene količine toplote može doći samo tako što je ili odnekle dobijaš ili nekud gubiš. Razlika između to dvoje ti govori kolika je promjena.