Za ovaj drugi: pretvori proizvod u zbir, trerbalo bi da se pojednostavi...

Hvala za hint. Pokusacu.
Evo pokusaja za arcuse. Ali na kraju mi se interval ne slaze tj, nije odgovarajuci



ps.: Izvinjavam se, nemam vremena da prekucavam u TeX

Mislim da si uradila dobro, rezultat je

Ali fazon je sto mi ne upada u domen za arc. Ne znam koliko je ovo ovako korektno.

Evo resenja za pitanje 2. Reci mi jel OK.



Opet slika, izvinjavam se

Ako nije tajna, kako dolazis do tog rezultata?

Što se prvog tiče, neka je . To znači da je

,
,
.

Ukoliko je , važi

,
.

Poslednje sledi na osnovu formule koja joj prethodi i poređenja znaka leve i desne strane ove jednakosti jer u slučaju važi i , dok u slučaju važi i .



Dakle,

,
.

Dakle, zbir tih arkuskosinusa je .

Edit: Hvala, Sonec.

_{[Ovu poruku je menjao Nedeljko dana 03.06.2013. u 01:08 GMT+1]}

Nedeljko, fali ti minus kod druge primene izvedene formule. Tako da je Darkovo resenje ipak blize (kompaktnije, kako je kome drago).

Hvala.

Tajna je :) Elem, jesam ostao duzan za objasnjenje, ali to je zato sto sam samo proverio rezultat; ali evo sada i objasnjenja - koje se svodi na to da tako ne treba raditi :) ...

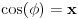
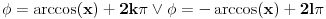
Kao sto je poznato, ako je , onda je , gde su k i l proizvoljni celi brojevi.

Ovo svakako ne izgleda kao dobra osnova za tacno odredjivanje ugla, jer imamo posla sa dve vrste intervala i dve vrste resenja:

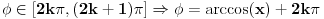
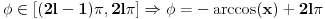
i , sto se dobija kada se u gornja resenja stavi interval u kome se nalazi arccos, .

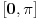
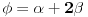
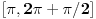
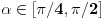
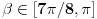
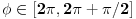
U ovom konkretnom slucaju, imas da pripada intervalu , sto je ocigledno previse gruba procena da bi mogla da se iskoriste navedena pravila. Zato nam treba bolja procena, pa bi uz malo mozganja mogli da zakljucimo da je i , pa je , sto konacno daje rezultat koji sam dao u prethodnoj poruci.

Sve u svemu, ocaj... Dakle ovaj pristup nije previse dobar, prvo imas mnogo posla oko odredjivanja svih sinusa i kosinusa, a drugo, imas problem odredjivanja intervala u kome se zbir uglova nalazi. Tako da je resenje sa svodjenjem na arctan, koje je Nedeljko dao, mnogo operativnije; glavni razlog je to sto tangens nema ova dvojaka resenja i mnogo lakse se odredjuje gde je tacno ugao. To sto je ispalo da se drugi arctan moze svesti na prvi je samo bonus, sto je dozvolilo da nam procena zbira uglova uopste i ne treba... Jedina mana je sto se koriste neke manje poznate formule, ali ocigledno da ih vredi nauciti.

Prednost pristupa sa arkustangensom je što se u formuli za tangens zbira uglova pojavljuje samo tangens, a ne kao u formulama za sinus odnosno kosinus zbira uglova, gde se pojavljuju i sinus i kosinus.

,

Pretpostavimo da je . U tom slučaju je

,

pa postoji konstanta takva da je

.

Dakle, funkcija



je definisana za svako za koje je , neprekidna je i vrednost u bilo kojoj tački joj je celobrojan umnožak broja . Stoga je ona konstantna na svakoj komponenti povezanosti domena. Jedna od komponenti povezanosti je . Dovoljno je odrediti vrednost funkcije u bar jednoj tački te oblasti jer je funkcija na njoj konstantna. Obzirom da je , zaključujemo da je

za .

Preostale dve oblasti su i . Vrednost funkcije na prvoj možemo odrediti puštajući da , a na dugoj puštajući da . Rezultat je da je na prvoj oblasti vrednost funkcije , a na drugoj . Stoga je

za , ,
za , .

Lako je dokazati da je

za , ,
za , .

_{[Ovu poruku je menjao Nedeljko dana 04.06.2013. u 14:57 GMT+1]}

Ovaj odgovor me inspirisao da probam ovako:

Prvo iskoristiti da je a onda dva puta primeniti formulu za x,y > 0.

Moguce da nesto nije bas svuda tako, odnosno da nedostaju neki uslovi (ovo za x,y > 0 je vise intuitivno), ali dobio sam trazeni rezultat...
Dakle, da bude jasnije, racunao sam .