kako se u latexu pise 'svaki' i 'neki', ono izvrnuto A i i zvrnuto E?

hteo sam ceo zadatk da napisem samo pomocu simbola, ali mi se ne da.
na celoj temi o latexu nema nista o tome, a ne pomaze ni wolfram, ni wiki...

\forall ->
\exists ->

hvala atomski mrave. sacu umetnem.

To tvrđenje se može oboriti. Recimo, može se dokazati da za traženi brojevi i ne postoje.

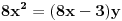
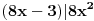
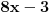
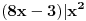
U suprotnom važi , odnosno . Pošto su i uzajamno prosti (prvi je stepen prostog broja 2, a drugi nije deljiv njime), odatle sledi da , odnosno postoji prirodan broj takav da je

,
.

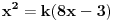
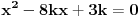
Da bi poslednja kvadratna jednačina imala celobrojna rešenja, diskriminanta joj mora biti potpun kvadrat. Dakle, za neko važi

.

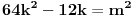
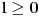
Leva strana je deljiva sa 4, pa mora biti i desna, odnosno mora biti paran broj, pa za neko važi

,
,
.

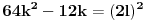
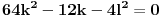
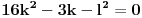
Da bi ova jednačina imala makar i racionalno rešenje (jer ako nema racionalnog, nema ni celobrojnog) diskriminanta mora biti potpun kvadrat, tj. za neko važi.

.

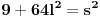
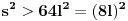
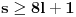
Obzirom da je , važi , a pošto radimo sa celim brojevima, to znači da je , pa je

,
,
,
,
.

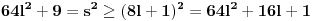
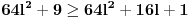
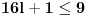
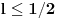
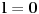
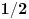
Ovo poslednje zato što je ceo nenegativan broj ne veći od . No, to dalje znači da je

,
.

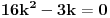
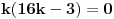
Obzirom da ova jednačina nema rešenja u skupu prirodnih brojeva, dobili smo kontradikciju.

moze lock teme. pogresna postavka. izvinjavam se svima.