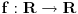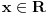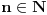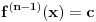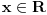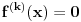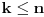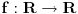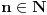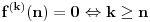[ Sonec @ 07.06.2013. 22:50 ] @
|
[ Nedeljko @ 08.06.2013. 19:29 ] @
Pretpostavimo suprotno, da funkcija
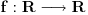 nije polinomska, ali da važi nije polinomska, ali da važi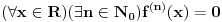 . .1 . 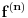 je neprekidno. je neprekidno.Dokaz: Neprekidno je kao diferencijabilno jer postoji 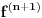 . .2. Oznaka: 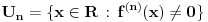 . .3. Skup  svih tačaka koje imaju okolinu na kojoj je funkcija svih tačaka koje imaju okolinu na kojoj je funkcija  polinomijalna je otvoren i svuda gust i na njemu je funkcija lokalno polinomijalna. polinomijalna je otvoren i svuda gust i na njemu je funkcija lokalno polinomijalna.Dokaz: Netrivijalno je dokazati da je skup  svuda gust. Obzirom da je svuda gust. Obzirom da je 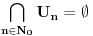 i da su skupovi i da su skupovi 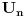 otvoreni, po Berovoj teoremi za svaki pravi interval otvoreni, po Berovoj teoremi za svaki pravi interval  postoji postoji 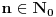 takvo da takvo da 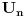 nije gust u nije gust u  , odnosno postoji pravi interval , odnosno postoji pravi interval 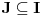 takav da je takav da je 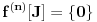 . No, to znači da je . No, to znači da je  polinomijalna na intervalu polinomijalna na intervalu  . Za ma koje . Za ma koje 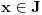 važi važi 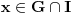 . .4. Oznaka:  je niz disjunktnih otvorenih intervala čija je unija skup je niz disjunktnih otvorenih intervala čija je unija skup  . .5. Oznaka: 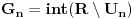 - skup tačaka koje imaju okolinu u kojoj je funkcija polinomijalna stepena manjeg od - skup tačaka koje imaju okolinu u kojoj je funkcija polinomijalna stepena manjeg od  , ,6. Oznaka: 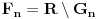 , ,7. Oznaka: 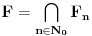 . .8. Skup  je zatvoren, je zatvoren,Dokaz: Na osnovu 1. 9. 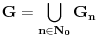 . .10. Ako je funkcija na pravom intervalu polinomijalna, taj polinom je jednoznačno određen. Dokaz: Polinom je jednoznačno određen vrednostima u bilo kojih beskonačno mnogo tačaka. 11. Neka je  bilo koji pravi otvoreni interval na kome je funkcija bilo koji pravi otvoreni interval na kome je funkcija  lokalno polinomijalna. Ona je na njemu polinomijalna. lokalno polinomijalna. Ona je na njemu polinomijalna.Dokaz: Za ma koji kompaktan interval 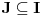 ma koja tačka ma koja tačka 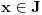 ima okolinu u kojoj je funkcija ima okolinu u kojoj je funkcija  polinomijalna. Takve okoline čine otvoreni pokrivač kompaktnog skupa polinomijalna. Takve okoline čine otvoreni pokrivač kompaktnog skupa  . Iz njega možemo izdvojiti konačan potpokrivač. Obzirom da je na svakom elementu konačnog potpokrivača funkcija . Iz njega možemo izdvojiti konačan potpokrivač. Obzirom da je na svakom elementu konačnog potpokrivača funkcija  polinomijalna, možemo uočiti prirodan broj polinomijalna, možemo uočiti prirodan broj  koji je veći od stepena svih tih konačno mnogo polinoma, pa na kompaktu koji je veći od stepena svih tih konačno mnogo polinoma, pa na kompaktu  važi važi 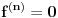 , pa je na unutrašnjosti intervala , pa je na unutrašnjosti intervala  funkcija funkcija  polinomijalna. Neka je polinomijalna. Neka je 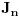 rastući niz kompaktnih podintervala od rastući niz kompaktnih podintervala od  takvih da je unija njihovih unutrašnjosti interval takvih da je unija njihovih unutrašnjosti interval  . Funkcija . Funkcija  je polinomijalna na svakom od njih, a prema 10 su svi ti polinomi jednoznačno određeni vrednošću funkcije na je polinomijalna na svakom od njih, a prema 10 su svi ti polinomi jednoznačno određeni vrednošću funkcije na 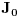 , pa se radi o jednom polinomu. Stoga je funkcija , pa se radi o jednom polinomu. Stoga je funkcija  polinomijalna na celom intervalu polinomijalna na celom intervalu  . .12. Funkcija  je polinomijalna na svakom od intervala je polinomijalna na svakom od intervala  . .Dokaz: Na osnovu 11. 13. Izvodi funkcije  bilo kog reda na bilo kom kraju intervala bilo kog reda na bilo kom kraju intervala  jednaki su odgovarajućim izvodima na tom kraju intervala jednaki su odgovarajućim izvodima na tom kraju intervala  polinoma kome je funkcija polinoma kome je funkcija  jednaka na intervalu jednaka na intervalu  . .Dokaz: Na osnovu 1. 14. Tejlorov razvoj funkcije u okolini bilo kog od krajeva intervala  je konačan i jednak funkciji je konačan i jednak funkciji  na intervalu na intervalu  . .Dokaz: Sledi iz 13 i osobina polinoma. 15: Ako je funkcija  polinomijalna na dva intervala koji imaju jedan zajednički kraj, onda je polinomijalna i na uniji zatvorenja tih intervala. Opštije, ako je funkcija polinomijalna na dva intervala koji imaju jedan zajednički kraj, onda je polinomijalna i na uniji zatvorenja tih intervala. Opštije, ako je funkcija  lokalno polinomijalna na nekom intervalu bez nekog diskretnog skupa tačaka, onda je polinomijalna na zatvorenju tog intervala. Stoga intervala lokalno polinomijalna na nekom intervalu bez nekog diskretnog skupa tačaka, onda je polinomijalna na zatvorenju tog intervala. Stoga intervala  ima beskonačno mnogo. ima beskonačno mnogo.Dokaz: Sledi iz 14. 16: Svaki od krajeva intervala  pripada skupu pripada skupu  . .Dokaz: U suprotnom postoji okolina  tog kraja u kojoj je funkcija tog kraja u kojoj je funkcija  polinomijalna, pa je polinomijalna, pa je 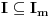 za neko za neko  . No, u tom slučaju je . No, u tom slučaju je 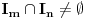 suprotno izboru tih intervala. suprotno izboru tih intervala.17: Skup  nema izolovanih tačaka. nema izolovanih tačaka.Dokaz: Ako je  izolovana tačka skupa izolovana tačka skupa  , postoji , postoji  takvo da je takvo da je 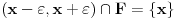 . Obzirom da je funkcija . Obzirom da je funkcija  lokalno polinomijalna na lokalno polinomijalna na 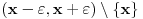 ona je prema 15 polinomijana na ona je prema 15 polinomijana na 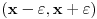 , što protivreči izboru tačke , što protivreči izboru tačke  . .18: Neka je  otvoren skup takav da je otvoren skup takav da je 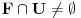 i neka je prirodan broj i neka je prirodan broj  . Postoji tačka . Postoji tačka 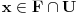 takva da je takva da je 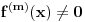 . .Dokaz: U skupu  možemo izabrati neki od intervala možemo izabrati neki od intervala  na kome se na kome se 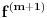 ne anulira. U suprotnom, pošto je na osnovu 3 skup ne anulira. U suprotnom, pošto je na osnovu 3 skup 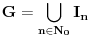 svuda gust, na osnovu neprekidnosti svuda gust, na osnovu neprekidnosti 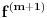 je je 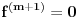 na celom skupu na celom skupu  , što je u suprotnosti sa , što je u suprotnosti sa 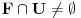 . Za tako izabrani . Za tako izabrani  neka je neka je  stepen polinoma kome je funkcija stepen polinoma kome je funkcija  jednaka na intervalu jednaka na intervalu  . Obzirom da se . Obzirom da se 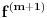 ne anulira na tom intervalu, važi ne anulira na tom intervalu, važi  . Obzirom da je . Obzirom da je 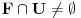 , interval , interval  se ne svodi na se ne svodi na  , pa mu barem jedan od krajeva pripada skupu , pa mu barem jedan od krajeva pripada skupu  . Obeležimo ga sa . Obeležimo ga sa  . Ukoliko je . Ukoliko je 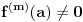 tvrđenje je dokazano (jer tvrđenje je dokazano (jer 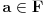 na osnovu 16). Pretpostavimo zato da je na osnovu 16). Pretpostavimo zato da je 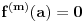 . Svakako je . Svakako je 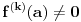 . Neka je . Neka je  najmanji broj iz skupa najmanji broj iz skupa 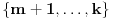 takav da je takav da je 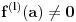 . Izaberimo okolinu . Izaberimo okolinu 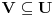 tačke tačke  takvu da je takvu da je 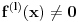 . To je moguće na osnovu 1. Obzirom da je za . To je moguće na osnovu 1. Obzirom da je za 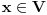 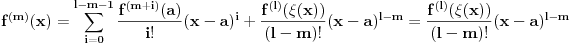 za neko 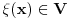 , važi , važi 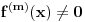 za sve za sve 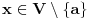 . Obzirom na 17 i . Obzirom na 17 i 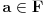 , tvrđenje sledi. , tvrđenje sledi.19: 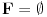 . .Dokaz: Pretpostavimo da je 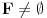 . Prema 18, obzirom da je . Prema 18, obzirom da je 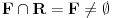 , možemo izabrati tačku , možemo izabrati tačku 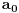 skupa skupa 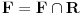 za koju je za koju je 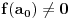 i na osnovu neprekidnosti i na osnovu neprekidnosti  kompaktnu okolinu kompaktnu okolinu 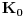 takvu da takvu da 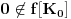 . Obzirom da je . Obzirom da je 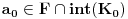 u okolini u okolini 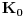 možemo izabrati unutrašnju tačku možemo izabrati unutrašnju tačku 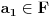 takvu da je takvu da je 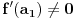 i na osnovu neprekidnosti i na osnovu neprekidnosti 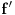 kompaktnu okolinu kompaktnu okolinu 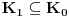 takvu da takvu da 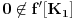 . Nastavljajući ovaj postupak, konstruišemo opadajući niz . Nastavljajući ovaj postupak, konstruišemo opadajući niz 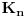 kompakata takav da kompakata takav da 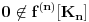 . Za . Za 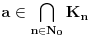 je je 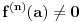 za sve za sve 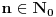 suprotno pretpostavci zadatka. suprotno pretpostavci zadatka.20.  je lokalno polinomijalna na je lokalno polinomijalna na  . .Dokaz: Na osnovu 19 je 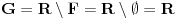 . .21.  je polinomijalna na je polinomijalna na  suprotno pretpostavci. suprotno pretpostavci.Dokaz: Na osnovu 11 i 20. [Ovu poruku je menjao Nedeljko dana 09.06.2013. u 01:06 GMT+1] [ Nedeljko @ 08.06.2013. 22:07 ] @
Sonec,
ako ti nije mrsko, daj neki hint, jer sumnjam da je moje rešenje najelegantnije. [ zzzz @ 09.06.2013. 00:17 ] @
[ Nedeljko @ 09.06.2013. 09:35 ] @
[ zzzz @ 09.06.2013. 21:48 ] @
Citat: Ovdje ne piše da n-ti izvod nesmije biti nula na cijelom R.A traži se dokaz da je ta funkcija polinom,što nije teško.Dokažimo i da nemože biti nešto drugo osim polinoma. Ako razmotrimo i takav slučaj tj. da izvedene funkcije prave ogroman broj nula i da je n ogroman broj to ni slučajno neće pokriti sve x-ove na R. Može se dokazati uslovom derivabilnosti. [ Nedeljko @ 09.06.2013. 22:24 ] @
Citat: zzzz: Ovdje ne piše da n-ti izvod nesmije biti nula na cijelom R. Tačno. Isto tako ne piše ni da n-ti izvod mora biti nula na celom R. Možeš koristiiti samo ono što je dato u zadatku. Citat: zzzz: A traži se dokaz da je ta funkcija polinom,što nije teško.Dokažimo i da nemože biti nešto drugo osim polinoma. Kako? Citat: zzzz: Ako razmotrimo i takav slučaj tj. da izvedene funkcije prave ogroman broj nula i da je n ogroman broj to ni slučajno neće pokriti sve x-ove na R. Može se dokazati uslovom derivabilnosti. Ako izvodi beskonačno diferencijabilne funkcije prave sve više nula, zaista sve one ne moraju pokriti ceo R. Međutim, uslov zadatka je da za svaku tačku postoji izvod nekog reda koji se anulira u toj tački. Uz taj uslov nema kontraprimera. Upravo sam to dokazao. Ako misliš da kontraprimera ima, slobodno ga konstruiši. [ darkosos @ 10.06.2013. 08:54 ] @
Nasao sam neke dokaze na net-u, i u principu to jeste put kojim je Nedeljko isao. Ipak sam se iznenadio da je potreban tako fundamentalan dokaz za nesto sto izgleda "ocigledno". Inace, razmisljajuci o ovom problemu, mislio sam da nesto moze da se uradi preko Tejlorovog razvoja. Rekao bih da na osnovu datih uslova nije tesko zakljuciti da je Tejlorov polinom ovakve funkcije u svakoj tacki bez ostatka, tj. da je postoji razvoj bez ostatka. Dalje bi trebalo pokazati da je ovakva osobina lokalna, tj. da za svaku tacku postoji okolina u kojoj je funkcija jednaka svom Tejlorovom polinomu - ovo verovatno i predstavlja najveci izazov, sudeci po izlozenom dokazu. Mislio sam da nesto moze da se uradi sa Lagranzevim ostatkom - on se u ovom slucaju uvek moze svesti na 0. Na kraju bi se iskoristio argument da lokalno polinomska funkcija jeste polinom. U svakom slucaju, to je skica koju sam imao u glavi, i ne sumnjam da dokaz moze i tako da se izvede, s' obzirom da je tvrdjenje tacno - osim, naravno, ako neki od argumenata koje sam izneo nisu valjani :)
[ Nedeljko @ 10.06.2013. 09:27 ] @
Ja zaista ne znam kako bi se dokazalo da Tejlorov razvoj ove funkcije u okolini bilo koje tačke konvergira funkciji u barem jednoj okolini te tačke, tj. da je funkcija analitička. To nije opšte svojstvo beskonačno diferencijalnih funkcija. Postoji čuveni primer funkcije
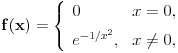 . .koja je beskonačno diferencijabilna na celom skupu realnih brojeva, a Tejlorov razvoj u okolini nule joj se svodi na nulu ( 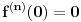 za sve za sve 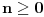 ), što se svakako razlikuje od vrednosti funkcije u bilo kojoj drugoj tački. ), što se svakako razlikuje od vrednosti funkcije u bilo kojoj drugoj tački.Naravno, obzirom da iz navedenih uslova sledi da je funkcija polinmijalna, ona je svakako analitička sa konačnim Tejlorovim razvojem u svakoj tački, ali ja ne znam kako bih dokazao da je funkcija analitička bez da znam da je polinomijalna, tj. kako bih tim putem (preko dokaza analitičnosti) dokazao polinomijalnost funkcije. [ Nedeljko @ 10.06.2013. 09:28 ] @
Nego, postavljač teme se nešto ućutao. Baš me zanima koje je rešenje predvideo. Ne mora celo, ali barem neka da hint.
[ darkosos @ 10.06.2013. 10:17 ] @
@Nedeljko
Ne znam ni ja, zato sam i stao :) Nego, funkcija koju si naveo ne zadovoljava naravno uslove zadatka, za x <> 0. Tako da ima tu nesto... Ono sto sam se pitao, zaboravio sam ako sam i znao, je gde vazi recimo formula Lagranzovog ostatka? Mislim na procenu greske 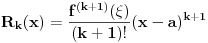 ? Rekao bih da ona mora da vazi u nekoj okolini tacke u kojoj se trazi razvoj... Ako je to tako, onda bi bilo ? Rekao bih da ona mora da vazi u nekoj okolini tacke u kojoj se trazi razvoj... Ako je to tako, onda bi bilo 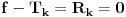 u nekoj okolini bilo koje tacke. Ili ja nesto grdno gresim :) u nekoj okolini bilo koje tacke. Ili ja nesto grdno gresim :)[ Nedeljko @ 10.06.2013. 10:28 ] @
Uslove zadatka ispunjavaju samo polinomi, ali to treba dokazati.
Lagranžev oblik ostatka važi u opštem slučaju. Još "samo" kada bi dokazao da za dato  postoje postoje 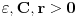 tako da za svako tako da za svako 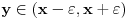 važi važi 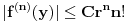 za beskonačno mnogo prirodnh brojeva za beskonačno mnogo prirodnh brojeva  , bio bi na konju. No, to za beskonačno diferencijabilne funkcije u opštem slučaju nija tačno. Ništa ti ne znači Lagranžev oblik Tejlorovog ostatka ako nemaš nikakvu procenu izvoda proizvoljnog reda u bar jednoj okolini. , bio bi na konju. No, to za beskonačno diferencijabilne funkcije u opštem slučaju nija tačno. Ništa ti ne znači Lagranžev oblik Tejlorovog ostatka ako nemaš nikakvu procenu izvoda proizvoljnog reda u bar jednoj okolini.[ darkosos @ 10.06.2013. 10:51 ] @
[ Nedeljko @ 10.06.2013. 10:57 ] @
[ darkosos @ 10.06.2013. 11:06 ] @
Tako sam i mislio, tu znaci sada nedostaje korak u kojem bi se iskoristilo to da za svako x ima neko n u kojem je n-ti izvod 0, pa znaci treba pokazati da potoji taj najveci red izvoda u okolini tacke, za koji su izvodi u svim tackama te okoline jednaki nuli. Tako bi i to
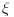 , koje mora biti iz te okoline, zadovoljavalo isti uslov... , koje mora biti iz te okoline, zadovoljavalo isti uslov...[ Nedeljko @ 10.06.2013. 11:20 ] @
Pa, mislim, fali. Slažem se. Pokušavao sam ja na te fore preko funkcionalne analize, ali je problem sa primenom bio što operator diferenciranja nije ograničen, već samo zatvoren, što mi nije bilo dovoljno.
[ Sonec @ 10.06.2013. 15:20 ] @
Ja sam u velikoj guzvi ovih dana tako da ne zamerite na mom neucestovavanju u temi (sto ce se i nastaviti bar jos 5,6 dana).
Nedeljko je trazio neki hint i evo nekih smernica (mozda je previse detaljno, al ja ne mogu sada da ga redukujem): - Neka je 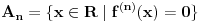 i i 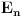 interior od interior od 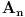 . Pokazati da je . Pokazati da je 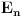 neprazan neprazan- Pokazati da je 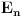 prebrojiva unija otvorenih segmenata prebrojiva unija otvorenih segmenata- Primetiti da je dovoljno pokazati da je 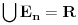 - Neka je 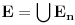 i i  komplement od komplement od  . Pokazati da postoji interval . Pokazati da postoji interval  takav da je takav da je 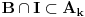 i i 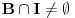 -  nema izolovanih tacaka nema izolovanih tacaka- Po konstrukciji 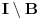 je unija intervala koji se pojavljuju u nekom je unija intervala koji se pojavljuju u nekom 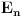 . Uzimimo takav jedan interval . Uzimimo takav jedan interval  , recimo , recimo 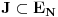 (gde je (gde je  minimalno) i neka je minimalno) i neka je  jedan kraj intervala jedan kraj intervala  . Pokazati . Pokazati 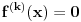 , stavise, , stavise, 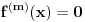 za za 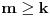 .Zatim pokazati .Zatim pokazati 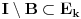 , sto nas dovodi u kontradikciju. , sto nas dovodi u kontradikciju.[ Bojan Basic @ 10.06.2013. 16:31 ] @
Čini mi se da se Nedeljkova ideja može malo skratiti. Koristiću Nedeljkove oznake, osim
 i i  , što kod mene označava nešto drugo. , što kod mene označava nešto drugo.Primenićemo Berovu teoremu ne na prostor 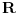 , nego na njegov potprostor indukovan skupom , nego na njegov potprostor indukovan skupom 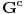 (ovaj skup je zatvoren, pa je posmatrani potprostor takođe kompletan metrički prostor). Kako je (ovaj skup je zatvoren, pa je posmatrani potprostor takođe kompletan metrički prostor). Kako je 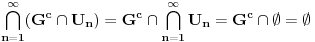 , iz Berove teoreme dobijamo postojanje otvorenog intervala , iz Berove teoreme dobijamo postojanje otvorenog intervala  takvog da je skup takvog da je skup 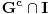 neprazan i disjunktan sa neprazan i disjunktan sa 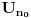 za neko za neko 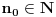 , tj. da važi , tj. da važi 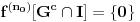 . Kako skup . Kako skup 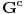 nema izolovanih tačaka, svaka tačka skupa nema izolovanih tačaka, svaka tačka skupa 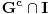 jeste tačka nagomilavanja, odakle (zbog beskonačne diferencijabilnosti) sledi jeste tačka nagomilavanja, odakle (zbog beskonačne diferencijabilnosti) sledi 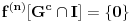 za sve za sve  . Dalje, neka je . Dalje, neka je 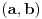 ma koji maksimalan otvoren podinterval otvorenog skupa ma koji maksimalan otvoren podinterval otvorenog skupa 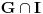 . Funkcija . Funkcija  jeste polinom na intervalu jeste polinom na intervalu 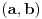 (recimo, prema Nedeljkovom koraku 11), pa je za neko (recimo, prema Nedeljkovom koraku 11), pa je za neko  funkcija funkcija 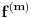 jednaka nenula konstanti na intervalu jednaka nenula konstanti na intervalu 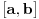 (prelazan na zatvoren interval vršimo zahvaljujući neprekidnosti). No, kako nije teško primetiti da bar jedna od tačaka (prelazan na zatvoren interval vršimo zahvaljujući neprekidnosti). No, kako nije teško primetiti da bar jedna od tačaka  ili ili  mora pripadati skupu mora pripadati skupu 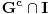 , dobijamo , dobijamo 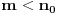 , te je , te je 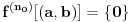 . Odatle je, sveukupno, . Odatle je, sveukupno, 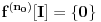 , ali ovo je u kontradikciji s činjenicom da je skup , ali ovo je u kontradikciji s činjenicom da je skup 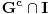 neprazan. neprazan.[ zzzz @ 10.06.2013. 17:15 ] @
Ja bih to probao jednostavnije.Neka ta funkcija nije polinom, i ima izvode,prvi,drugi,treći itd koliko hoćeš.Neka za svaki x bar jedna od tih izvedenih funkcija ima nulu.
Formirajmo novu funkciju tako da pomnožimo sve izvode početne funkcije. 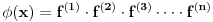 Pošto je bar jedan faktor za bilo koji x nula onda će cijela funkcija biti nula za svako x,pa i njen izvod takođe za svako iks je nula. Napravimo prvi izvod te funkcije (koji će morati biti jednak nuli) i posmatrajmo samo onaj najintresantniji član za željeni x.Ispada da će izvod od izvoda koji je za taj x imao nulu morati opet imati nulu na istom mjestu. 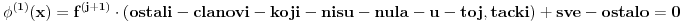 ,(Ono sve-ostalo je nula u toj tački zbog j-tog izvoda.Ja mislim da je dokazivo?Takođe i ako u datoj tački ima dvije ili više funkcija izvoda kojima je to nula.Da ne smaramo ako nije potrebno.) ,(Ono sve-ostalo je nula u toj tački zbog j-tog izvoda.Ja mislim da je dokazivo?Takođe i ako u datoj tački ima dvije ili više funkcija izvoda kojima je to nula.Da ne smaramo ako nije potrebno.)Zaključak:Ako u nekoj tački imamo nulu j-tog izvoda,onda će i svi naredni izvodi imati nulu u toj tački.Dalje je lako dotjerati do polinoma kao jedine mogućnosti. [ Nedeljko @ 10.06.2013. 18:32 ] @
Citat: Ovde se množi konačno mnogo izvoda funkcije, a ne svi izvodi (jer njih ima beskonačno mnogo), tako da navedena rečenica nije u skladu sa formulom. Ako bi pak izmnožio sve izvode, to je beskonačan proizvod, pa bi morao da dokažeš konvergenciju. Čak i kada bi je dokazao, morao bi da dokažeš da se može formalno diferencirati član po član. [ zzzz @ 11.06.2013. 09:06 ] @
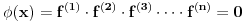 (ako postoji,i u skladu sa zahtjevom zadatka) Uočimo izvod najnižeg reda koji siječe osu x,neka je to naprimjer prvi izvod. Prvi izvod gornje funkcije možemo napisati: 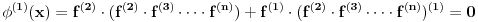 Slijedi zaključak da je i drugi izvod jednak nuli za istu tačku jer svi ostali izvodi nisu jednaki nuli u toj tački. Možemo odabrati bilo koji x i naći koji izvod tu ima nulu.Istim načinom dokazali bi da i izvod tog izvoda,dakle sledeći takođe tu mora imati nulu. Uzmemo li samo neko područje na R,pa još neke okolo priče,dotjerali bi do toga da n-ti izvod prolazi kroz sve tačke,u svakoj tački je nula.A to znači da je 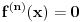 ,n-ti izvod polinoma n-tog stepena. ,n-ti izvod polinoma n-tog stepena.(nešto bi se dalo muljati oko nekih ograđivanja,preciziranja,te šta ako u onom prvom koraku više funkcija ima nultačku baš tu,te ovo te ono i druge stvari.Ja to ne želim niti znam raditi.) [ Nedeljko @ 11.06.2013. 09:26 ] @
[ Nedeljko @ 11.06.2013. 12:03 ] @
Da se razumemo, obzirom da iz uslova sledi da je funkcija polinom (što treba dokazati), izvod nekog reda koji je konstantno jednak nuli postoji, pa samim tim i taj proizvod. Međutim, to treba dokazati.
[ zzzz @ 13.06.2013. 15:20 ] @
Citat: Zahtev zadatka je da za svako  postoji po neko postoji po neko  , za koje je , za koje je 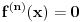 i nigde ne piše da postoji neko i nigde ne piše da postoji neko  takvo da je uvek takvo da je uvek 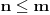 . . Uvedimo baš taj,po volji velik prirodan broj  koji je jednak najvećem koji je jednak najvećem 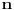 .Nužan i dovoljan uslov da je .Nužan i dovoljan uslov da je  polinom polinom  -tog reda je ako vrijedi -tog reda je ako vrijedi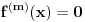 za svako za svako 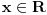 Bojane, izgleda da ja ne mogu da mu objasnim, pa pomozi. 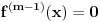 -ti izvod i svi ostali prije njega nisu u potpunosti pokrili -ti izvod i svi ostali prije njega nisu u potpunosti pokrili  skup,ali je to sledeći izvod napravio. skup,ali je to sledeći izvod napravio.Nije lijepo da je prazan,mada neki prethodni mogu biti. Ajmo sada na početak,sa skupovima nula prvog i drugog izvoda.Neka prvi pokriva djelić od  ,a drugi izvod malo poveća taj prostor novim nulama.Uvedimo ovakvu funkciju ,a drugi izvod malo poveća taj prostor novim nulama.Uvedimo ovakvu funkciju 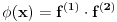 na tom prostoru i zaključimo da će ova funkcija imati vrijednost nula na njemu. na tom prostoru i zaključimo da će ova funkcija imati vrijednost nula na njemu.Prvi izvod takve funkcije takođe je nula.Iz tog izvoda 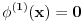 se vidi i da je drugi izvod se vidi i da je drugi izvod 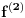 nula na cijelom tom prostoru.Nule prvog izvoda su komplet sadržane u nulama drugog izvoda pa ga odbacimo. nula na cijelom tom prostoru.Nule prvog izvoda su komplet sadržane u nulama drugog izvoda pa ga odbacimo. Prema tački 6 pravilnikaneću tjerati do kraja.Predlažem da to neko kritički i preciznije objasni ili odbaci. [ Nedeljko @ 13.06.2013. 17:19 ] @
Citat: Samo još dokaži da postoji najveći  . Onda je trivijalno. Samo taj detalj fali. Dokaži da nije iskorišćeno beskonačno mnogo prirodnih brojeva . Onda je trivijalno. Samo taj detalj fali. Dokaži da nije iskorišćeno beskonačno mnogo prirodnih brojeva  . .Citat: zzzz: Bojane, izgleda da ja ne mogu da mu objasnim, pa pomozi. Bojane, uključuj se! [ Bojan Basic @ 13.06.2013. 20:55 ] @
@zzzz:
Nedeljko je u pravu. Da probam i ja objasniti u čemu je problem s tvojom idejom. Zamisli da je zadata funkcija  takva da važi takva da važi 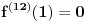 (gde ovo ne važi za izvode reda manjeg od (gde ovo ne važi za izvode reda manjeg od 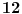 ), zatim ), zatim 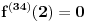 (gde je (gde je 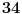 najmanji red), zatim najmanji red), zatim 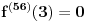 , pa , pa 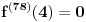 itd. Poenta je, dakle, da bi se možda moglo desiti da ne postoji to tvoje najveće itd. Poenta je, dakle, da bi se možda moglo desiti da ne postoji to tvoje najveće  koje planiraš da uzmeš; koliko god da uzmeš velik prirodan broj koje planiraš da uzmeš; koliko god da uzmeš velik prirodan broj  , da ti u nekoj tački zapravo ipak treba izvod većeg reda od toga što si uzeo. , da ti u nekoj tački zapravo ipak treba izvod većeg reda od toga što si uzeo.[ Nedeljko @ 19.01.2017. 12:16 ] @
Evo malo kraćeg rešenja.
Neka je 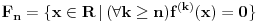 Očigledno je za svako  skup skup 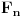 zatvoren. Takođe, zatvoren. Takođe, 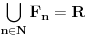 . Iz Berove teoreme o kategorijama sledi da za svaki neprazan otvoren interval . Iz Berove teoreme o kategorijama sledi da za svaki neprazan otvoren interval  postoje postoje  i neprazan interval i neprazan interval 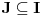 takvi da je takvi da je 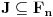 . Pošto je . Pošto je 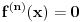 za sve za sve 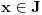 , funkcija , funkcija  je polinom stepena ne većeg od je polinom stepena ne većeg od  na skupu na skupu  . .Neka su 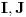 ma koji neprazni otvoreni intervali takvi da je ma koji neprazni otvoreni intervali takvi da je 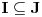 i neka su i neka su 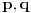 ma koji polinomi i neka je ma koji polinomi i neka je 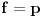 na skupu na skupu  i i 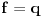 na skupu na skupu  . U tom slučaju, polinomi . U tom slučaju, polinomi  i i  se poklapaju na intervalu se poklapaju na intervalu  , odnosno na beskonačnom skupu tačaka. Polinomi koji su jednaki u beskonačno mnogo tačaka se poklapaju, pa važi , odnosno na beskonačnom skupu tačaka. Polinomi koji su jednaki u beskonačno mnogo tačaka se poklapaju, pa važi 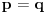 . .Neka je  ma koji interval na kome je funkcija ma koji interval na kome je funkcija  polinomijalna i neka je polinomijalna i neka je  polinom takav da je polinom takav da je 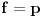 na na  . Na ma kom intervalu . Na ma kom intervalu  na kome je funkcija na kome je funkcija  polinomijalna važi polinomijalna važi 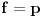 , pa je , pa je 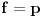 na uniji svih intervala koji sadrže interval na uniji svih intervala koji sadrže interval  i na kojima je funkcija polinomijalna. Stoga je svaki otvoren interval na kome je funkcija i na kojima je funkcija polinomijalna. Stoga je svaki otvoren interval na kome je funkcija  polinomijalna sadržan u nekom maksimalnom otvorenom intervalu na kome je funkcija polinomijalna. polinomijalna sadržan u nekom maksimalnom otvorenom intervalu na kome je funkcija polinomijalna.Različiti maksimalni intervali na kojima je funkcija polinomijalna ne mogu se preklapati jer bi presek ta dva intervala bio interval na kome je funkcija  polinomijalna, pa bi bila jednaka istom polinomu na oba ta maksimalna intervala, kao i na njihovom preseku, odnosno bila bi polinomijalna na uniji ta dva maskimalna intervala suprotno njihovoj maksimalnosti. polinomijalna, pa bi bila jednaka istom polinomu na oba ta maksimalna intervala, kao i na njihovom preseku, odnosno bila bi polinomijalna na uniji ta dva maskimalna intervala suprotno njihovoj maksimalnosti.Neka je  komplement unije svih maksimalnih otvorenih intervala na kojima je funkcija komplement unije svih maksimalnih otvorenih intervala na kojima je funkcija  polinomijalna. Očigledno je zatvoren. polinomijalna. Očigledno je zatvoren.Skup  nema izolovanih tačaka. U suprotnom, postojalo bi neko nema izolovanih tačaka. U suprotnom, postojalo bi neko 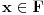 takvo da je takvo da je  polinomijalna u bar nekoj levo poluokolini od polinomijalna u bar nekoj levo poluokolini od 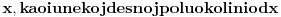 . Postojalo bi neko . Postojalo bi neko  takvo da je takvo da je 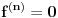 na nekoj okolini od na nekoj okolini od  suprotno uslovu maksimalnosti intervala sa svake strane od suprotno uslovu maksimalnosti intervala sa svake strane od  . .Ako je skup  neprazan, on kao neprazan zatvoren podskup kompletnog metričkog prostora čini kompletan metrički prostor. Obzirom da je neprazan, on kao neprazan zatvoren podskup kompletnog metričkog prostora čini kompletan metrički prostor. Obzirom da je 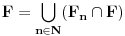 , i da su skupovi , i da su skupovi 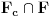 zatvoreni u zatvoreni u  , postoji interval , postoji interval  i i  takvi da je takvi da je 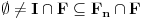 . Dakle, . Dakle, 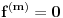 na na 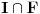 za sve za sve 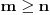 . .Neka je  maksimalan otvoreni podinterval od maksimalan otvoreni podinterval od 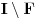 . Na njemu je funkcija . Na njemu je funkcija  jednaka polinomu nekog stepena jednaka polinomu nekog stepena  . Ukoliko to nije nula polinom, važi da je . Ukoliko to nije nula polinom, važi da je 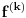 konstanta različita od nule na intervalu konstanta različita od nule na intervalu  . No, zbog neprekidnosti i jednakosti . No, zbog neprekidnosti i jednakosti 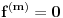 za sve za sve 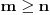 u bar jednoj od krajnjih tačaka intervala u bar jednoj od krajnjih tačaka intervala  (jer barem jedna pripada skupu (jer barem jedna pripada skupu  ), važi ), važi 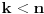 . Dakle, na svakom od takvih intervala je . Dakle, na svakom od takvih intervala je 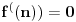 , pa pošto to važi i na skupu , pa pošto to važi i na skupu  , važi i na uniji, odnosno na celom intervalu , važi i na uniji, odnosno na celom intervalu  , odakle je funkcije , odakle je funkcije  polinomijalna na polinomijalna na  , što je u suprotnosti sa , što je u suprotnosti sa 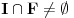 . .Dakle, 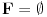 , pa je funkcija , pa je funkcija  polinomijalna. polinomijalna.Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|