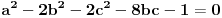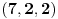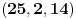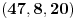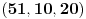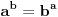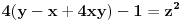[ number42 @ 10.06.2013. 06:54 ] @
|
[ Nedeljko @ 10.06.2013. 10:14 ] @
[ number42 @ 10.06.2013. 17:22 ] @
[ Bojan Basic @ 10.06.2013. 17:41 ] @
[ number42 @ 10.06.2013. 18:13 ] @
Citat: Bojan Basic: Ne mogu odlicno, mislio sam da sam nesto zeznuo a sve to zajedno Citat: jednacina 4(y-x+4xy)-1=z^2 gde su x, y, i z pozitivni celi je nemoguca jer... "leva strana daje ostatak 3 pri deljenju sa 4, a 3 nije kvadratni ostatak po modulu 4." je inace dokaz da u pitagorinoj teoremi a i b ne mogu istovremeno biti neparni. a to sam ustvari hteo da pitam p.s. jel ima neka skracenica na tastaturi za ovaj tex kod, odvalih se svaki put da skrolam da bih nesto stavio pod latex. npr, mishem se obelezi jednacina, i onda klikne skracenica na tastaturi, dal je moguce? mislim da je tako brze 200 puta. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|