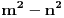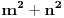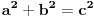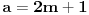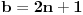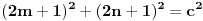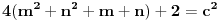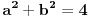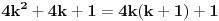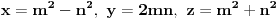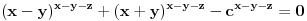|
|
[ number42 @ 11.06.2013. 20:22 ] @
|
| hteo sam da nadjem na netu dokaz o nemogucnosti neparnosti a i b kada su a, b, i c celi pozitivni u pitagorinoj teoremi, ali sam nasao samo za specijalan slucaj pitagorinih trojki sa nekog pmf-a:
pitagorine trojke
i tu se ukratko izvodi dokaz.
ali ne mogu da nadjem za opsti slucaj pitagorine teoreme, a i nije mi jasno ako postoji opsti dokaz, i to jednostavan i opstepoznat- zasto ga izvode u specijalnom slucaju?
ja sam izveo dokaz u nekih 5 redova mozda, pa razmisljam da li sam nesto pogresno sracunao, ili je taj dokaz jako prost pa se i ne pominje.
ali onda- zasto bi izvodili dokaz za specijalan slucaj pitagorinih trojki, nzm, nema logike...
mislim, ovaj dokaz koji sam ja izveo je bas, bas jako prost. svodi se na to da se dva cela pozitivna broja uvek mogu napisati u obliku (x-y) i (x+y) ako su oba istog predznaka, ili (x-y-1) i (x+y) ako su razlicitih predznaka.
i sada ako ih oznacimo kao a i c iz pitagorine teoreme, i kvadriramo pojedinacno pa oduzmemo da bi dobili 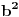 , dobijamo nakon malo racunanja da je , dobijamo nakon malo racunanja da je 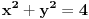 , a to je nemoguce za cele pozitivne brojeve. moze i malo komplikovanije, ali to je to uglavnom, a i b ne mogu biti neparni istovremeno. , a to je nemoguce za cele pozitivne brojeve. moze i malo komplikovanije, ali to je to uglavnom, a i b ne mogu biti neparni istovremeno.
e to me zanima, ne vidim gde gresim, ili neki link za dokaz ako neko zna. |
[ darkosos @ 11.06.2013. 20:34 ] @
A sta ti mislis da je specijalan slucaj Pitagorine teoreme? Na ovom linku sto si dao ne vidim nista specijalno, sve je uradjeno opste...
[ number42 @ 11.06.2013. 21:01 ] @
Citat: A sta ti mislis da je specijalan slucaj Pitagorine teoreme?
pitagorine trojke, npr.
Citat: Na ovom linku sto si dao ne vidim nista specijalno, sve je uradjeno opste...
ne razumem kako je uradjeno opste ako su a i c definisani kao 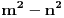 i 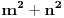 [ darkosos @ 11.06.2013. 21:44 ] @
Uh... To sto si napisao je zakljucak tog dokaza, a teorema koja se dokazuje je opstija od tvog zakljucka o parnosti kateta.
Elem, na jednoj prethodnoj temi ovde ti je Bojan zavrsio taj dokaz iz ove teme, a probaj sad ovako:
u najobicnijoj PT, 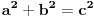 , stavi da je 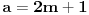 i 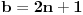 , dakle da su obe katete neparni brojevi. Zamenom u PT se dobija:
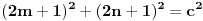 iliti 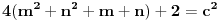 i na to se na potpuno isti nacin moze primeniti logika koju ti je Bojan izneo. Dakle bez koriscenja tvog "opsteg" oblika PT. [ number42 @ 11.06.2013. 23:17 ] @
@darkosos,
zanimljivo zaista. nije mi palo na pamet da a i b izrazim kao u gornjem primeru, jer sam verovao da tako ne mogu nista dobiti.
da, bojan je dovrsio dokaz ove slozenije varijante, a za koju zaista ne znam kako je to izveo sa deljivoscu i moduo i slicno, al valjda naucim jednom 
al evo dao sam neki prostiji dokaz u prvom postu, gde dolazis do kontradikcije koju svako moze da uoci 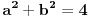 .
pretpostavljam onda da se neparnost a i b uzima zdravo za gotovo, i da se ne raspravlja mnogo o tome, zato me i zacudilo da se to objasnjava kod pitagorinih trojki (i to na faxu).
a kako se objasnjava ako se uzima zdravo za gotovo? a i onda bi bilo negde na netu, zar ne...
nzm...
konkretno za tvoj primer, covek treba da zna da 4x+2 ne moze biti kvadrat. a valjda i to nekad mora da se nauci, sta i kako, itd.
opet se vracemo na cinjenicu da mora postojati dokaz, tj sled izvodjenja, a ja nisam video prostiji od ove krajnje kontradikcije 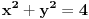 , koje se prosto intuitivno moze znati u osnovnoj skoli. [ electropioneer @ 12.06.2013. 05:36 ] @
Citat: konkretno za tvoj primer, covek treba da zna da 4x+2 ne moze biti kvadrat. a valjda i to nekad mora da se nauci, sta i kako, itd.
4x+2 = 2(2x+1)
2x+1 nije deljivo sa 2 [ darkosos @ 12.06.2013. 07:37 ] @
@electropioneer
Lepo si to primetio, znaci sada je jos prostije :)
@number42
Prikazi svoj dokaz, bas me zanima koliko je tacno prostiji od ovoga?
[ number42 @ 12.06.2013. 15:51 ] @
Citat: @number42
Prikazi svoj dokaz
pa u prvom je postu. [ darkosos @ 12.06.2013. 18:11 ] @
Nisi pokazao ceo racun, pa sam zato hteo da vidim koji je prostiji...
Pa, da zakljucimo onda ovako: na linku koji si dao postoji dokaz koji ide otprilike ovako: kvadriranjem 2k+1 se dobija izraz 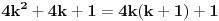 koji kada se deli sa 8 daje ostatak 1 - jer je k(k+1) uvek paran broj; sabiranjem dva ovakva broja se dobija paran broj koji posle deljenja sa 8 daje ostatak 2, pa ne bi bio deljiv sa 4, sto bi moralo biti.
Ovo je slicno onome kako sam ja uradio, i meni se cini prilicno jednostavnim. E sad da li je "bas bas prilicno prost" ne znam :)
Citat: e to me zanima, ne vidim gde gresim, ili neki link za dokaz ako neko zna.
Dakle, nigde ne gresis, osim u proceni da si dobio nesto bas bas mnogo prostije, i u tome da tvoj "opsti oblik" Pitagorine teoreme sluzi necemu posebnom.
A opste predstavljanje Pitagorinih trojki 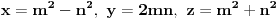 si vec dobio u temi http://www.elitesecurity.org/t463873-0#3276257, i ono je bolje jer daje primitivne Pitagorine trojke, dakle one koje nemaju zajednickih faktora, pa predstavljaju generatore svih ostalih. [ number42 @ 12.06.2013. 22:04 ] @
da,da, kontam, moj nacin je jednostavniji 
pusti to, zanima me druga stvar. u pokusaju da uprostim dokazivanje makar dela fermata, zamenio sam a=x-y b=x+y n=x-y-z, a c ostavio kao c.
e sad, tu postoji vise varijanti ako pokusamo da ih na ovaj nacin zamenimo sa 3 promenljive, nekih 12 ako sam dobro izracunao (s obzirom na parnost, sta je vece, i sl), ali sam hteo da vidim da li princip uspeva, pa sam odabrao jednu.
nisam siguran da li se ovim vrtim u krug, ali osnovna ideja je da dobijem razlomak koji ce biti jednak nuli, onda je ono iznad jednako nuli, to se malo sredi i mozda dobije nemogucnost jednakosti. to je taj lukavi plan 
imamo ovako nesto
(samo pojasnjenje, uslov je x>4 (da se ne bi svodilo na pitagorinu teoremu, tj n=2 kad su y i z jedinice)
x, y, z, i c, su pozitivni celi brojevi i x>4. za svako x, y, i z, postoji neko c za koje je sledeca jednakost tacna:
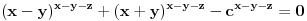
uglavnom, treba neko ovo caskom da mi izracuna 
.
[ darkosos @ 13.06.2013. 08:03 ] @
Ne ne decko, grdno gresis, moj nacin je jednostavniji :)
Elem, racunaj bre sam, vezbaj... Ti bi da smisljas ideje, a mi da ti racunamo? Stvarno mislis da ces takvim pristupom otkriti nesto? Nemoj pogresno da me razmes, sve je to lepo sto tebe to zanima i tako dalje, ali tvoje pretenzije su u neravnotezi sa znanjem i spremnoscu da ulozis odgovarajuci napor da isteras makar i to sto si zamislio... Pritom je to sve vec toliko puta prezvakano da nema druge svrhe, osim da ti sam naucis nesto o temama koje te zanimaju.
[ Nedeljko @ 13.06.2013. 15:18 ] @
Za ostale clanove (bez clana number42)
Na PP mi je rekao da sam opsednut formom i dogovorili smo se da ne odgovaramo jedan drugome. Darko, tvoj način jeste korektan, ali postoji još "lakši" - pomnožiš nulom, pa onda skratiš. Mislim da bi njemu takva rešenja daleko više odgovarala. Džabe se trudite ovako. Ispašćete formalisti kao ja.
[ number42 @ 13.06.2013. 15:31 ] @
@darkosos,
znas kako, cini mi se da je resavanje hipoteza i teorema prilicno zanimljiv nacin za ucenje stvari koje su nezanimljive, nerazumljive ili nepoznate. ako uz to jos i nesto i dokazes- eto bonus, jer svako od tih dokazivanja je izazov sam po sebi.
a nisam bas siguran u tvoj stav da postoji cvrsta korelacija izmedju ideja i kolicine znanja, cak verujem da u nekom trenutku solidna obrazovanost moze da predstavlja kocnicu za ideje, jer je stecena na nacin koji ostavlja utabane staze razmisljanja, a to je automatski manjak kombinacija u razmisljanju, to je onda manjak kreativnosti, i onda to povlaci manjak ideja.
ma koliko ovo tesko padalo ljudima koji su ceo zivot posvetili nekoj stvari, cini mi se da ima prilicno primera koji ovo pokazuju, jednostavno treba da se pomire s tim.
a i plus, neko moze iz tri informacije da izvuce 50 ideja, a neko iz 50 informacija tri ideje...
nzm, moje misljenje je da je idealna kombinacija sinergija razmisljanja ljudi koji sa razlicitih aspekata sagledavaju jednu istu stvar, na razlicitim nivoima generisanja ideja.
a konkretno za formulu u proslom postu- ono, nije 'must to', vec ako neko zeli da vidi da li ideja prolazi ok, ako ne nista, videcu wolfram alpfha sta kaze 
[ darkosos @ 13.06.2013. 16:10 ] @
Jasno, svi veliki matematicari su zapravo bili matematicki polupismeni... Ovo je sve sada vec van teme.
[ number42 @ 13.06.2013. 16:26 ] @
e sad ne znam odkud to da su svi veliki matematicari bili polupismeni?!
koliko mi je poznato vecina je saradjivala na razradi svojih dostignuca, mozda je izuzetak grigorij perelman pre nego se povukao.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|
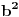 , dobijamo nakon malo racunanja da je
, dobijamo nakon malo racunanja da je 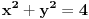 , a to je nemoguce za cele pozitivne brojeve. moze i malo komplikovanije, ali to je to uglavnom, a i b ne mogu biti neparni istovremeno.
, a to je nemoguce za cele pozitivne brojeve. moze i malo komplikovanije, ali to je to uglavnom, a i b ne mogu biti neparni istovremeno.