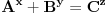[ number42 @ 11.06.2013. 21:08 ] @
| da li je ovim mozda oborena fermatova teorema? Bosanac rešio zadatak vredan milion dolara? malo sam surfao i ako dobro razumem, ovaj covek koji nudi nagradu je izneo tvrdnju da je tacno 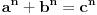 ako su a,b, i c uzajamno prosti brojevi, a to valjda znaci da, kako su a, b, i c proizvodi nekih brojeva- onda nijedan broj ne sme biti isti kao neki drugi. ako su a,b, i c uzajamno prosti brojevi, a to valjda znaci da, kako su a, b, i c proizvodi nekih brojeva- onda nijedan broj ne sme biti isti kao neki drugi.ispravite me ako gresim, jer nisam siguran ovde ni sta je pitanje ni da li je ovo obaranje fermata (iako postoji dokaz?!). [Ovu poruku je menjao number42 dana 12.06.2013. u 17:11 GMT+1] |