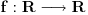[ Nedeljko @ 12.06.2013. 10:49 ] @
|
[ darkosos @ 12.06.2013. 20:59 ] @
Nemam bas neki dokaz, ali evo nekog razmisljanja:
Ako funkcija ima lokalni minimum u nekoj tacki, onda postoji okolina te tacke u kojoj su sve vrednosti funkcije vece ili jednake od vrednosti u toj tacki. Po uslovu zadatka, svaka tacka je lokalni minimum; proizvoljna okolina tacke je skup koji sadrzi otvoren skup, pa je neprebrojiv u R; za svaku tacku iz tog skupa vazi da su vrednosti funkcije ostalih tacaka vece ili jednake; ako je ovakva funkcija na nekom intervalu neprekidna, onda je ona tu i konstatna; ako funkcija u nekoj tacki a ima prekid, onda tu ima vrednost manju nego u intervalima (a-e, a) i (a, a+e) za neko e. Ovo poslednje se moze opravdati time da funkcija moze imati samo prebrojivo mnogo prekida (iskop'o sam to negde iz malog mozga). Jasno je da ne mozemo da nanizemo samo disjunktne otvorene intervale da bi dobili ceo R. Ako je funkcija neprekidna na R, onda je konstantna, pa je tvrdjenje tacno. Ako je X skup prekida (najvise prebrojiv), onda skup vrednosti fukcije sadrzi sve razlicite vrednosti iz skupova X i unije otvorenih intervala na kojima je fukcija neprekidna, sto jeste najvise prebrojivo. Funkcija bi mogla da izgleda ovako: na recimo intervalima (k, k+1) za cele brojeve k ima vrednost k, a u tackama x=k ima vrednost k-2, da bi bila manja od vrednosti u susednim intervalima (k-1,k), (k,k+1). [ Nedeljko @ 12.06.2013. 22:54 ] @
Citat: darkosos: funkcija moze imati samo prebrojivo mnogo prekida Ovo nije tačno. Funkcija koja je u svim racionalnim tačkama jednaka jedinici, a u svim iracionalnim jednaka nuli ima prekid u svakoj tački. To tvrđenje je tačno za na primer funkcije koje su na svakom ograničenom intervalu ograničene varijacije. Citat: darkosos: Funkcija bi mogla da izgleda ovako: na recimo intervalima (k, k+1) za cele brojeve k ima vrednost k, a u tackama x=k ima vrednost k-2, da bi bila manja od vrednosti u susednim intervalima (k-1,k), (k,k+1). Ovo je dobro. [ darkosos @ 13.06.2013. 06:03 ] @
Onda ne znam :) Na okolini tacke u kojoj je ona lokalni minimum funkcija mora biti konstantna. Dakle fali da se pokaze da R ne moze sadrzati uniju neprebrojivo mnogo disjunktnih otvorenih intervala.
[ darkosos @ 13.06.2013. 07:57 ] @
U stvari, kad covek bolje razmisli, a ne ovako kao ja, svaki otvoreni interval (neprazan) sadrzi bar jednu tacku iz Q, pa posto su disjunktni, ovi brojevi su razliciti, pa ih ima najvise prebrojivo mnogo. Da li je ovo sad ok?
[ Nedeljko @ 13.06.2013. 10:44 ] @
[ darkosos @ 16.06.2013. 19:39 ] @
Ne, nije, naravno... Nego nisam nesto stizao da kvalitetnije odgovorim. A mozda to necu uciniti ni sada :)
U svakom slucaju, ono sto se moze lako primetiti za ovakvu funkciju je sledeca osobina: ako je 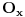 okolina tacke x u kojoj je ona lokalni minimum i ako postoji okolina tacke x u kojoj je ona lokalni minimum i ako postoji 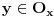 takvo da je takvo da je 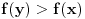 , tada postoji okolina , tada postoji okolina 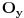 tacke y, takva da je tacke y, takva da je 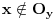 . Ovo je naravno zato sto mora postojati okolina tacke y u kojoj je ona lokalni minimum, pa takva ne moze sadrzati x, jer je vrednost funkcije u y veca. . Ovo je naravno zato sto mora postojati okolina tacke y u kojoj je ona lokalni minimum, pa takva ne moze sadrzati x, jer je vrednost funkcije u y veca.E sad, kako ovo iskoristiti? Evo nekog pokusaja: navedena logika se dalje moze nastaviti na okolinu tacke y, itd. Time dobijamo jedan niz okolina, neka su to recimo otvoreni intervali, koji ne bi smeo da ima prazan presek. Cini mi se da u tom slucaju, tacka koja bi se dobila kao granicna vrednost niza tacaka sa navedenom osobinom, ne bi imala okolinu u kojoj je lokalni minimum funkcije f. Ako je tako, onda znaci da smo dobili, kao presek u navedenom postupku, otvoreni interval u kome nema tacaka u kojima funkcija ima strogo vecu vrednost od tacke lokalnog minimuma, pa je znaci tu konstantna. Dalje bi se mogla koristiti ranije navedena logika... [ Nedeljko @ 16.06.2013. 20:30 ] @
Time si dokazao da svaka okolina ima podokolinu u kojoj je funkcija konstantna. Pazi, tu osobinu ima i Kantorova lestvica, koja je surjektivno neprekidno preslikavanje [0,1] na [0,1]. Dakle, odatle još uvek ne sledi da je skup vrednosti funkcije najviše prebrojiv.
[ Nedeljko @ 17.06.2013. 10:16 ] @
Treba li pomoć?
[ darkosos @ 17.06.2013. 10:51 ] @
Probacu jos malo da se mucim... Znam da sam spor, ali sam zato uporan :) Nadam se da cu stici ovih dana da shvatim da li treba da se predam :) A ako ti je dojadilo, ti postavi resenje. Ili se mozda pojavi neko treci pa resi.
[ Nedeljko @ 17.06.2013. 18:15 ] @
Pazi, možeš ti da rešiš problem i na alternativan način - razbijanjem AES 256 ključa rešenja priloženog uz prvu poruku. Odmah da ti kažem da lozinka uključuje mala i velika slova engleske abecede, cifre i ostale ASCII znake, da je duža od 10 znakova i da su znaci nasumično odabrani. Ako uspeš, priznaje se.
Međutim, postoji daleko jednostavnije rešenje. [ darkosos @ 17.06.2013. 20:45 ] @
Ma verujem da ima, ja sam do onog primera dosao tako sto sam pokusavao da zamislim funkciju, pa sam prvo skapirao da mora da ima te intervale konstantnosti, a onda jos malo to dobrusio da bih dobio celu funkciju. Ne vidim da bih istom logikom mogao da i dokazem tvrdjenje, jer sam koristio, da tako kazem, konstruktivisticki pristup - prvo sam video da intervali konstantnosti moraju biti otvoreni, a onda jos smislio sta sa "rupama". S' druge strane, mogao bih da pretpostavim suprotnom pa trazim kontradikciju, ali vise volim da pratim intuiciju...
Sto se tice razbijanja kljuca, pa nisam u tom fazonu. Kad bi mi to bi gust, onda bih zeleo i da razbijem sifru i da resim zadatak. Ovako mi je samo gust da ga resim, ali se ne opterecujem vremenom. Evo sa'cu da sednem da porazmislim malo, obecavam :) [ Nedeljko @ 17.06.2013. 21:16 ] @
Prethodna poruka je naravno bila šala.
[ Nedeljko @ 25.06.2013. 16:53 ] @
Dakle, jesi li s predao ili hoćeš hint?
[ darkosos @ 25.06.2013. 20:17 ] @
E, pa ne znam, nikako da nadjem dovoljno vremena da se ozbiljnije pozabavim, a prilicno sam izgleda "zahrdjao" :) I izgleda se u medjuvremenu posvadjao sa cika Kantorom :) Mozda imam previse konstruktivisticki pristup, pokusavam da zamislim, ali nesto ne ide. Mislim da sam napravio primer i gde funkcija u (0,1) ima prebrojivo mnogo vrednosti. To mozda i ne cudi jer su u tom smislu (0,1) i R isto...
Tako da, eto, moze hint, mada ne znam sta bi to bilo? Da li je ono sto sam pokazao za podokoline neki polaz? [ Nedeljko @ 25.06.2013. 21:29 ] @
Q je prebrojiv svuda gust podskup of R.
[ ivan90BG @ 26.06.2013. 08:09 ] @
Pozdrav, mislim da imam dobru ideju.
To je funkcija koja se sastoji od konačno ili beskonačno mnogo spojenih konstantnih funkcija različitih vrednosti, ali spojenih na takav način da je u tačkama spajanja interval one konsatnte koja je manja od susedne zatvoren u toj tački, a interval susedne u toj tački otvoren. Ovo bi trebalo da osigura da funkcija u svim tačkama spajanja ima lokalni minimum, jer pošto je interval sa druge strane tačke spajanja (gde je vrednost funkcije veća) otvoren, ako se uzme bilo koja tačka iz intervala veće konstante koja je proizvoljno blizu tačke spajanja uvek će postojati neka okolina u kojoj je funkcija konstantna i jednaka vrednosti u izabranoj tački. Naravni ako se izabere sama tačka spajanja, ona je minimum zbog načina spajanja. I tako je svaka tačka funkcije nestrogi lokalni minimum, a takođe je skup njenih vrednosti prebrojiv (iako možda beskonačan): to je niz konstanti kojih moože biti beskonačno mnogo i u pozitivnom i u negativnom smeru funkcije. Vrednosti se mogu nabrojavati presecanjem niza vrednosti na dva dela (koja će sada sigurno biti zatvorena na jednoj strani) i brojanjem naizmenično vrednosti iz jednog pa iz drugog niza. Jel vredi ovo nešto? [ darkosos @ 26.06.2013. 12:03 ] @
Ako sam dobro shvatio, to su intervali tipa
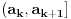 koji se nastavljaju jedan na drugi i u kojima je funkcija konstantana. I u prethodnom f uzima vrednost manju nego u narednom, da bi u okolini tacke koji se nastavljaju jedan na drugi i u kojima je funkcija konstantana. I u prethodnom f uzima vrednost manju nego u narednom, da bi u okolini tacke 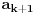 koja mora da sece naredni interval, funkcija imala lokalni minumum. Mislim da je korektno kao primer, ali ne i kao dokaz. Posebno sto ne mora da bude tako, pogledaj moj primer sa pocetka. koja mora da sece naredni interval, funkcija imala lokalni minumum. Mislim da je korektno kao primer, ali ne i kao dokaz. Posebno sto ne mora da bude tako, pogledaj moj primer sa pocetka.@Nedeljko Nesto mi to ne pomaze :) Formalno, kada bih nasao preslikavanje 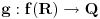 koje je 1-1, dokazao bih da je f(R) najvise prebrojiv, ali nemam pojma kako bih to i zapoceo. S' druge strane, taj argument, da je Q to sto si napisao u hintu, sam vec koristio u nekom od propalih pokusaja. Dakle, drugi pristup, meni blizi, je da pokazem da tacaka u kojima funkcija ima strogi minimum moze imati najvise prebrojivo mnogo. To je to oko cega sam se inace vrteo... koje je 1-1, dokazao bih da je f(R) najvise prebrojiv, ali nemam pojma kako bih to i zapoceo. S' druge strane, taj argument, da je Q to sto si napisao u hintu, sam vec koristio u nekom od propalih pokusaja. Dakle, drugi pristup, meni blizi, je da pokazem da tacaka u kojima funkcija ima strogi minimum moze imati najvise prebrojivo mnogo. To je to oko cega sam se inace vrteo...[ Nedeljko @ 26.06.2013. 13:24 ] @
ivan90BG.
Intervali se ne moraju nastavljati jedan na drugi. Vidi kako izgleda komplement Kantorovog skupa. Između svaka dva maksimalna intervala postoji neki interval. darkosos, Posmatraj Q u domenu, a ne u kodomenu. Poenta sa Q je da ne moraš tražiti neki prebrojiv, a gust podskup od R, koji je odgovarajući za datu funkciju, već da za svaku funkciju koja zadovoljava uslove zadatka možeš da koristiš bilo koji takav podskup, na primer uvek Q. [ Nedeljko @ 27.06.2013. 12:54 ] @
Evo još jedne pomoći:
Posmatrati intervale u domenu sa racionalnim krajevima. [ darkosos @ 28.06.2013. 14:31 ] @
Vidis, uopste nisam imao taj pristup... Da jesam, verovatno bi mi jos prvi hint znacio. Pa pretpostavljam da treba posmatrati intervale koji su okoline koje moraju da postoje zbog uslova zadatka. Ali ne moze svaka tacka sa R da ima ovakvu okolinu samo za sebe, hocu reci disjunktnu sa ostalim. Verovatno se onda mora izvuci zakljucak da postoje intervali koji su trazene okoline za sve tacke tog intervala. Aj' razmislicu jos ako je to taj put...
[ Nedeljko @ 29.06.2013. 07:45 ] @
Evo uzgred lozinke za rešenje:
]iQrdQk&-;:);v92k!m!j Rešenje dostavljam i u prilogu. Ko neće, ne mora da čita. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|