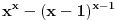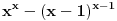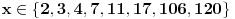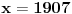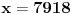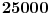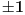[ number42 @ 14.06.2013. 13:50 ] @
|
[ igorpet @ 14.06.2013. 15:12 ] @
Ako podjemo od pretpostavke da ima beskonacno mnogo brojeva, onda i ovaj izraz "generise" beskonacno mnogo brojeva.
Ako se podje od pretpostavke da ima beskonacno mnogo prostih brojeva onda bi trebalo da i ovaj izraz daje kao rezultat besonacno mnogo prostih brojeva (bez obzira na to da li ih mi mozemo ili ne mozemo generisati i izracunati). Ako ovaj izraz daje, osim ovih 6 prostih, samo slozene brojeve onda bi to bilo veliko dostignuce (po meni barem). A ovaj izraz je dobijen ...??? kako [ number42 @ 14.06.2013. 16:28 ] @
Citat: A ovaj izraz je dobijen ...??? kako ma bzv, lupio. zanimaju me prosti brojevi, pa sam hteo da proverim neki izraz koji ce imati nepravilnu raspodelu x kad je izraz prost broj, i onda ako se ta raspodela x-ova poklapa sa raspodelom prostih, onda je to vec neki shablon, jel. a ovo me bas zacudilo, kad sam dosao do 11, pomislio sam da sam eto nekim slucajem naleteo na fibonacijev niz, a to bi vec bilo cudo. ali nakon toga 17, i nista... u prvih 20 brojeva ima 6 koji daju prost izraz, u drugih 20 nijedan. ne znam sta da mislim, da li je to fascinantno ili ne, bilo koji ishod da je moguc, da ih ima beskonacno ili konacno, ili samo 6... trebalo bi da je u korelaciji sa verovatnocom i da se smanjivanjem verovatnoce pojavljivanja prostog broja na tako velikim brojnim rastojanjima takodje smanjuje i samo pojavljivanje prostih kao rezultat izraza. nzm... al to je kada je razlika. a evo proverio sam i za zbir, kada je izraz 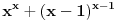 , i izraz je prost samo za 3 broja, 2, 3, i 4 (a dogurao sam do x=31), i ni za jedan broj vise nije prost. , i izraz je prost samo za 3 broja, 2, 3, i 4 (a dogurao sam do x=31), i ni za jedan broj vise nije prost.[ Bojan Basic @ 14.06.2013. 20:26 ] @
[ igorpet @ 14.06.2013. 22:29 ] @
Citat: number42: Citat: A ovaj izraz je dobijen ...??? kako ma bzv, lupio. ... Znaci intuitivna metoda Jel svaki put kad "lupis" neki izraz ti se studiozno bavis njime? Ako je tako izgubices silno vreme ... a rezultata najverovatnije nece biti. Prouci prvo sve ono sto je vec "smisljeno" i objavljeno (barem sada nije neki problem pronaci informacije) pa onda kreni da "smisljas" sam. Nisam bas nesto mnogo kompetentan u vezi teorije brojeva, ali mislim da ces ovim principom stici dalje. Ako te interesuju prosti brojevi mozda za pocetak da pogledas: formuly_dlya_prostyh_chisel Prime Number Diagrams Citat: Let's look at the modulo 40 layout. You'll notice that the primes all fall on several radials, and avoid others. This is easily explained. Every other radial represents an even number, and no even numbers past 2 are prime. Similarly, every fifth radial represent multiples 5, preventing primes along the length of its vector. Two, and Five are the positive, prime, integer factors of our modulo, 40 (the full set of factors is 1, 2, 4, 5, 8, 10, 20, 40). There seems to be no magic to this, and no human-perceivable pattern to the distribution of primes within the prime-permitting radial vectors. However, I've saved the best for last. There is one last, mind-blowing mystery revealed by this chart. Outside of the first, inner ring, ALL of the prime squares (numbers that are a prime number squared) ALL fall into two columns -- the first and ninth. Ako ovo vec nisi znao, mozda ti da neku novu ideju ... [Ovu poruku je menjao igorpet dana 15.06.2013. u 00:24 GMT+1] [ number42 @ 14.06.2013. 23:28 ] @
@igorpet,
pa pretpostavljam da je i intuitivno razmisljanje neki vrst podsvesnog razmisljanja i da je u istoj meri podlozno greskama i ispravnim zakljuchcima. a uglavnom svi mi razmisljamo i svesno i podsvesno i donosimo zakljuchke. a usvajanje znanja na sistematican nacin koji predlazes je samo jedan od nacina ucenja, a mislim da svakome odgovara drugaciji nacin jer ljudi razlicito razmisljaju. staviti ih sve pod jedan kalup, tj da svi uce na isti nacin- meni je to neshvatljivo, ne razumem kako to moze da da optimalne rezultate, da ne govorim o maksimalnim. o ovome je jako dobro pisao toni buzan u svojim knjigama, povezivanje apstraktnog i konkretnog, pamcenje, ucenje, i sl, toplo preporucujem svima. teorija brojeva nije jedina stvar koja me zanima, recimo tu je i geometrija, a koja se naslanja na nju, npr stepenovanje se moze svesti na jako prostu geometriju, ovo se dalje nadovezuje na nesto drugo, itd. @bojan basic, znaci nista... ok. EDIT: @igorpet, hvala na linkovima, ali ne baratam stranim jezicima, samo engleski vrlo prosto (i to sam najbolje ucio iz filmova [ igorpet @ 15.06.2013. 00:30 ] @
@number42
hteo sam samo da ti ukazem da je "smisljanje" izraza za generisanje necega prilicno kompleksna stvar i obicno nije proizvod intuicije vec sistematskog rada. Npr. "rekorder" u generisanju prostih brojeva n^2+n+41 (vazi za n=0 .. 40) da li znas kako je nastao? Nije se slucajno doslo do ovog izraza vec proucavanjem Ulamove spirale, kao i jos neki izrazi ... Vizuelizacija prostih brojeva u mnogome je doprinela u pojedinim oblastima proucavanja. Izlazak iz postojeceg "sablona" rada i razmisljanja moze biti iskorak i dovesti do rezultata ali to je u stvari opet neki novi "sablon" rada i razmisljanja a ne puko nagadjanje. Iskorakom iz postojeceg "sablona" npr. nastala je hiperbolicka geometrija ali je ona samo stvorila nov "sablon" nije nastala tek onako, "lupili" pa pogodili. Proste brojeve su proucavali i jos uvek proucavaju na puno nacina, svaki novi iskorak i novi metod doneo je po nesto novo i interesantno, pa logicno je da za nesto novo trebamo osmisliti i nov metod. Mada ne znaci da se proucavanjem i postojecih ne moze otkriti nesto novo. Ne znam da li sam ti uopste jasan ali metoda probe je u principu najgora i najsporija metoda, i ne znam da li moze dovesti do nekih bitnih rezultata i to je ono glavno sto sam ti hteo reci. I npr. da li si nekad razmisljao da sa sadasnjom snagom racunara mi mozemo izgenerisati sve moguce i nemoguce matematicke izraze (za par stotina ili hiljada godina ili ... vec). Ubacis oznake, simbole, slova ... i zadas da redom pravi sve moguce kombinacije ... bice generisamo na milijarde i milijarde simbola i ako postoji univerzalni izraz za generisanje prostih brojeva on ce sigurno biti medju njima, ali jos niko nije krenuo tim putem jer on (barem za sada) sigurno ne vodi nikuda. Zato se za sada ide putem koji sistematizuje stvari i donosi izraze na osnovu proucavanja nekih metoda a ne obrnuto. Ali i pored navedenog, ljudska svest i razmisljanje su ipak nepredvidivi i prihvatam mogucnost da si ti, mozda, u pravu. [ Bojan Basic @ 15.06.2013. 00:42 ] @
Citat: igorpet: Npr. "rekorder" u generisanju prostih brojeva n^2+n+41 (vazi za n=0 .. 40) da li znas kako je nastao? Mala (možda) ispravka: nisam sasvim siguran u kom si kontekstu upotrebio termin „rekorder“, no mislim da ovaj polinom ipak ne predstavlja rekord ma kakvog tipa (iako jeste zanimljivo da izbacuje proste brojeve za sve vrednosti argumenta od  do do 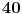 , pa se ova zanimljivost često navodi). Štaviše, postoji polinom čije sve pozitivne vrednosti upravo pokrivaju sve proste brojeve (ništa više, i ništa manje od toga!), a pominjali smo ga i na ES-u: http://www.elitesecurity.org/p2106469. , pa se ova zanimljivost često navodi). Štaviše, postoji polinom čije sve pozitivne vrednosti upravo pokrivaju sve proste brojeve (ništa više, i ništa manje od toga!), a pominjali smo ga i na ES-u: http://www.elitesecurity.org/p2106469.[ Nedeljko @ 15.06.2013. 01:30 ] @
Bojane, ovaj kvadratni polinom je polinom po jednoj nepoznatoj.
[ Bojan Basic @ 15.06.2013. 01:40 ] @
Pošto igorpet nije precizirao na kakvu vrstu rekorda je mislio, ja sam naveo najekstremniji primer koji sam imao pri ruci.
 pa do što veće gornje granice (da li sam sad dovoljno restriktivan? pa do što veće gornje granice (da li sam sad dovoljno restriktivan? 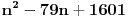 da je proste vrednosti za da je proste vrednosti za  u rasponu od u rasponu od  do do 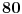 . .[ number42 @ 15.06.2013. 06:47 ] @
Citat: hteo sam samo da ti ukazem da je "smisljanje" izraza za generisanje necega prilicno kompleksna stvar i obicno nije proizvod intuicije vec sistematskog rada. Ali i pored navedenog, ljudska svest i razmisljanje su ipak nepredvidivi i prihvatam mogucnost da si ti, mozda, u pravu. igorpet, nemam pojma, znam samo da sam primetio kada nesto lupim to cesto bude mnogo pametnije nego kada smisljam danima. to je cist dokaz :P [ igorpet @ 15.06.2013. 14:55 ] @
Citat: Bojan Basic: Pošto igorpet nije precizirao na kakvu vrstu rekorda je mislio, ja sam naveo najekstremniji primer koji sam imao pri ruci.  pa do što veće gornje granice (da li sam sad dovoljno restriktivan? pa do što veće gornje granice (da li sam sad dovoljno restriktivan? 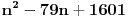 da je proste vrednosti za da je proste vrednosti za  u rasponu od u rasponu od  do do 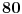 . .Da, mislio sam na to sto si naveo ali nisam znao za 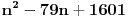 Ali i ovaj polinom, verovatno, nije nastao slucajno vec je rezultat rada i proucavanja ... Citat: number42: nemam pojma, znam samo da sam primetio kada nesto lupim to cesto bude mnogo pametnije nego kada smisljam danima. to je cist dokaz :P [ number42 @ 15.06.2013. 17:34 ] @
@igorpet,
pa mislim da da, razlicitim senzibilitetima odgovara razlit nacin usvajanja znanja, razradjivanja, donosenja zakljucaka i sl. nego, hteo sam nesto da pitam da li neko zna: da li program na racunaru moze da generise funkciju kao grafik i nakon toga, na osnovu grafika, da generise i obelezi tacke grafika cije su koordinate (x,y) celi brojevi? ideja je sledeca: ako imamo funkciju 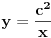 gde je c neki ceo pozitivan broj a x i y promenjive koje se krecu u okviru celih pozitivnih brojeva (dakle ceo grafik je smesten u gornjem desnom kvadrantu), onda (ako program moze iz grafika da generise ove tacke) mozemo da zakljucimo da li je c prost broj ili ne. gde je c neki ceo pozitivan broj a x i y promenjive koje se krecu u okviru celih pozitivnih brojeva (dakle ceo grafik je smesten u gornjem desnom kvadrantu), onda (ako program moze iz grafika da generise ove tacke) mozemo da zakljucimo da li je c prost broj ili ne.u slucaju da je slozen, racunar ce generisati neki neparan broj takvih tacaka, a u slucaju da je c prost broj- racunar ce generisati samo jednu tacku na grafiku, a cije koordinate su x i y jednaki celi pozitivni brojevi. ovo prosto proizilazi iz (geometrijske) cinjenice da se bilo koji kvadrat cije su stranice prosti brojevi nikada ne moze transformisati u pravougaonik cije su stranice celi brojevi, a kvadrat cije su stranice slozeni brojevi se uvek moze transformisati u pravougaonik cije su stranice celi brojevi. dakle, stvarno nemam pojma da li je ovo moguce graficki odraditi. znam da je brojcano jako tesko za velike brojeve i da su potrebni superracunari, ali ne znam kako stvari stoje kada imamo koordinatni sistem i na njemu grafik neke funkcije... da ponovim pitanje: da li program na racunaru moze da generise funkciju kao grafik i nakon toga, na osnovu grafika, da generise i obelezi tacke grafika cije su koordinate (x,y) celi brojevi? (nema potrebe da program zna ili izracuna koja je vrednost tih brojeva x i y, samo da li su celi ili ne) [ igorpet @ 15.06.2013. 17:57 ] @
Citat: number42: ... da ponovim pitanje: da li program na racunaru moze da generise funkciju kao grafik i nakon toga, na osnovu grafika, da generise i obelezi tacke grafika cije su koordinate (x,y) celi brojevi? (nema potrebe da program zna ili izracuna koja je vrednost tih brojeva x i y, samo da li su celi ili ne) Ako sam dobro razumeo, ovaj problem se resava jako jednostavno programski za datu funkciju (ako sam dobro shvatio c je konstanta.): - za x dodeljujes celobrojne vrednosti - izracunas koliko je y - proveris da li je y ceo broj ili nije - ako jeste ucrtas tacku na grafikonu - ides ponovo sa novom celobrojnom vrednoscu za x ... Tako ce na grafikonu da ti budu ucrtane samo koordinate koje su celobrojne vrednosti. Ako zelis, mozes prvo na grafikonu iscrtati funkciju klasicno a zatim dodati tacke gde su vrednosti celobrojne. A mozes i drugacije, prvo nadjes delioce broja c^2 i jedino kada je vrednost za x jednaka deliocu izraz ce biti celobrojan. (Divisors and Factorization) [ number42 @ 15.06.2013. 18:09 ] @
da, to je numericko resavanje.
kod njega je problem sto je za ogromne vrednosti c, npr za broj koji ima 10 milijardi cifara, prilicno tesko naci delioce. zato sam i pitao da li postoji mogucnost ovakvog grafickog resavanja, da bi se zaobisli numericki metod i neophodnost tacnog izracunavanja delilaca. [ igorpet @ 15.06.2013. 18:21 ] @
Citat: number42: da, to je numericko resavanje. kod njega je problem sto je za ogromne vrednosti c, npr za broj koji ima 10 milijardi cifara, prilicno tesko naci delioce. zato sam i pitao da li postoji mogucnost ovakvog grafickog resavanja, da bi se zaobisli numericki metod i neophodnost tacnog izracunavanja delilaca. Sve se to uglavnom svodi na problem faktorizacije, a za jako velike brojeve to jeste problem. Prouci ovo: http://people.dmi.uns.ac.rs/~dockie/tb/lnotes/tb03.pdf Jedan lagan primer pronalazenja broja delilaca http://www.wikihow.com/Determi...mber-of-Divisors-of-an-Integer Ako zelis da se bavis problemima teorije brojeva onda ces morati malo vise da se pozabavis tom teorijom. Npr. krenes odavde Waclaw-Sierpinski-Elementary-Theory-of-Numbers [Ovu poruku je menjao igorpet dana 15.06.2013. u 19:51 GMT+1] [ number42 @ 15.06.2013. 18:53 ] @
Citat: Sve se to uglavnom svodi na problem faktorizacije upravo tako, a bas sam faktorizaciju hteo da izbegnem grafickim resavanjem. mada ne znam da li je na ovaj nacin moguce, cisto sumnjam... [ Bojan Basic @ 17.06.2013. 10:38 ] @
Citat: Bojan Basic: Ali OK, ako uzimamo u obzir samo kvadratne polinome po jednoj promenljivoj takve da daju proste vrednosti za sve vrednosti argumenta od  pa do što veće gornje granice (da li sam sad dovoljno restriktivan? :)), izraz pa do što veće gornje granice (da li sam sad dovoljno restriktivan? :)), izraz 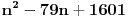 da je proste vrednosti za da je proste vrednosti za  u rasponu od u rasponu od  do do 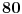 . .A inače, da se nadovežem na ovo. Priložiću dokaz da, ukoliko je tačna hipoteza o prostim  -torkama (a niko zaista ne sumnja u tačnost te hipoteze), tada za svaki prirodan broj -torkama (a niko zaista ne sumnja u tačnost te hipoteze), tada za svaki prirodan broj  postoji prirodan broj postoji prirodan broj  takav da izraz takav da izraz 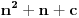 uzima proste vrednosti za sve uzima proste vrednosti za sve  u rasponu od u rasponu od  do do  ! !Za početak, da vidimo šta tvrdi hipoteza o prostim  -torkama. Za -torkama. Za  -torku nenegativnih celih brojeva -torku nenegativnih celih brojeva 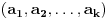 kažemo da je prihvatljiva ukoliko ne postoji prost broj kažemo da je prihvatljiva ukoliko ne postoji prost broj  takav da se u posmatranoj takav da se u posmatranoj  -torci javljaju svi mogući ostaci pri deljenju sa -torci javljaju svi mogući ostaci pri deljenju sa  . (Primera radi, trojka . (Primera radi, trojka 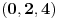 nije prihvatljiva jer sadrži sve ostatke pri deljenju sa nije prihvatljiva jer sadrži sve ostatke pri deljenju sa  , dok recimo trojka , dok recimo trojka 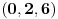 jeste prihvatljiva.) Hipoteza o prostim jeste prihvatljiva.) Hipoteza o prostim  -torkama tvrdi da za svaku prihvatljivu -torkama tvrdi da za svaku prihvatljivu  -torku -torku 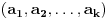 postoji beskonačno mnogo prirodnih brojeva postoji beskonačno mnogo prirodnih brojeva  takvih da su sve vrednosti takvih da su sve vrednosti 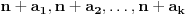 proste. proste.Vratimo se sada na dokaz najavljenog. Neka je dat prirodan broj  . Označimo . Označimo 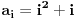 . Tvrdimo da je . Tvrdimo da je 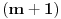 -torka -torka 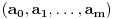 prihvatljiva. Zaista, primetimo najpre da su svi brojevi prihvatljiva. Zaista, primetimo najpre da su svi brojevi 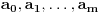 parni, pa prost broj parni, pa prost broj  ne narušava prihvatljivost. Neka je sada ne narušava prihvatljivost. Neka je sada  neparan prost broj, i pretpostavimo da on narušava prihvatljivost (tj. da se među brojevima neparan prost broj, i pretpostavimo da on narušava prihvatljivost (tj. da se među brojevima 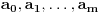 javljaju svi ostaci pri deljenju sa javljaju svi ostaci pri deljenju sa  ). Neka je ). Neka je  proizvoljan kvadratni neostatak po modulu proizvoljan kvadratni neostatak po modulu  koji pritom daje ostatak koji pritom daje ostatak  pri deljenju sa pri deljenju sa  (kako su brojevi (kako su brojevi  i i  uzajamno prosti, ovakva vrednost uzajamno prosti, ovakva vrednost  može se odabrati na osnovu kineske teoreme o ostacima), i označimo može se odabrati na osnovu kineske teoreme o ostacima), i označimo 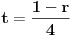 . Kako smo pretpostavili da . Kako smo pretpostavili da  narušava prihvatljivost, među brojevima narušava prihvatljivost, među brojevima 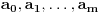 postoji neki, recimo postoji neki, recimo 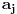 , koji je kongruentan sa , koji je kongruentan sa 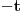 po modulu po modulu  . No, sada imamo . No, sada imamo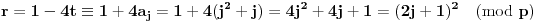 , ,a ovo je u kontradikciji s činjenicom da je  kvadratni neostatak po modulu kvadratni neostatak po modulu  . .Time smo pokazali da je 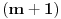 -torka -torka 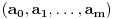 prihvatljiva. Odatle sledi da postoji prirodan broj prihvatljiva. Odatle sledi da postoji prirodan broj  takav da su svi brojevi takav da su svi brojevi 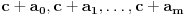 prosti. No ovi brojevi su upravo prosti. No ovi brojevi su upravo 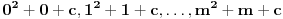 , tj. vrednosti izraza , tj. vrednosti izraza 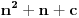 za za  u rasponu od u rasponu od  do do  . Kraj dokaza. . Kraj dokaza.Polinom 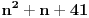 zapravo je ilustracija da za zapravo je ilustracija da za 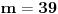 imamo imamo 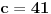 (mala ispravka, ranije smo komentarisali da posmatrani polinom uzima proste vrednosti do (mala ispravka, ranije smo komentarisali da posmatrani polinom uzima proste vrednosti do 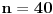 , zapravo je do , zapravo je do 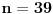 ). Da vidimo za koje ). Da vidimo za koje  izraz izraz 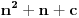 uzima proste vrednosti za uzima proste vrednosti za  u rasponu od u rasponu od  do do 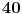 (tj. makar samo za jedan korak više od ovog što imamo). Odgovor je, nažalost, da ne znamo eksplicitno koliko (tj. makar samo za jedan korak više od ovog što imamo). Odgovor je, nažalost, da ne znamo eksplicitno koliko  iznosi. (Gornje tvrđenje kaže da takvo iznosi. (Gornje tvrđenje kaže da takvo  postoji — doduše kondicionalno, no korišćena pretpostavka je veoma verovatna — ali ne znamo ništa o tome koliko takvo postoji — doduše kondicionalno, no korišćena pretpostavka je veoma verovatna — ali ne znamo ništa o tome koliko takvo  mora biti veliko.) Zna se da traženo mora biti veliko.) Zna se da traženo  nije manje nije manje 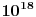 , ali verovatno je mnogo veće i od ove granice. , ali verovatno je mnogo veće i od ove granice.[ darkosos @ 17.06.2013. 11:00 ] @
Upravo sam se to zapitao, odnosno, da li postoji polinom drugog stepena koji bi "pohvatao" sve proste (to je vise od izlozenog ali slicna je ideja). Da li bi nesto slicno moglo da se izvede ako bi u pricu dodao i koeficijent uz linearan clan? Ovaj sto gadja do 80 je relativno prost - mada ne znam koliko je prosto dobijen... Ali kapiram da bi program brzo nasao ovo resenje preko svih kombinacija za b i c, sa trazenim uslovom.
[ Bojan Basic @ 17.06.2013. 12:09 ] @
Citat: darkosos: Upravo sam se to zapitao, odnosno, da li postoji polinom drugog stepena koji bi "pohvatao" sve proste (to je vise od izlozenog ali slicna je ideja). U kom smislu „pohvatao“? Hoćeš da sve vrednosti polinoma budu prosti brojevi, ili da se među svim mogućim vrednostima nađu svi prosti brojevi (i još gomila složenih, koje zanemarujemo), ili nešto treće? [ darkosos @ 17.06.2013. 12:22 ] @
Mislio sam u nastavku onog o cemu se ovde pricalo - dakle da je p(n) prost broj za sve prirodne n (plus 0).
[ Bojan Basic @ 17.06.2013. 13:16 ] @
[ number42 @ 17.06.2013. 15:38 ] @
kada covek pogleda koliko vremena su prosti brojevi nepoznanica, cisto sumnjam da ce moci da budu ukroceni standardnim nacinom razmisljanja i razradjivanja hipoteza i teorema. verovatno je potreban drugaciji pristup, ili mozda neko slucajno otkrije neku shemu.
ako uzmemo analogiju sa negativnim brojevima, vidimo da su oni hiljadama godina bili nepoznati. a koliko je tesko bilo setiti se da oduzmu 5-10 i da racunaju s tim? bas nimalo. nije problem u tome da su ti ljudi kroz istoriju bili glupi (npr stari grci koji nisu poznavali negativne) pa se nisu mogli setiti koncepta kao sto je negativan broj, ne, bili su izuzetno inteligentni, recimo jos od vavilona (a verovatno i sumera jer je znanje te civilizacije utopljeno u vavilonsko) su poznavali pitagorinu teoremu, a dokazali pretpostavlja se mnogo pre pitagore (sta je sve bilo u aleksandrijskoj biblioteci i iz kog perioda mozemo samo da nagadjamo). dakle, za otkrivanje negativnih brojeva su bili potrebni ljudi koji razmisljaju nestandardno, za otkrivanje nule u indiji su bili potrebni nestandardni nacini razmisljanja, i slicno je za ostale stvari. sta bi to u sadasnjem kontekstu znacilo da bi trebalo nestrandardno razmisljanje da bi se dobili zakljuchci? pa, ne bi se mnogo razlikovalo od nestrandardnog razmisljanja u proslosti koje je moglo da ubrza razvoj matematike i time uopste nauke. ovo je jako povezano sa drustvenim poretkom. standardno razmisljanje namece trenutni drustveni poredak u kome je potrebno resavati odredjene probleme, u potpunosti podredjen utilitarizmu. npr, vavilonu je bila neophodna pitagorina teorema zbog poljoprivrede i tacnog merenja zemljista. arhitektima piramida je bilo potrebno savrseno znanje geometrije, itd, gomila primera koji pokazuju da nauku guraju u onom smeru koji ce obezbediti najekonomicnije, najproduktivnije, funkcionisanje najvisih slojeva drustva. ukratko, namece se standardno razmisljanje koje donosi korist vodjama. da li je to u svim slucajevima... mislim da ne, ali ogromnom vecinom da. isti slucaj je danas kada se standardno ucenje, rezonovanje, zakljucivanje, razmisljanje podvodi pod sistematsko, a koje kao i u proslosti ima za cilj sto vecu korist vladajucih, ne samo matematika, vec i ostale nauke. a sistematsko rezonovanje ne dolazi samo po sebi, vec potice od sistematskog ucenja. a ono je isto na celom svetu, prilagodjeno tome da ljudi kada usvoje znanje razmisljaju na nacin koji ce posluziti nekome da zgrne bogatstvo. takvim sistemom edukacije proizvodi se gomila matematicara i naucnika koji ce za neke relativno dobre iznose novca nekome drugom donositi enormna bogatstva, prestiz, i moc. ovo razmisljanje je vrlo ispravno iz ugla industrijalaca i vlada, ali vrlo neispravno sustinski. iz vise razloga. prvo, danasnji sistem edukacije i kasnijeg rezonovanja izbacuje nekih 2% ljudi koji su nadareni za matematiku recimo. sta je sa ostalima? da li su ti ljudi glupi za tu oblast? ja mislim da ne, vec se taj nacin usvajanja znanja ne poklapa sa njihovim nacinom. i umesto da obrazovni sistem izbacuje 30 posto ljudi koji bi se bavili naukom i obezbedjivali veci profit shefovima, to je svedeno na neki mizeran procenat ukupne populacije. druga stvar je da, ako se ne bi nametao standardan tj sistematski pristup obrazovanju i kasnijem rezonovanju u nauci, to bi povecalo kapacitet kreativnog razmisljanja ljudi, a koje je kljucno pri stvaranju novih ideja, koncepata, dolazenja do resenja, i sl, a to opet znaci veci profit. dakle, ljudi koji iz koristi pristupaju oblikovanju nauke pa i matematike su vrlo kratkovidi, cak i za sopstvene standarde i vrednosti. e sad, kako izaci iz tog standardnog, sistematskog koloseka rezonovanja da bi se postigli neki bolji rezultati? jedan od nacina je kombinovanje matematike sa umetnoscu npr. o povezanosti matematike i muzike je mnogo pisano, a u slikarstvu je poigravanje perspektivom moglo da bude inspiracija gomili matematicara da su se setili toga, npr van gogov prikaz sobe neobicne perspektive i dimenzija inspirise dalija da napravi raspetog hrista sa potpuno neverovatnom perspektivom koja kao da stvara dodatni prostor, onda to recimo inspirise kreatore sf-a tako da u 'dr who' mozemo videti brod sa negativnom geometrijom, a koji je zatim prepisan u jednoj epizodi star treka. a sta je to negativna geometrija? danas nista. mozda sutra neko pocne iz zabave da se bavi ovim konceptima i onda se otkrije neka prakticna primena, u saradnji sa ostalim naukama. hocu da kazem, za resavanje mnogih stvari treba se pomeriti i sliku pogledati iz vece udaljenosti, na engleskom postoji sjajan izraz, otprilike 'to get out of the box". Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|