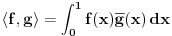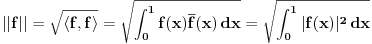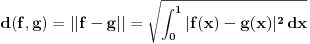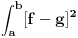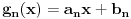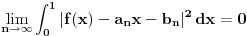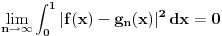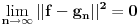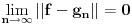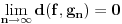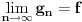[ Milosh Milosavljevic1 @ 15.06.2013. 22:49 ] @
|
[ Nedeljko @ 15.06.2013. 23:07 ] @
Standardni tipski zadaci. U čemu je problem? Za literaturu pitaj profesora.
[ Milosh Milosavljevic1 @ 15.06.2013. 23:12 ] @
Glavni problem je sto ne volim da ucim sablone bez nekog dubljeg znanja teorije. A sto se tice teorije koja pokriva ovo, literaturu nam sacinjava http://poincare.matf.bg.ac.rs/~milinko/skripta/Analiza2.pdf koja je jako teska za citanje i tumacenje (jer je pisana sa tom namerom), pa trazim neku literaturu koja je malo jasnije pisana, a pokriva ove oblasti.
[ Milosh Milosavljevic1 @ 15.06.2013. 23:17 ] @
A problem ovde(sto se konkretnih zadataka tice) je treci i deo cetvrtog zadatka( a i b sam resio, problem je v,g,d,dj).
[ Nedeljko @ 16.06.2013. 00:20 ] @
Ma, vidim, on je to hteo da zipuje, a onda je to malo upotrebljivo za učenje. Za učenje ne trebaju samo gole definicije i stavovi, već što više primera.
Koristi net za svaku temu ponaosob. Treći zadatak znači da nađeš neprekidne funkcije koje se mogu proizvoljno dobro srednjekvadratno aproksimirati linearnom funkcijom. Skup linearnih funkcija je konačnodimenzioni (dvodimenzioni) potptostor odgovarajućeg predhilbertovog prostora, pa je kao takav zatvoren potprostor, odnosno njegovom zatvorenju pripadaju samo njegove tačke, pa je traženi skup funkcija skup linearnih funkcija. U četvrtom su v i g nekorektno postavljeni, jer je X definisano na sferi, a ne na torusu, a preostali deo je zapravo površinski integral prve vrste. [ Milosh Milosavljevic1 @ 16.06.2013. 01:10 ] @
Znaci, ako sam dobro razumeo, za metriku u odnosu na koju posmatram uzimam gore dati integral razlike funkcija. E sad, posmatram skup svih linearnih funkcija oblika ax+b i ovu metriku. Oni zadaju jedan potprostor unitarnog prostora za koji mogu da uzmem recimo skup svih glatkih funkcija i gore pomenutu metriku. Sad iskoristim tvrdjenje da je zatvorenje pred Hilbertovog potprostora dimenzije 2 u stvari sam taj potprostor,sto bi dokazao tako sto pokazem da limes proizvoljnog niza linearnih funkcija iz tog potprostora pripada tom potprostoru u gore definisanoj metrici. A to je trivijalno jer radimo sa prostorom linearnih funkcija.
[Ovu poruku je menjao Milosh Milosavljevic1 dana 16.06.2013. u 02:22 GMT+1] [ Milosh Milosavljevic1 @ 16.06.2013. 03:03 ] @
Jos je za 3. ostalo da, posto mi inicijalno ne znamo da f ima bazu konacen dimenzije, onda pretpostavljam da treba da se integral razvije u red i da se i tu trazi neka kontradikcija.
[ Nedeljko @ 16.06.2013. 10:26 ] @
Ne. Znamo da je rastojanje od f do potprostora linearnih funkcija nula, odnosno da f pripada zatvorenju potprostora, a posto je potprostor dimenzije 2, njegovo zatvorenje je sam on, pa f pripada njemu.
[ Milosh Milosavljevic1 @ 20.06.2013. 22:39 ] @
Nedeljko, opet ja , nije mi najjasnije ovo resenje treceg zadatka. Nije mi jasno u kom prostoru i sa kojom topologijom posmatramo ovu zatvorenost? Ako uzmemo metriku koja je ovaj integral iz zadatka, kako znamo da ona indukuje normu, jer znamo da norma uvek indukuje metriku, al obrnuto ne mora da vazi. Jedina norma koju bi ova metrika mogla da indukuje je
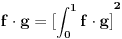 . . [ Nedeljko @ 20.06.2013. 23:15 ] @
[ Milosh Milosavljevic1 @ 20.06.2013. 23:27 ] @
[ Nedeljko @ 20.06.2013. 23:40 ] @
[ Milosh Milosavljevic1 @ 20.06.2013. 23:47 ] @
E hvala puno, to me je mucilo. Mislio sam da mogu da "izgubim" neke f-je zbog ovog korena, a ako uzmem kvadrat gubim nejednakost trougla i onda nemam metriku. Sad mi je u potpunosti jasno. Hvala jos jednom.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|