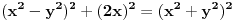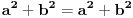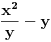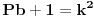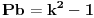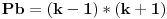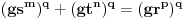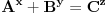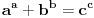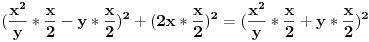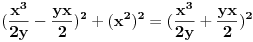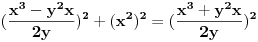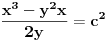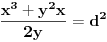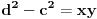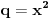[ number42 @ 20.06.2013. 12:01 ] @
|
[ miki069 @ 20.06.2013. 13:12 ] @
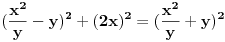 Posle nalaženja zajedničkog i množenja sa y^2 "Pitagora" se pretvara u: 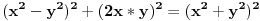 Što posle kvadriranja izraza pretvara "Pitagoru" u 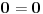 Dakle tačna je jednakost. U generisanju ima uslov da je y delilac od x^2. Ko je poznata, a ko nepoznata? Koje vrednosti uzima poznata u generatoru? [Ovu poruku je menjao miki069 dana 20.06.2013. u 15:46 GMT+1] [ darkosos @ 20.06.2013. 13:44 ] @
@miki069
Nedostaje ti samo y u drugoj zagradi. I to je onda opsti oblik koji je ovde sesnajst puta navodjen. [ number42 @ 20.06.2013. 13:45 ] @
e to majstore, to je to
samo mala ispravka jednacini, dodaje se y u drugi clan. znaci oblik je 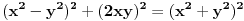 e sad, sta je zanimljivo- ovo bi trebalo da radi za svako x i y. medjutim prvi clan, ako je prost broj (Pb), se ne moze izraziti kao razlika kvadrata, osim ako je y=1. i onda normalno dobijas neke brojeve za pitagorinu teoremu. iz ovoga bi sledilo da za svako Pb+1 koje nije kvadrat celog broja, Pb ne moze biti kateta pravouglog trougla. recimo 7 (7+1 nije kvadrat), 17 (17+1 nije kvadrat), itd. ako ne gresim negde u rezonovanju, nisam znao za ovo, a bas je interesantno. [Ovu poruku je menjao number42 dana 20.06.2013. u 14:58 GMT+1] [ number42 @ 20.06.2013. 14:03 ] @
ako negde gresim u rezonovanju neka slobodno neko ukaze, jer nista slicno o ovome nisam cuo do sada.
znaci prost broj, koji sabran sa jedinicom nije kvadrat, ne moze biti kateta u pt... svasta... [ Nedeljko @ 20.06.2013. 14:34 ] @
[ number42 @ 20.06.2013. 14:51 ] @
[ number42 @ 20.06.2013. 15:33 ] @
da, u pravu si, moj previd.
y mora biti za jedan manje od x da bi to bio prost broj. (x-y)(x+y)=1*(x+y). i on mora biti jednak x+y, ako radimo preko druge jednacine, tj razlike kvadrata. al opet se dobijaju dve ekvivalentne tvrdnje iz ove dve jednacine koje povezuju proste sa celim na neki nacin, a upravo sam to trazio prvom jednacinom... samo ne znam kako se povezuju. [ Nedeljko @ 20.06.2013. 16:25 ] @
Imam jedno pitanje za sve osim postavljaca teme. Da li vas ova tema podseca na Sprecine mudrolije sa transformisanjem izraza?
[ number42 @ 20.06.2013. 19:02 ] @
sada posmatram drugu jednacinu, i dobija se zanimljiva stvar ako sve clanove pomnozimo sa pi
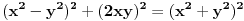 dobijamo formule za povrsinu kruga i obim kruga, i imamo 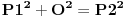 prema ovome, iz formule sledi da nikada ne mozemo imati da je zbir kvadrata dva kruga jednak kvadratu nekog treceg, ako su im precnici celi brojevi. tj 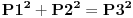 je nemoguce ako su r1, r2 i r3 celi brojevi. je nemoguce ako su r1, r2 i r3 celi brojevi.ako sve clanove sada podelimo sa pi, onda dobijamo da nikada ne mozemo imati 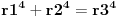 , ako su r-ovi celi brojevi. , ako su r-ovi celi brojevi.i eto laganog dokaza za fermatovu teoremu za n=4 ne znam da li se ovom metodom moze doci do vecih stepena od 4... [ miki069 @ 21.06.2013. 11:09 ] @
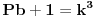 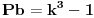 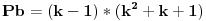 Ovim si "dokazao" Fermatovu teremu za n=3. 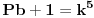 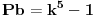 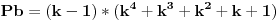 Ovim si "dokazao" Fermatovu teremu za n=5. 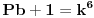 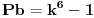 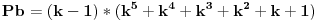 Ovim si "dokazao" Fermatovu teremu za n=6.... Nije mi jasno kakve veze ima Fermatova teorema sa Pb+1? I kakve veze ima sa čuvenim "opštim" oblikom Pitagorine teoreme da je 0=0? [Ovu poruku je menjao miki069 dana 21.06.2013. u 13:14 GMT+1] [ number42 @ 21.06.2013. 16:09 ] @
@miki069,
Pb nije ista oznaka kao i P. Pb je prost broj, a P je povrsina. mozda sam nedovoljno naglasio distinkciju pa je dovelo do nerazumevanja. nego, evo jos jedne stvari. imamo dokazano da je nemoguce 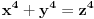 . drugim recima, za bilo koje celo x, ne postoje celi brojevi y i z za koje je formula tacna. . drugim recima, za bilo koje celo x, ne postoje celi brojevi y i z za koje je formula tacna.to je za stepen 4. ako hocemo dalje da ispitamo za stepen 8, onda napravimo zamenu 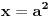 . .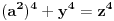 ali kako smo videli da y i z ne mogu biti celi brojevi a da je jednacina tacna, onda oni ne mogu biti ni stepeni celih brojeva. dakle, 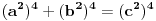 nije tacno. nije tacno. ako sad uvedemo zamenu 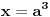 u prvu netacnu jednacinu dobijamo u prvu netacnu jednacinu dobijamo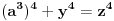 a kako, opet, y i z ne mogu biti celi brojevi, onda ne mogu biti ni stepeni celih brojeva, u konkretnom slucaju 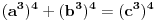 itd, za bilo koji stepen koji uzmemo. kako y i z nisu celi brojevi, onda oni nece biti stepen nijednog broja. uopsteno, to je 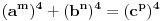 ili 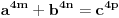 kako je fermatova dokazana za sve stepene a ne samo 4, onda je jos opstiji oblik jednacine 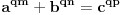 i ona je nemoguca. i ona je nemoguca.ovo bi se moglo opisati: jednacina je nemoguca kada su osnove razliciti celi brojevi, a stepeni imaju jednog delioca koji je isti. medjutim, evo opovrgavanja ovoga. bilova hipoteza http://en.wikipedia.org/wiki/Beal's_conjecture tvrdi da je jednacina oblika 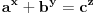 tacna kada osnove (a,b, i c) imaju jednog zajednickog delioca. ovo je i potvrdjeno racunarski do 1000 cini mi se za promenjive. tacna kada osnove (a,b, i c) imaju jednog zajednickog delioca. ovo je i potvrdjeno racunarski do 1000 cini mi se za promenjive.a to je suprotno zakljucku koji sam malopre napisao. jedina mogucnost je da gresim u izvodjenju, ali ne znam u kom delu? [ number42 @ 22.06.2013. 16:28 ] @
i, jel neko zna odgovor iz prethodnog komentara?
[ Nedeljko @ 22.06.2013. 16:35 ] @
Znaju Bojan Basic, darkosos, miki069, Nedeljko, Sonec...
Pravo je pitanje ima li zainteresovanih za odgovaranje. [ number42 @ 23.06.2013. 00:42 ] @
zaboravio sam da naglasim u ovom komentaru iznad gde sam postavio pitanje
http://www.elitesecurity.org/t466525-0#3312913 dakle, smena koju uvodim ( 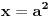 )je pretpostavka. )je pretpostavka. znaci pretpostavljam istinitost te tvrdnje (da je 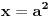 ) da bih dosao do kontradikcije u jednacini. prvoj, a nadalje i ostalim. ) da bih dosao do kontradikcije u jednacini. prvoj, a nadalje i ostalim. moze i konkretno, x je recimo 4, a je 2. x je 27, a je 3, kada je smena 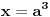 sta god da uvedem kao smenu umesto x, dobija se kontradikcija. dakle, bilo koji ceo broj na bilo koji ceo stepen, daje ostatak jednacine kao nemoguc, a jednacinu kao netacnu. (a to je u saglasnosti sa fermatovom teoremom). ali kada se postupak nastavi, onda je u nesaglasnosti sa celom bilovom hipotezom (a koja je potvrdjena kolike su mogucnosti racunara)?! [ number42 @ 23.06.2013. 12:20 ] @
otkrio sam i drugu mogucnost sta bi moglo da bude sa kontradikcijom u ovom slucaju. ne znam koliko ovo izgleda sve zapetljano sada, nadam se da nije.
dakle iz fermatove teoreme sam dobio: 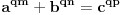 tu postoji mogucnost da postupak u nekom delu nije tacan. ali, ako je postupak tacan, dobija se da je u suprotnosti sa bilovom hipotezom koja tvrdi da jednacina oblika a^x+b^y=c^z tacna kada osnove imajju jednog zajednickog delioca. kada se bilova hipoteza primeni na gornju jednacinu, dobija se oblik: 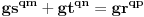 a kako je bilova hipoteza ispitana racunarski za nekih prvih valjda hiljadu brojeva za promenjive, moguce je da se ne nailazi na ovaj oblik, tj da za prvih 1000 ne postoje promenjive koje ispunjavaju ove uslove, tako da nisu ni mogli da naidju na netacnost. ako je tacan postupak izvodjenja, onda ne ispunjava uslove ni za jedan slucaj promenjivih, to jest bilova hipoteza je netacna. a nagrada za potvrdu ili negiranje bilove hipoteze je milion dolara... znaci, ili sam pogresio u izvodjenju, a to je veca verovatnoca ako neko moze da mi ukaze gde gresim u izvodjenju- placam suvim zlatom [ number42 @ 23.06.2013. 13:13 ] @
[ Bojan Basic @ 23.06.2013. 13:19 ] @
[ number42 @ 23.06.2013. 13:34 ] @
tz... covece srusio si mi snove, taman sam mislio da uzmem milionce
i izgledalo mi je previse jednostavno, znaci greska je bila u tome da nisam dobro skontao bilovu hipotezu (a na zalost nije prevedena sa engleskog pa verovatno zbog toga). pa pretpostavljam da se moze izvuci zakljucak iz ove dve jednacine iznad, da, ako je bilova hipoteza tacna- onda njeni stepeni ne mogu da imaju zajednickog delioca (ocigledno, jer se onda svodi na fermatovu teoremu). [ darkosos @ 23.06.2013. 14:20 ] @
[ number42 @ 23.06.2013. 14:35 ] @
pa jesam kao preveo na temi "beal's conjecture", ali uopste nisam bio siguran da li je prevod tacan, pa sam zaboravio nakon tri sekunde.
evo jednog specijalnog slucaja bilove hipoteze, jako zanimljivo: 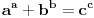 je nemoguce. jer ako je tacno, onda osnove moraju imati jednog zajednickog delioca. a kako su osnove i stepeni isti, onda i stepeni moraju imati jednog zajednickog delioca, a to se onda svodi na fermata. ne znam da li postoji dokaz da je ova jednacina (ne)moguca. [ darkosos @ 23.06.2013. 14:41 ] @
Ali mora da si onda opet "preveo", cim si koristio ovde... Jako zanimljivo...
I opet ovde pogresno kostis izraz "Bilova hipoteza". [ number42 @ 23.06.2013. 15:00 ] @
[ miki069 @ 23.06.2013. 15:03 ] @
Citat: number42: sada posmatram drugu jednacinu, i dobija se zanimljiva stvar ako sve clanove pomnozimo sa pi 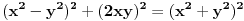 dobijamo formule za povrsinu kruga i obim kruga, i imamo 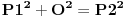 prema ovome, iz formule sledi da nikada ne mozemo imati da je zbir kvadrata dva kruga jednak kvadratu nekog treceg, ako su im precnici celi brojevi. tj 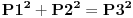 je nemoguce ako su r1, r2 i r3 celi brojevi. je nemoguce ako su r1, r2 i r3 celi brojevi.ako sve clanove sada podelimo sa pi, onda dobijamo da nikada ne mozemo imati 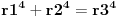 , ako su r-ovi celi brojevi. , ako su r-ovi celi brojevi.i eto laganog dokaza za fermatovu teoremu za n=4 :) Stvarno ne razumem ovaj "lagani" dokaz Fermatove teoreme za 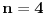 , a pokušavam. , a pokušavam.Krenuo si od čuvene "opšte" Pitagorine teoreme da je 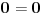 . .Onda je množiš sa pi i pojavljuju se površine kruga1 i kruga 2: 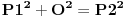 Obim je od koje kružnice: prve, druge ili neke treće? Čak mi nije ni jasno štoj je taj član obim. Ako važi ta veza površina kruga1 i kruga 2 i obima nekoga, zašto "nikada" ne važi: 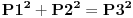 ? ?"nekad" i "nikad" su dosta različiti pojmovi. Negacija od "za svako x važi tvrđenje T(x)" glasi "postoji x da ne važi T(x)", a ne "za svako x ne važi T(x)". Ili mi je nešta promaklo u prvom delu gde je objašnjavan generator Pitagorinih trojki. Jel generator uspeo i kako glasi? Ili nije uspeo za neke? Zbog onog Pb+1. Stvarno mi ništa nije jasno. [ number42 @ 23.06.2013. 15:15 ] @
@miki069,
"opsta pitagorina teorema" znaci da za sve moguce vrednosti x i y, ona izbacuje sve moguce vrednosti clanova pitagorine teoreme, i suprnotno. dakle uneses bilo koje brojeve u jednacinu pt, i uvek mozes da je izrazis u opstem obliku s dve promenjive. za krugove, 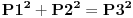 je nemoguce jer kada svaki clan podelis sa pi, dobijas fermatovu teoremu cetvrtog stepena. je nemoguce jer kada svaki clan podelis sa pi, dobijas fermatovu teoremu cetvrtog stepena.[ miki069 @ 23.06.2013. 16:15 ] @
Mislim na "generator" svih celobrojnih Pitagorinih trojki, sa kojim je sve i počelo.
Taj generator: postoji ili ne postoji? Ako postoji kako glasi? Ako Fermatova teorema važi onda za krugove ne važi 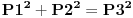 . To je jasno. . To je jasno.Bilo je napisano: pošto za krugove ne važi 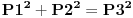 onda je "lagano" dokazana Fermatova teorema za n=4. onda je "lagano" dokazana Fermatova teorema za n=4.Implikacija i ekvivalencija uopšte nisu isto. Šta bi sa obimom? Kako je onaj član bio obim i zašto ako važi (ili ne važi) odnos 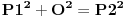 onda ne važi onda ne važi 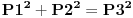 ? ?Obim i povrišina nisu uopšte isto. [ darkosos @ 23.06.2013. 16:34 ] @
[ number42 @ 23.06.2013. 17:05 ] @
Citat: miki069: Mislim na "generator" svih celobrojnih Pitagorinih trojki, sa kojim je sve i počelo. ne znam gde je sve tako pocelo, na ovoj mojoj temi nije mozes li da citiras gde sam to napisao? Citat: miki069: Šta bi sa obimom? obim, 2xy, se, pomnozen sa pi moze napisati kao 2xy*pi. ako zamenimo xy sa r, dobijamo 2r*pi, a to je obim. iz ovoga dobijemo kako da izrazimo x, i onda ga zamenimo u prvi clan. nakon malo sredjivanja, vidimo da se izraz koji dobijamo ne poklapa sa prvom opstom jednacinom pt koju sam dao na samom pocetku u prvom komentaru, a to je dokaz nemogucnosti transformacije O iz drugog clana u bilo koje P u uslovima opste pitagorine teoreme. dakle, dovoljno je da ne vazi za jedan clan, i da bude potvrdjeno da je nemoguce za celu jednacinu, a u ovom slucaju govorimo o 4. stepenu fermatove jednacine. ako jos nesto nije jasno slobodno pitaj ili me ispravi, nije nikakav problem. samo nemoj nesto kilometarski da racunam ne mogu se snaci s latexom nikako [ number42 @ 23.06.2013. 17:14 ] @
@darkosos,
cenim da zelis da odgovoris na moje pitanje, pa ako mozes ukratko da objasnis svoju tvrdnju za koju sam te pitao pre par komentara, a koja proizilazi iz bilove hipoteze: pa i ako si pogresio, a pretpostavljam da jesi, mislim nije problem, nigde ne pise da u izvodjenju, razmisljanju, nadogradnji znanja i slicno sve mora biti savrseno precizno u matematici. ipak smo ljudi a ne masine, a ovo je ono sto nam kao ljudima, kroz multiplikaciju kombinacija u razmisljanju, daje kreativnost i ideje. [ miki069 @ 23.06.2013. 19:16 ] @
Ajde vidi ko je i na kojoj temo ovo napisao. Ja nisam.
Citat: number42: pitanje je sledece: kako mozemo napisati pitagorinu teoremu pomocu 2 promenjive tako da ona uvek generise clanove koji su celi brojevi za sve kombinacije koje pt moze da ima? nasao sam jedan nacin 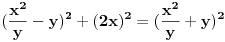 gde je gde je  deljivo sa y, a i jedno i drugo (x i y) su celi brojevi. deljivo sa y, a i jedno i drugo (x i y) su celi brojevi. ova formula generise svaku mogucu kombinaciju celih brojeva u pt, cak mislim da radi i sa negativnim vrednostima promenjivih, nisam bas nesto proveravao. Piše lepo da ova formula generiše svaku moguću kombinaciju celih Pitagorinih brojeva. Dakle pitanja su: 1. Gore navedena formula: a) generiše sve Pitagorine celobrojne trojke. b) ne generiše nikakve Pitagorine celobrojne trojke. c) nekada generiše, a nekada ne generiše Pitagorine celobrojne trojke. 2. Proizvod 2*x*y*pi je obrazac za obim: a) prvog kruga b) drugog kruga c) nekog trećeg kruga. Tačno je samo a nili b nili c. Za račun ne brini, nije mi problematičan. [Ovu poruku je menjao miki069 dana 23.06.2013. u 21:37 GMT+1] [ number42 @ 23.06.2013. 20:43 ] @
@miki069,
da, pa vidis razliku izmedju tvog navoda i citata. al, ok, sustina je tu negde ista... e sad, nisam siguran o cemu govoris, da li mislis da je formula (prva, s kojom sam poceo temu) netacna? nije problem, ako je greska mozes mi pokazati neki primer za koji ne vazi. kako sam ja izracunao, tacna je. za obim, u drugoj opstoj formuli pt ako clanove pomnozimo sa pi, onda je poluprecnik obima u drugom clanu x*y. nisam isao izracunavanjem odnosa tog poluprecnika i poluprecnika povrsina drugih krugova kako si postavio pitanja, mozda to ima neku poentu ali ja je ne vidim. isao sam, kako sam vec objasnio, izracunavanjem x iz drugog clana, i zamenom u prvi clan. dobija se oblik prve jednacine, u kome svi clanovi ne mogu biti povrsine krugova. sve se podeli sa pi, i dobije se nemogucnost za 4. stepen clanova. [ miki069 @ 23.06.2013. 23:03 ] @
X se ne može izraziti iz "drugog člana".
Može samo iz neke jednačine. Iz koje? [ number42 @ 24.06.2013. 00:27 ] @
[ number42 @ 25.06.2013. 00:28 ] @
evo da pokusam jos jednom ovaj kraj, mislim- da pokusam jer kad nazvrljam u svesci sve je ok, al kad racunam kroz latex onda ne mogu da se snadjem.
EDIT: greska, pokusacu ponovo [ darkosos @ 25.06.2013. 09:07 ] @
@number42
Ne odgovaram zato sto si po ko zna koji put pogresno protumacio moje reci. I nekako mi vec dosadilo... Pokusao sam da ti kazem da si na pogresno mesto stavio "za svako x", a ti si nekako skontao da sam je uradio nekakvu transformaciju. Na jednoj drugoj temi sam rekao "matematicki polupismeni" a ti si razumeo da ne znaju da pisu. Itd, ima toga jos... Elem, kad sam vec prozvan, moram da citiram sebe: Citat: I opet ovde pogresno kostis izraz "Bilova hipoteza". Kako si ti iz ovoga zakljucio da mislim: Najprostije receno, mislim da brkas sledece izraze: "Bilova hipoteza" i jednacina 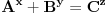 i gde god se pojavi ova jednacina ti kazes ono prvo :) Prosto neverovatno... Dakle, kada pricas o tome da li je jednacina moguca ili ne, ti ne pricas o BH, vec o toj jednacini. Jer, kao sto rekoh, BH ne utvrdjuje egzistenciju resenja ove jednacine, vec samo sta bi trebalo da vazi ako je jednacina tacna za neke A,B,C,x,y,z. i gde god se pojavi ova jednacina ti kazes ono prvo :) Prosto neverovatno... Dakle, kada pricas o tome da li je jednacina moguca ili ne, ti ne pricas o BH, vec o toj jednacini. Jer, kao sto rekoh, BH ne utvrdjuje egzistenciju resenja ove jednacine, vec samo sta bi trebalo da vazi ako je jednacina tacna za neke A,B,C,x,y,z.[ miki069 @ 25.06.2013. 09:20 ] @
Ne moraš da se smaraš sa računom.
Samo me interesuje iz koje jednačine si izrazio X? [ number42 @ 25.06.2013. 15:37 ] @
[ darkosos @ 25.06.2013. 20:10 ] @
@number42
Jos jednom, uopste nisam komentarisao tvoj zakljucak - ni da je ispravan ni da nije... I dalje to ne cinim. Nekako se slova koja napisem pretvaraju u nesto drugo prilikom citanja? Videcu sa moderatorima sta to nije u redu... [ number42 @ 25.06.2013. 21:20 ] @
@darkosos,
naravno da mozes da razgovaras sa kim zelis o cemu zelis, tvoja stvar, ne vidim nista sporno u tome. a za formulu 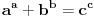 koja iz bilove hipteze proizilazi kao netacna, nisam bio siguran u ovo kada je a=2*Pb1, b=2Pb2, c=2Pb3 jer se u tom slucaju svodi na jednacinu pitagorine teoreme i trebalo bi da hipoteticki postoji mogucnost da je tacna. koja iz bilove hipteze proizilazi kao netacna, nisam bio siguran u ovo kada je a=2*Pb1, b=2Pb2, c=2Pb3 jer se u tom slucaju svodi na jednacinu pitagorine teoreme i trebalo bi da hipoteticki postoji mogucnost da je tacna. medjutim, kada je transformisemo u jednacinu pitagorine teoreme pa svaki clan podelimo sa 2_na_najmanji_stepen koji imamo u nekom od tri clana, dobijamo clanove pitagorine teoreme koji su paran i neparan sa leve strane jednakosti, i paran s desne strane jednakosti. a to je u suprotnosti sa pitgorinom teoremom. tako da 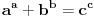 vazi kao netacna za sve brojeve, ako je bilova pretpostavka tacna. vazi kao netacna za sve brojeve, ako je bilova pretpostavka tacna.[ darkosos @ 25.06.2013. 21:26 ] @
@number42
Hvala ti puno... Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|