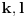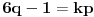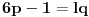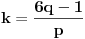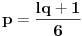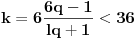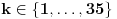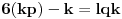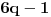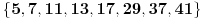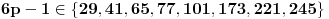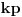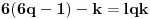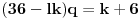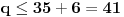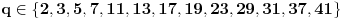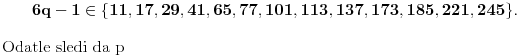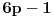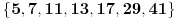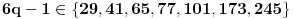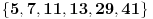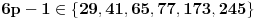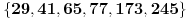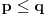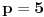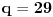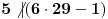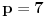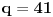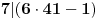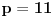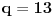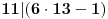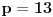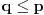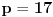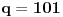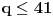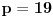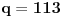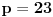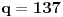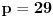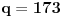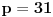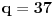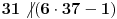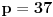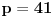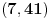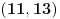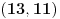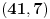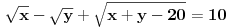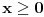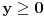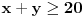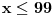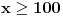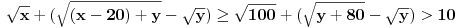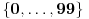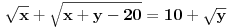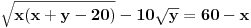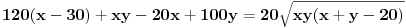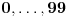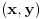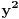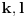
Dakle, postoje prirodni brojevi takvi da je

(1) ,
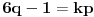
(2) .

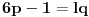
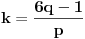
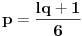
Iz jednačine (1) je , a iz (2) , pa je

,

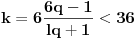
odnosno .

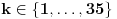
Množenjem jednačine (2) sa dobija se

.
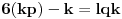
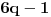
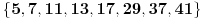
Odatle sledi da kao prost delioc broja ne veći od 41 pripada skupu , pa .

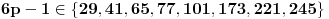
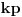
Zamenjujući tu iz prve jednačine je

,
,

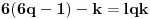
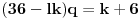
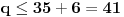
odakle je . Isti zaključak se izvodi za na analogan način, jer su uslovi zadatka simetrični. Dakle,

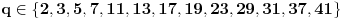
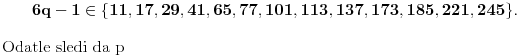
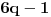
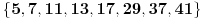
, odnosno kao prost delioc broja ne veći od 41 pripada skupu , pa .

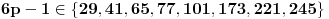
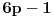
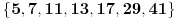
Odatle sledi da kao prost delioc broja ne veći od 41 pripada skupu , pa .

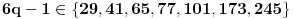
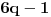
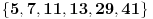
Odatle sledi da kao prost delioc broja ne veći od 41 pripada skupu , pa .

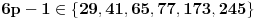
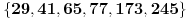
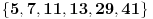
No, skup prostih brojeva ne većih od 41 koji su delioci bar jednog broja iz skupa je upravo , pa ovde stajemo sa ovim delom postupka. i idemo na isprobavanje. Obzirom da su uslovi simetrični po i , možemo se ograničiti na traženje onih rešenja kod kojih je .

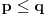
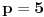
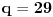
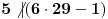
Ako je , onda je , ali , pa ova mogućnost otpada.

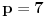
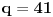
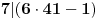
Ako je , onda je , pa pošto , jedno od rešenja je , .

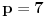
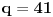
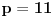
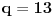
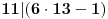
Ako je , onda je , pa pošto , jedno od rešenja je , .

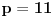
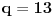
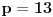
Ako je , onda je prost delilac broja 77, što je u suprotnosti sa .

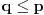
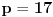
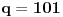
Ako je , onda je , što je u suprotnosti sa .

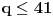
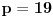
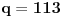
Ako je , onda je , što je u suprotnosti sa .

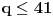
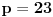
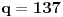
Ako je , onda je , što je u suprotnosti sa .

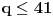
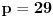
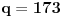
Ako je , onda je , što je u suprotnosti sa .

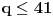
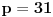
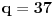
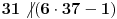
Ako je , onda je , ali , pa ova mogućnost otpada.

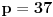
Ako je , onda je prost delilac broja 221, što je u suprotnosti sa .

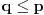
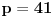
Ako je , onda je prost delilac broja 245, što je u suprotnosti sa .

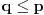
Dakle, rešenja su parovi , , , .

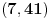
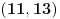
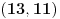
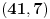
Što se drugog zadatka tiče, prvo izrazi preko prve jednačine, a onda to uvrsti u drugoj.

.

Najpre treba primetiti da potkorene veličine moraju biti nenegativne da bi koreni bili definisani, odnosno , , . Odmah se može zaključiti da je . U suprotnom bi bilo , a samim tim i



suprotno datoj jednačini. Dakle, za ima konačno mnogo mogućnosti (pripada skupu ).

Nastaviću kasnije.

Jednačina se može napisati u obliku

.

Kvadriranjem ove jednačine i sređivanjem dobijamo

.

Ponovnim kvadriranjem i sređivanjem dobijamo

.

Ponovnim kvadriranjem dobijamo kvadratnu jednačinu po . Zamenom u jednačini vrednostima i rešavanjem jednačine nalazimo parove koji su kandidati za rešenja. Da bismo proverili da li su rešenja, treba proveriti da li "prolaze unatrag" kroz oba procesa kvadriranja. Naime, kvadrati različitih brojeva mogu biti jednaki samo ako su ti brojevi suprotnog znaka.

Hvala Vam puno, puno... Stvarno ste mi puno pomogli..
Samo, ako mogu da pitam za ovaj drugi zadatak... Dakle, ovu poslednju jednakost ponovo kvadriram i uvrstavam sve vrijednosti x od 0 do 99... Ako sam ja to dobro razumila... Ali, ja kad kvadriram, meni se bas zakomplikuje izraz... :(

Grupiši šta ide uz , šta uz , a šta uz slobodni član. To su konstante.

Prilažem izvorni kod programa koji mi je našao sva rešenja.

x = 36
y = 0
z = 16

x = 60
y = 60
z = 100

x = 64
y = 100
z = 144

x = 81
y = 900
z = 961

Hvala Vam puno na ulozenom trudu i potrosenom vremenu...