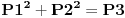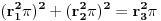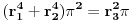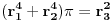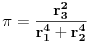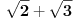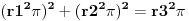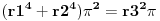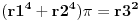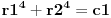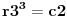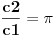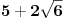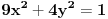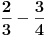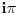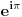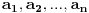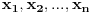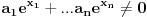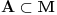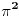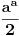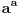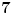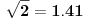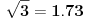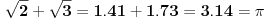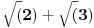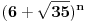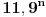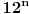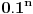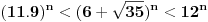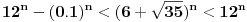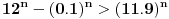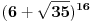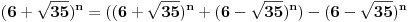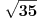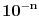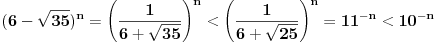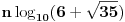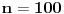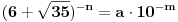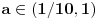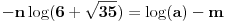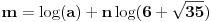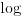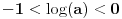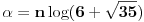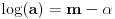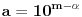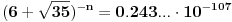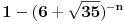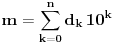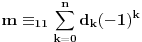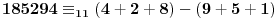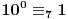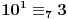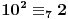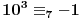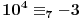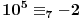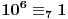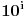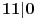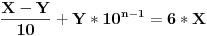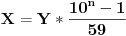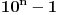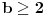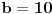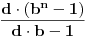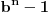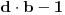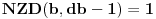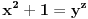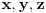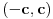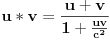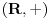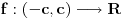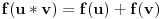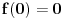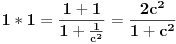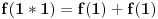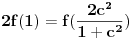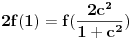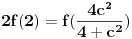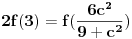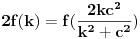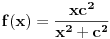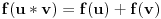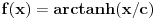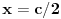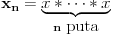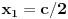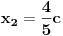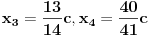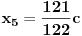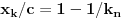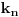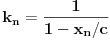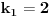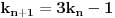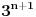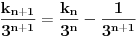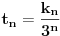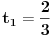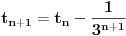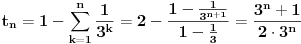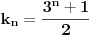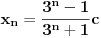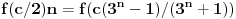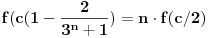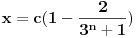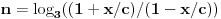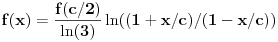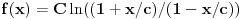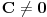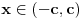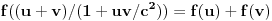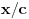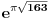|
|
[ number42 @ 03.07.2013. 19:24 ] @
|
| ovo je kao neki sled zadataka gde je cilj da se odgovori u roku od 24 casa. a moze i za 5 minuta ako je zadatak lagan.
znaci neko postavlja neki zadatak ili matematicku tvrdnju sa resenjem, i pitanjem da li je tacno ili netacno. ko odgovori, preuzima dalje i daje svoju postavku sa istim pitanjem na kraju.
znaci nije cilj da se odgovori samo sa da ili ne, vec i da se objasni zbog cega.
ako niko ne odgovori za 24 casa onda onaj koji je postavio treba da otkrije da li je tacno ili ne i kako je dosao do toga.
ne mogu hipoteze jer nisu proverljive, i ne moze neko dvaput za redom da postavlja, a moguce su postavke od elementarno prostih koje se resavaju za 2 minuta, do jako slozenih za koje je potrebno malo vise razmisljanja.
samo se stavi naslov u komentaru koji je broj pitanja da ne bi bilo zabune... i, to je sve.
|
[ number42 @ 03.07.2013. 19:27 ] @
evo nesto lagano za pocetak.
ako je P oznaka za povrsinu kruga, a poluprecnici su celi pozitivni brojevi, onda
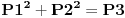
tacno ili netacno? [ Nedeljko @ 03.07.2013. 22:35 ] @
Baš me zanima da li postavljač zna da reši ovaj zadatak do kraja.
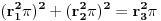 ,
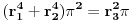 ,
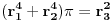 ,
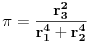 .
Dakle, zadatak je ekvivalentan pitanju da li se broj  može predstaviti kao količnik kvadrata prirodnog broja i zbira četvrtih stepena para prirodnih brojeva. Negativan odgovor sledi iz činjenice da je broj  iracionalan. Jedino ne znam da li bi postavljač to znao da dokaže. [ Nedeljko @ 03.07.2013. 22:37 ] @
Evo, da preuzmem štafetu.
Da li je broj 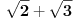 racionalan ili iracionalan?
Uputstvo: Sabrati 1.41 i 1.73. [ number42 @ 04.07.2013. 00:14 ] @
evo ostao sam duzan odgovor na prvo pitanje, a kako sam rekao da je lagan pa da ga lagano objasnim, a otprilike je za neki 7. razred osnovne.
znaci imamo postavku
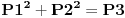
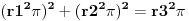
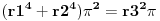
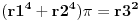
sada uvedemo zamenu, i to
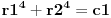
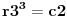
gde su c1 i c2 celi brojevi i dobijamo
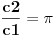
a kako razlomak po definiciji ne moze biti iracionalan broj, to je pocetna tvrdnja netacna. [ number42 @ 04.07.2013. 00:30 ] @
za ispitivanje iracionalnosti izraza
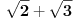
dovoljno je da ga kvadriramo i dobijamo
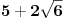
koji je iracionalan. a kako kvadrat razlomka ne moze dati iracionalan broj, to je i pocetni izraz iracionalan. [ number42 @ 04.07.2013. 00:35 ] @
i evo ga trece pitanje.
ako imamo samo lenjir i sestar (i olovku i papir  ), da bi odredjeni krug podelili na tri dela- dovoljno je da pre toga konstruisemo samo jedan trougao.
tacno ili ne? [ Nedeljko @ 04.07.2013. 00:37 ] @
To što si napisao kao rešenje zadatka je isto ono što sam i ja napisao, samo što si napravio jednu grešku u kucanju. U poslednjem redu umesto kuba treba kvadrat. Međutim, nisi odgovorio na ključno pitanje da li znaš da dokažeš ovo na šta se pozivaš - da je broj  iracionalan. [ Nedeljko @ 04.07.2013. 00:39 ] @
Ne treba da konstruišemo nijedan trougao da bismo dobili logo za mercedes.
[ number42 @ 04.07.2013. 06:35 ] @
evo da obrazlozim trece pitanje.
netacno je, recimo za podelu kruznice je dovoljan i sestar.
prethodno moramo znati- ako se u krug ucrta pravilan sestougao, on ima osobinu da mu je stranica jednaka poluprecniku kruga, a temena koja dodiruju kruznicu je dele na sest jednakih delova. i kad to znamo, onda je lako.
imamo znaci neki krug koji treba da podelimo na tri dela. otvor sestara namestimo na poluprecnik kruga, i onda podjemo od bilo koje tacke kruznice i sestarom na kruznici nacrtamo drugu tacku, onda iz druge trecu, itd. sada imamo kruznicu sa 6 tacaka koje je dele na sest jednakih delova. iz svake druge tacke povucemo pravu do centra kruga, i imamo tri jednaka dela.
[ number42 @ 04.07.2013. 06:38 ] @
i da potsetim, svako moze da postavi zadatak, slobodno se ne ustrucavajte. samo postavite neko resenje zadatka, i na kraju da li je tacno ili ne, i redni broj zadatka na ovoj temi u naslovu, da ne bi bilo zabune.
i nema veze koliko je lak ili tezak, uglavnom imamo limit od 24 casa za resavanje.
[ brux002 @ 04.07.2013. 09:00 ] @
Ako je udaljenost tacke T elipse
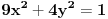
do jednog njenog fokusa jednaka 0,75.
Da li je tacno da je udaljenost do druge tacke veca od udaljenosti od prve tacke?
EDIT
Sad sam te video da pitanje mora biti u formi tacno/netacno.
Elem preformulisao sam.
[Ovu poruku je menjao brux002 dana 04.07.2013. u 10:23 GMT+1]
[Ovu poruku je menjao brux002 dana 04.07.2013. u 10:23 GMT+1][ darkosos @ 04.07.2013. 09:23 ] @
Po definiciji elipse, zbir rastojanja svake njene tacke do fokusa je fiksan i jednak je velikoj osi elipse (2a). Prema tome, odgovor je 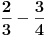 .
EDIT: sad sam video da je ovo nemoguce :) a i da je preformulisano pitanje... [ djoka_l @ 04.07.2013. 09:41 ] @
Ova elipsa je "zarotirana" tako da je 2a=1 (po y osi), pa je rastojanje 0.25
http://www.wolframalpha.com/input/?i=9x%5E2%2B4y%5E2%3D1+foci[ darkosos @ 04.07.2013. 09:55 ] @
E, jes, nisam provalio da je "a" manje "b"...
[ Milosh Milosavljevic1 @ 04.07.2013. 15:20 ] @
 je transcedentalan broj, dokazuje se iz Lindeman-Vajerstrasove teoreme. Da nije transcedentalan, tj da je algebarski(sto znaci da postoji polinom sa racionalnim koeficijentima tako da je on nula tog polinoma), imamo da je i 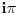 algebarski, onda iz Lindeman-Vajerstrasove teoreme sledi da je i 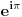 transcedentalan, a kako je vrednost ovog izraza -1, sto je algebarski broj, imamo kontradikciju.
Lindeman-Vajerstrasova teorema: Neka su 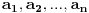 algebarski brojevi takvi da nijedan nije nula. Neka su 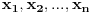 razliciti algebarski brojevi. Tada 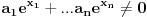
Pitanje: Ako je (M,d) kompletan metricki prostor i 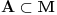 takav da se moze predstaviti kao prebrojiva unija nigde gustih skupova, onda je M\A gust u M. Tacno ili netacno?
P.S.(skup 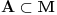 je nigde gust u M ako je unutrasnjost njegovog zatvorenja prazan skup.)
[Ovu poruku je menjao Milosh Milosavljevic1 dana 04.07.2013. u 17:54 GMT+1]
[Ovu poruku je menjao Milosh Milosavljevic1 dana 04.07.2013. u 17:55 GMT+1]
[Ovu poruku je menjao Milosh Milosavljevic1 dana 04.07.2013. u 17:55 GMT+1][ Sonec @ 04.07.2013. 15:38 ] @
Trebalo je da se pokaze da je  iracionalan, a ne transcendentan, al dobro.
Odgovor na tvoje pitanje je: tacno. Samo cu reci: Berova teorema o kategorijama. [ Milosh Milosavljevic1 @ 04.07.2013. 16:10 ] @
Da, ali znamo da trancsedentan => iracionalan (obrnuto ne vazi, primer je koren iz tri). Upravo sam shvatio da je ovo jedini dokaz iracionalnosti broja pi koji znam, moracu da pronadjem jos neke, mozda malo elementarnije dokaze  [ Sonec @ 04.07.2013. 16:19 ] @
Da, ali dokaz Lindemann–Weierstrass-ove teoreme nije bas naivan, tako da mi je to malo teska artiljerija.
Jedna od mogucnosti da se pokaze da je  iracionalan jeste da se prvo pokaze da je 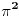 iracionalan. Nedeljko je jednom prilagao svoj PDF dokument o iracionalnosti (uopste), i tu se moze naci taj dokaz, kao i dokaz opste teoreme koja ce nam pomoci da iz iracionalnosti broja 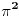 izvucemo iracionalnost broja  . [ number42 @ 04.07.2013. 17:15 ] @
trebo bi @sonec da postavi pitanje jer je tacno odgovorio, ali ako ne zeli moze neko drugi.... eto npr ja 
sesti zadatak:
postoje samo tri dvocifrena broja  , za koje je u izrazu 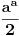 zadnja cifra 1.
tacno ili netacno? [ Sonec @ 04.07.2013. 17:34 ] @
Ne, ne moze taj zadatak. Sad sam ja na redu.
Pitanje: ova tema je debilozna? Tacno ili netacno?
[ number42 @ 04.07.2013. 17:59 ] @

@sonec,
odgovor: subjektivni osecaj. i sta postujes na temi ako ti se ne svidja :P
ajde matematicari, evo zadatak broj 6. siguran sam samo za jos jednog forumasa da moze da ga resi jer je vec diskutovao o tome, za ostale ne znam... [ darkosos @ 04.07.2013. 18:39 ] @
@Sonec
Tacno.
[ Milosh Milosavljevic1 @ 04.07.2013. 19:15 ] @
Ne slazem se sa pitanjem, pridev debilozna ne postoji. Pridev nastao od imenice debil je debilan/debilni/debilno/debilne. :D
[ number42 @ 04.07.2013. 19:21 ] @
e ajd zamolicu sve da se suzdrzimo od komentara koji nemaju veze s matematikom, i da ih ostavimo za neke druge teme ili pp, il sta vec.
hvala
[ number42 @ 04.07.2013. 19:25 ] @
evo da ponovim zadatak, ako se izgubio u offtopic komentima.
mozda je malo tezi, al eto ima 24 casa fore za resavanje.
postoje samo tri dvocifrena broja  , za koje je u izrazu 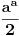 zadnja cifra  .
tacno ili netacno? [ Milosh Milosavljevic1 @ 04.07.2013. 19:40 ] @
Za ovaj sa a^a. Netacno, ne postoji ni jedan takav dvocifreni broj. a je sigurno paran broj, da bi a^a/2 bio ceo, ne zavrsava sa 0, jer bi stepenovan sam sa sobom dao 0 kao poslednju cifru, a ni jedan od izraza 2^2,4^4,6^6,8^8 ne daje kao poslednju cifru 2.
pitanje: U hiperbolickoj geometriji, svake dve prave u ravni imaju tacno jednu zajednicku normalu. Tacno ili netacno?
[ paparazzo @ 04.07.2013. 19:44 ] @
sjajna tema....momci(i devojke )svaka čast za temu,ja pojma nemam o matematici ali sam sa velikom pažnjom pročitao sve...i ako ništa ne razumem....nažalost...
[ number42 @ 04.07.2013. 20:07 ] @
@milosh milosavljevic1,
bravo, to je to.
mada, ciljao sam na opsti slucaj ali nisam znao kako da ga formulisem, jer 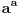 se nikada ne zavrsava dvojkom (barem sam ja tako dobio racunanjem), a to znaci da ni njegova polovina ne moze da se zavrsava cifrom 1.
Citat: Milosh Milosavljevic1:
pitanje: U hiperbolickoj geometriji, svake dve prave u ravni imaju tacno jednu zajednicku normalu. Tacno ili netacno?
mmm... nemam pojma 
bas me zanima odgovor. [ Nedeljko @ 04.07.2013. 20:17 ] @
Citat: Milosh Milosavljevic1: Za ovaj sa a^a. Netacno, ne postoji ni jedan takav dvocifreni broj. a je sigurno paran broj, da bi a^a/2 bio ceo, ne zavrsava sa 0, jer bi stepenovan sam sa sobom dao 0 kao poslednju cifru, a ni jedan od izraza 2^2,4^4,6^6,8^8 ne daje kao poslednju cifru 2.
pitanje: U hiperbolickoj geometriji, svake dve prave u ravni imaju tacno jednu zajednicku normalu. Tacno ili netacno?
Netačno za paralelne prave i prave koje se seku.
Sledeći zadatak: Zbir prvih milion cifara broja  u sistemu sa osnovom 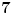 je: [ Nedeljko @ 04.07.2013. 20:19 ] @
E, da, da uradim zadatak o iracionalnosti broja 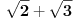 .
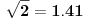 ,
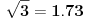 ,
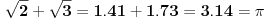 ,
pa pošto je  iracionalan broj, prema tome dabome. [ Nedeljko @ 04.07.2013. 20:21 ] @
[ Milosh Milosavljevic1 @ 04.07.2013. 20:36 ] @
Ako pretpostavimo ekvidistribuciju cifara u broju pi, njihov zbir je 1000000*9/2= 4500000, jos samo da se to prebaci u osnovu 7 xD xD
@Nedeljko Dokaz iracionalnosti 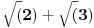 , neprocenjivo  [ number42 @ 04.07.2013. 20:42 ] @
Citat: paparazzo:
sjajna tema..
ma znam  ... hvala.
Citat: paparazzo:
..momci(i devojke )svaka čast za temu,ja pojma nemam o matematici ali sam sa velikom pažnjom pročitao sve...i ako ništa ne razumem....nažalost...
@paparazzo,
slobodno se ukljuci u temu sa bilo kojim zadatkom, a koji ce ti mozda biti razumljiviji.
mogu i laksi i tezi zadaci, svejedno.
[ Nedeljko @ 04.07.2013. 20:48 ] @
Citat: Milosh Milosavljevic1: Ako pretpostavimo ekvidistribuciju cifara u broju pi, njihov zbir je 1000000*9/2= 4500000, jos samo da se to prebaci u osnovu 7
Izračunaš nbroj pi u sistemu sa osnovom 7, pa sabereš prvih milion cifara. [ number42 @ 04.07.2013. 23:02 ] @
samo bih potsetio da se zadaci, po pravilima teme, postavljaju sa resenjem, i da li je tacno ili ne.
i u naslovu koji je broj pitanja da se ne bi zagubili u preklapanju zadataka.
[ number42 @ 04.07.2013. 23:05 ] @
svaki ceo pozitivan broj se uvek moze napisati kao odnos povrsine i obima nekog pravougaonika cije su stranice celi brojevi.
tacno ili netacno?
[ number42 @ 05.07.2013. 18:21 ] @
kako nema odgovora, da postavim resenje.
tacno je, bilo koji ceo pozitivan broj n se moze predstaviti kao kolicnik povrsine i obima nekog pravougaonika celih a i b.
stranice pravougaonika bi bile
a=2n+2
b=n(2n+2)
evo moze ko zeli sledeci, da postavi deveti zadatak, bilo koje tezine od najlaksih do najtezih.
[ zzzz @ 05.07.2013. 23:40 ] @
9-eto pitanje
N-to cifren prirodan broj kvadriramo.Rezultat ima posljednih N cifara jednakih početnom broju.Rješenja ima i to baš dva,
Točno netačno?
[ dusans @ 05.07.2013. 23:57 ] @
Netačno, ima ih bar 3 - 5, 25, 625.
Neka neko drugi postavi pitanje.
[Ovu poruku je menjao dusans dana 06.07.2013. u 01:08 GMT+1]
[ Nedeljko @ 06.07.2013. 01:02 ] @
Da li su prvih  decimala broja 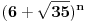 devetke?
[Ovu poruku je menjao Nedeljko dana 06.07.2013. u 02:14 GMT+1][ Nedeljko @ 06.07.2013. 11:29 ] @
Dokazuje se u dva reda, ali ocigledno da tema nikoga ne zanima.
[ number42 @ 06.07.2013. 13:18 ] @
za broj
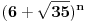
kada je n=16 onda ima 17 devetki kao pocetnih decimala, tj razlikuju se.
http://www.wolframalpha.com/in...%286%2B%5Csqrt%7B35%7D%29%5E16
[ number42 @ 06.07.2013. 13:26 ] @
evo nesto iz primenjene matematike.
kada je u 17. veku dekart pisao svoju studiju o sneznim pahuljicama, ispravno je utvrdio da njihov geometrijski oblik nije simetrican, a nije bio u pravu da su uvek sa 6 uglova (stranica, krakova..).
ono sto dekart nije znao je da se verovatnoca da, jedna za drugom, na zemlju, na isto mesto, padnu dve identicne pahuljice ne moze utvrditi.
tacno ili netacno?
[ number42 @ 06.07.2013. 13:59 ] @
zaboravio sam da ne mogu hipoteze 
pretpostavka je da ne postoje dva identicna geometrijska oblika sneznih pahuljica, pa se verovatnoca moze izracunati- verovatnoca da padnu dve iste je uvek nula.
moze neko drugi da postavi zadatak. [ Nedeljko @ 06.07.2013. 18:15 ] @
Razlisli još jednom o ovom tvom primeru. Šta su prvih 16 decamala tog broja? [ berazorica @ 06.07.2013. 21:52 ] @
uklještenje između 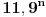 i 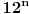 , pa kako u 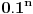 imamo jedinicu na n-tom mestu...? [ Nedeljko @ 06.07.2013. 22:25 ] @
Hajde, elaboriraj. Ne mogu ovako da odgovaram.
[ miki069 @ 06.07.2013. 23:01 ] @
Citat: berazorica:
uklještenje između 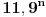 i 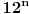 , pa kako u 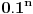 imamo jedinicu na n-tom mestu...?
Tačno je da je:
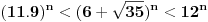
Kada bi pokazali da važi:
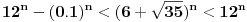
Onda bi bilo dokazano tvrđenje.
Nažalost je:
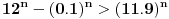
Tako da nam "ukleštenje" ne pomaže.
Treba uvestu sudiju da nebi svako proizvoljno tumačio tačnost/netačnost zadatka.
Neko već odvalio da pošto
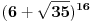 ima prvih 17 devetki iza decimalne tačke, ne stoji tačnost tvrđenja.
Tvrđenje je tačno.
[Ovu poruku je menjao miki069 dana 07.07.2013. u 00:30 GMT+1][ berazorica @ 06.07.2013. 23:42 ] @
^ da, videla sam da to nije to, ali ne mogu sad da razmišljam dalje, iako će da iscuri 24 sata
[ Nedeljko @ 07.07.2013. 01:06 ] @
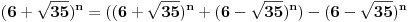 .
Umanjenik je prirodan broj jer se neparni stepeni broja 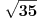 krate, a umanjilac je pozitivan broj manji od 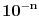 jer je
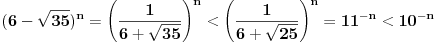 .
Stoga je 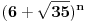 razlika prirodnog broja i pozitivnog broja manjeg od 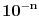 , pa su prvih  decimala devetke.
Tačan odgovor na pitanje prvih koliko decimala su devetke tako da posle ide cifra različita od devetke 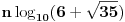 zaokrugleno na manji ceo broj. Na primer, za 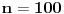 su prvih 107 decimala devetke, a 108-ma nije devetka. [ Nedeljko @ 07.07.2013. 01:44 ] @
Kod broja 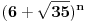 iza 107 devetki ide 756. Kako to odrediti?
Pa, treba odrediti umanjilac. On glasi 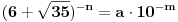 za neko realno 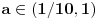 i neki prirodan broj  . Logaritmovanjem dobijamo
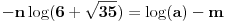 ,
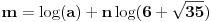 ,
gde je 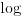 oznaka za dekadni logaritam. Obzirom da je 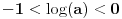 , zaključujemo da je  ništa drugo do najveći ceo broj koji je manji od 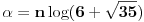 . Pritom je
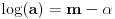 ,
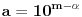 .
Stoga je za 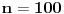
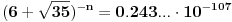 .
Zapravo, decimale broja 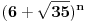 su iste kao decimale broja
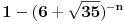 ,
a u ovom slučaju to je 107 devetki, pa 756... [ number42 @ 07.07.2013. 19:01 ] @
prosti brojevi koji su isti od pocetka ili od kraja su palindromski prosti brojevi, npr 797, ili 15 451.
od nule do dvadeset hiljada svi palindromski prosti brojevi imaju neparan broj cifara.
true or false?
[ dusans @ 07.07.2013. 19:33 ] @
True.
Svaki broj koji je palindrom i ima paran broj cifara je deljiv sa 11.
Tako da nema prostih palindroma među 4-cifrenim, 6-cifrenim, n2-cifrenim brojevima.
Neko drugi neka stavi pitanje.
[ number42 @ 07.07.2013. 20:00 ] @
you spell the word 'false' very strange 
broj 11 je palindromski prajm koji ima paran broj cifara.
jel mozes ukratko da postavis dokaz za ovo za nemogucnost palindromskog prajma sa parnim brojem cifara, hvala 
[ dusans @ 07.07.2013. 20:33 ] @
Hah, da u pravu si, na kraju sam prevideo 11.
Dokaz stvarno ne znam, primetio sam posmatrajući redove palindroma za parno-cifrene brojeve
da su uvek deljivi sa 11, tj. recept za dobijanje sledećeg plaindroma je dodati x*11 na trenutni ... npr:
1001 // Deljivo sa 11
1111 // +110
1221 // +110
1221 // +110
1331 // +110
....
1991 // +110
2002 // +11
2112 // +110
2222 // +110
...
100001 // Deljivo sa 11
101101 // + 1100
...
Zašto je to tako stvarno ne znam, a i da znam ne bih znao ovde da napišem i formulišem.
Očigledno da se radi o redovima i valjda bi se nekako dokazalo indukcijom, šta znam.
Evo ovde ima "nekakav" dokaz:
http://everything2.com/title/Palindromic+Prime
[ number42 @ 07.07.2013. 21:12 ] @
@dusans,
hvala na objasnjenju, zanimljivo razmisljanje.
ono na linku nisam bas skontao da li je dokaz ili pretpostavka, jer ako dobro prevodim, covek kaze:
"palindromski brojevi sa parnim brojem cifara su u obliku zbira brojeva ciji je izraz 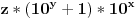 "
ali ne kapiram cime je to dokazao.
bilo kako bilo, moze neko da postavi sledeci zadatak.
[ Nedeljko @ 07.07.2013. 22:48 ] @
Neka prirodan broj  ima dekadni zapis  . To znači da je
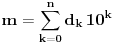 .
Po modulu 11 to izgleda ovako:
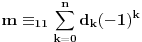
jer je 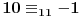 .
Stoga je
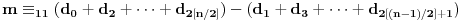 ,
gde je 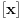 ceo deo od  .
Primera radi,
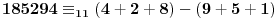 .
Drugim rečima, ako ciframa na parnom mestu nazovemo cifre uz stepen broja 10 na paran broj (cifre jedinica, stotina itd.), a ciframa na neparnom mestu cifre uz 10 na neparan broj (cifre desetica, hiljada itd.), onda razlika zbira cifara na parnim mestima i zbira cifara na neparnim mestima ima isti ostatak pri delenju sa 11 kao broj čiji je to zapis.
Odatle sledi da je broj deljiv sa 11 akko je pomenuta razlika deljiva sa 11. To je poznat kriterijum deljivosti sa 11. Konkretno, kod palindroma sa parnim brojem cifara ti zbirovi su jednaki, pa im je razlika 0, što je svakako deljivo sa 11.
Na sličan način se može formulisati kriterijum deljivosti sa 7.
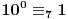 ,
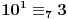 ,
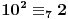 ,
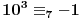 ,
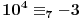 ,
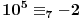 ,
Obzirom da je 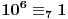 , za svako 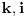 je 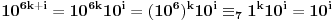 , tj. ovaj niz se periodično ponavlja, pa je
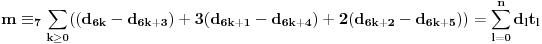 ,
gde je 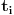 ostatak pri delenju 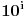 sa 7, što je periodičan niz sa periodom 6. [ Dexic @ 07.07.2013. 23:04 ] @
To se mnogo lakse moglo reci:
Ako je 4-cifren, onda je tipa abba, sto znaci da je jednak 1001a+110b, sto je 11*91a+11*10b, sto je 11*(91a+10b), sto je deljivo sa 11. I ovo je moglo mnogo prostije ;)
[ darkosos @ 08.07.2013. 07:44 ] @
Ma da, moze ovako: 11 je deljivo sa 11, dakle svaki broj-palindrom je deljiv sa 11...
@Nedeljko
Ovde je bila slicna tema (skoro pre 10 godina), i ostao je jedan neresen zadatak koji sam smislio tada, a cija postavka u potpunosti krsi tacku 6. Pravlinika :) Mislim da jeste zanimljivo, pa mozda mozemo da probamo da to sada dokrajcimo. [ number42 @ 08.07.2013. 08:38 ] @
Citat: dusans:
primetio sam posmatrajući redove palindroma za parno-cifrene brojeve
da su uvek deljivi sa 11
...
Zašto je to tako stvarno ne znam
ma evo jako je prosto. broj je deljiv sa 11 ako je razlika zbira cifara na neparnim mestima i parnim mestima deljiva sa 11, ili ako je jednaka nuli.
e bas ovo zadnje ne pise nigde, barem sam ja prvi put cuo za ovo i isprobao na par primera. potrazio sam na netu i bas nigde ne pise ovo pravilo o deljivosti s 11.
to bi bilo npr:
673552 => (6+3+5)-(7+5+2)=0 => deljivo s jedanaest 673552/11=61232
samim tim automatski vazi za palindrome sa parnim brojem cifara.
[ Nedeljko @ 08.07.2013. 10:24 ] @
Nula je deljiva svakim brojem, pa i brojem 11. Sve to piše u ovoj poruci:
http://www.elitesecurity.org/p3319320
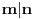 se u matematici definiše kao postojanje nekog celog broja  takvog da je 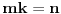 . Očigledno je 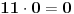 , pa 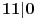 . [ Nedeljko @ 08.07.2013. 21:28 ] @
Citat: number42: e bas ovo zadnje ne pise nigde, barem sam ja prvi put cuo za ovo i isprobao na par primera. potrazio sam na netu i bas nigde ne pise ovo pravilo o deljivosti s 11.
Kakva laž! Da si pretražio ovu temu, našao bi. Takođe, na ovoj temi se nalazi link ka temi gde je dat opšti slučaj takvih kriterijuma deljivosti, koji se može primeniti na bilo koji delilac. [ number42 @ 08.07.2013. 21:54 ] @
i sad bi dosao 12. zadatak ako se ne varam.
ako neko zeli da postavi, moze. ako ne zeli, moze takodje  [ zzzz @ 09.07.2013. 01:04 ] @
Citat: zzzz:
9-eto pitanje
N-to cifren prirodan broj kvadriramo.Rezultat ima posljednih N cifara jednakih početnom broju.Rješenja ima i to baš dva,
Točno netačno?
Ovo nije rješeno.Malo ću pojasniti.Prirodan broj veći od jedan,ima n cifara u dekadskom sistemu.Kvadriramo ga i od toga oduzmemo taj broj.Rezultat ima toliko nula na kraju koliko je imao cifara početni broj.Ili ovako:Postoji neki prirodan broj zapisan u dekadskom sistemu koji kad se kvadrira daje rezultat takav da su njegove zadnje cifre identične početnom broju.
Uzmimo naprimjer 20-to cifren broj kiji ima takvu osobinu.
Postoje li dva takva dvadesetocifrena broja ili ne?Isto pitanje i za N-to cifrene brojeve.
(Ovo je Euklid znao riješiti,mada neki tvrde da ide i rekurzija pomoću matematičke indukcije što treba isprobati ) [ number42 @ 09.07.2013. 06:41 ] @
Citat: Postoji neki prirodan broj zapisan u dekadskom sistemu koji kad se kvadrira daje rezultat takav da su njegove zadnje cifre identične početnom broju.
Postoje li dva takva dvadesetocifrena broja ili ne?Isto pitanje i za N-to cifrene brojeve.
ne bih rekao.
ako proveravamo zadnju cifru od 0 do 9, uslov ispunjavaju samo 0, 1, 5, i 6.
onda idemo metodom ...xyz0^2, ...xyz1^2, ...xyz5^2 i ...xyz6^2.
i onda se resava klasicno mnozenjem olovkom na papiru.
odmah otpadaju nula i jedinica posle prve cifre i ostaju 5 i 6.
i odmah se vidi da (pocevsi od kraja) iz prve cifre nuzno sledi druga, iz druge treca, itd.
petica otpada posle trece cifre, a za sesticu postoji cetvorocifreni broj koji ispunjava uslove, 9376, a cifre nuzno proizilaze jedna iz druge.
za vise cifara nisam proveravao, tj da li se i taj niz prekida nakon neke cifre. ako nema prekida, pretpostavljam da je sablon periodicnog ponavljanja cifara.
ako je potrebno mogu i da napisem postupak, nije nesto komplikovano, nego me mrzi da petljam s latexom.
tako da bi trebalo da je to jedini cetvorocifreni broj koji ispunjava uslove ako nisam negde pogresio, pa je to onda, valjda, i dovoljan i potreban uslov za obaranje pretpostavke 
jel to to? [ miki069 @ 09.07.2013. 07:05 ] @
Za jednocifrene postoje dva:
5^2 = 25
6^2 = 36
6 + 5 = 11
Za dvocifrene postoje dva:
25^2 = 625
76^2 = 5.776
76 + 25 = 101
Za trocifrene postoje dva:
625^2 = 390.625
376^2 = 141.376
376 + 625 = 1.001
Za četvorocifrene postoji jedan:
9.376^2 = 87.909.376
10.001 - 9.376 = 625 što je trocifren broj.
[ Nedeljko @ 09.07.2013. 14:51 ] @
Ispitati da lipostoji prirodan broj koji ima osobinu da kada mu se poslednja cifra prebaci na prvo mesto, dobije se 6 puta veći broj.
[ number42 @ 09.07.2013. 17:00 ] @
ako poslednju cifru nekog broja premestimo na bilo koje mesto, ne dobijamo nikada sest puta veci broj, jer bi u suprotnom, ako je x taj broj a y zadnja cifra, bilo x=y(10^z-1)/59 a to je nemoguce.
[ number42 @ 09.07.2013. 17:03 ] @
n=Pt/Ot
svaki ceo pozitivan broj se moze napisati kao odnos povrsine i obima nekog trougla cije su stranice celi brojevi.
tacno il ne?
[ Nedeljko @ 09.07.2013. 18:42 ] @
Nažalost, rešenje ti nije tačno. Taj broj postoji i iznosi
1016949152542372881355932203389830508474576271186440677966
E, sad, kako doći do njega?
[ miki069 @ 09.07.2013. 22:16 ] @
Oznake: X je taj broj, n je broj cifara, Y poslednja cifra.
Po uslovima zadatka mora da važi:
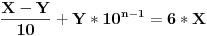
Odakle rešavanjem po X se dobija veza koju je već dao number42:
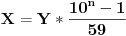
Traži se da 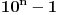 bude deljiv sa 59.
[ Nedeljko @ 09.07.2013. 22:42 ] @
To je to.
Može li sada neko da dokaže, da za svaku osnovu 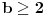 i za svaku ne-nula cifru  sistema sa sonovom  postoji broj koji kada se zapiše u sistemu sa osnovom  , premeštanjem poslednje cifre na prvo mesto se dobija  puta veći broj? [ darkosos @ 09.07.2013. 22:42 ] @
n=58 je resenje koje se dobija koristeci malu Fermaovu teoremu ( http://sh.wikipedia.org/wiki/Mala_Fermaova_teorema). A moze da se primeni zato sto je 59 prost broj. Pitanja koja bi zaokruzila ovu pricu su:
- da li ovakvih brojeva ima beskonacno mnogo?
- da li postoji resenje ako umnozak nije 6?
Ovo ne mora da se shvate kao zadaci za ovu "temu", vise bih voleo da se ovo uradi u posebnoj temi sa odgovarajucim naslovom. A ovde bih prepustio Nedeljku da da i sledeci jer su njegovi zadaci najinteresantniji. Ili jos bolje, ako ima takvih jos, da otvara posebne teme za njih. [ Nedeljko @ 09.07.2013. 22:44 ] @
Tako je Darko. Evo u mojoj prethodnoj poruci koju sam objavio dok si ti kucao poruku imaš sledeći zadatak.
[ darkosos @ 09.07.2013. 22:51 ] @
Primer je dobar da se pokaze da se ne moze uvek na prosta pitanja odgovarati elementarnom matematikom. Iako bi se do resenja moglo doci i programom, odgovor na pitanje da li postoji beskonacno mnogo takvih brojeva ne moze se dobiti bez to malo teorije... I da, zaboravih na jos jedno pitanje: da li su resenja koja se dobijaju Fermaovom teoremom sva resenja?
[ zzzz @ 10.07.2013. 07:55 ] @
Izračunati ovaj broj nije teško čak niti ovako ručno.Jednostavno treba pomnožiti neki broj sa 59 da se dobije broj sa sve samim devetkama.Pa onda krenemo odzada i odmah vidimo grešku.Fali 1 kao zadnja cifra.
10169491525423728813559322033898305084745762711864406779661
1*59=59,imamo tu poslednju devetku.Zatim zbog prenosa 5 trebamo množenjem dobiti 4,a to je 6*59=354.Predzadnji broj je 6.Prenos 35 odbijamo od devetki pa opet.... i tako sve dok nam prenos ne bude 99.
Prilično to sa prenosima liči na haotično smjenjivanje,sa intuitivnim osjećajem da se kad tad trebaju pojaviti devetke.I da će se to sve periodično ponavljati.Dakle možemo odmah napisati sledeći veći broj koji pomnožen sa 59 daje sve same devetke.Ako bi se periodičnost uočila,a devetke nisu izašle,djeljivosti nema.
Ujedno to je možda način rješavanja sledećeg zadatka.
[ darkosos @ 10.07.2013. 09:15 ] @
To jeste trazeni broj, nego je potrebno jos pomnoziti sa poslednjom cifrom (Y=6) da bi se dobio X (koristim oznake iz poruke koju je napisao miki069). Dakle Milane, kada dobijes rucno taj broj (koji se zavrsava sa 1), onda jos treba da ga pomnozis sa 6 i dobices broj koji je Nedeljko napisao kao resenje (proverio sam racun koristeci wolfram).
[ Nedeljko @ 10.07.2013. 10:22 ] @
Ne, neće se Fermaovom teoremom dobiti sva rešenja. Vidi Karmajkelovu funkciju na primer.
Dakle, može li neko da dokaže da za svaku osnovu i svaku nenula cifru te osnove postoji rešenje? [ Nedeljko @ 10.07.2013. 13:57 ] @
Evo jednog programa koji ispisuje taj broj. Poenta u odnosu na priču člana zzzz je da se izbegne naknadno množenje sa 6 tako što će se sa 59 deliti broj 5999...9994.
Code (c):
#include <stdio.h>
int main ()
{
int n = 59;
while (1) {
int c = n /59;
printf("%d", c );
n -= 59*c ;
if (n == 5) {
printf("\n");
break;
}
n *= 10;
n += 9;
}
return 0;
}
[ number42 @ 10.07.2013. 16:28 ] @
odgovor na 13. zadatak
Citat:
n=Pt/Ot
svaki ceo pozitivan broj se moze napisati kao odnos povrsine i obima nekog trougla cije su stranice celi brojevi.
tacno il ne?
tacno.
stranice tog trougla, ako nisam nesto pogresno prepisao iz ovih mojih zvrljotina iz sveske, bi trebalo da budu
a=n+2
b=n(n+1)/2
c=n(n+1)
[ Nedeljko @ 10.07.2013. 17:05 ] @
Zadatak je postavljen ovde
http://www.elitesecurity.org/p3320067
Ima oko četiri ipo sata do objavljivanja rešenja. Tvoj zadatak možda niko nije rešavao zato što si ga postavio, a da prethodni nisi rešio. Ponudio si netačan odgovor.
Uostalom, ni rešenje ovog ti nije tačno, jer na primer za n=3 dobijaš da su stranice a=5, b=15 i c=30, koje ne odgovaraju nijednom trouglu jer nije a+b>c. [ Nedeljko @ 10.07.2013. 17:26 ] @
Inače, jedno od tačnih rešenja tog zadatka je
a=5n,
b=12n,
c=13n.
[ number42 @ 10.07.2013. 17:40 ] @
eto ko hoce da postavi 14. zadatak.
a mogli bi i nesto lakse, da se ukljuci veci broj ljudi, da se dobiju dodatne perspektive posmatranja zadataka, i sl.
[ darkosos @ 10.07.2013. 21:35 ] @
Citat: Nedeljko:
Može li sada neko da dokaže, da za svaku osnovu 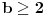 i za svaku ne-nula cifru  sistema sa sonovom  postoji broj koji kada se zapiše u sistemu sa osnovom  , premeštanjem poslednje cifre na prvo mesto se dobija  puta veći broj?
Na isti nacin kako je miki069 prikazao za slucaj 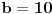 , a istu formulu napisao i number42, moze se dobiti da je trazeni broj jednak 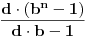 . Dovoljno je pokazati da uvek postoji n takvo da je 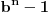 deljivo sa 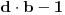 , iako bi naravno moglo da se desi i da  ima zajednicki faktor sa imeniocem. Samo da napomenem da ako se dozvoli da je 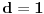 zadatak je trivijalan (resenje je uvek 11, a ako se dozvoli jednocifren broj, onda i 1).
Naravno, uslov ce biti ispunjen ako je 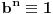 po modulu 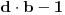 . U opstem slucaju nije prost broj 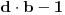 pa umesto Fermaove teoreme, mozemo da koristimo Ojlerovu. Treba samo pokazati da je 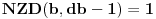 ali to je jednako 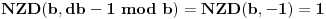 .
Dakle, to su uvek uzajamno prosti brojevi, pa se primenom Ojlerove teoreme nalazi da je 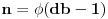 gde je 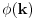 Ojlerova funkcija Ojlerova funkcija koja predstavlja broj uzajamno prostih brojeva sa k, koji su manji od k. U slucaju da je bd-1 prost broj, kao u prvoj postavci ovog zadatka, 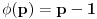 jer su svi brojevi manji od prostog broja p uzajamno prosti za njim. [ number42 @ 10.07.2013. 21:52 ] @
kvadrat plus jedan nikada nije stepen.
( 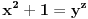 je nemoguce, kada su 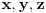 celi brojevi veci od jedan)
tacno ili netacno? [ darkosos @ 10.07.2013. 22:02 ] @
Verovatno si hteo da stavis jos neke uslove, obzirom da je 1^2 + 1 = 2^1, kao i da je y=x^2 + 1, z=1 uvek resenje...
Sada vidim da si promenio postavku... Samo mi nije jasno kako uvek sebe samoproglasis nastavljacem? :)
EDIT: dosadan je :)
[Ovu poruku je menjao darkosos dana 11.07.2013. u 08:34 GMT+1]
[ number42 @ 10.07.2013. 22:06 ] @
evo izmenio sam, za vece od jedan.
EDIT: fokusiraj se na zadatak  [ Nedeljko @ 11.07.2013. 09:01 ] @
Jeste Darko, to je rešenje.
number42
Zar nisi pomislio da je Darko ovo rekao zato što je prethodno izrazio želju da ja postavim zadatak i da ne želi da se koncentriše na tvoj?
Evo ga za one koji žele moj zadatak:
Neka je  pozitivan realan broj i neka je na skupu 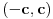 definisana binarna operacija  na sledeći način:
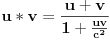 .
Ovo je ono što mnogi pogrešno zovu "relativističko sabiranje brzina", što svakako nije sabiranje, jer za sabiranje važi 1+1=2. Takođe, u STR je primenljivo samo na kolinearne brzine (jednodimenzion slučaj).
Ovo obrazuje komutativnu grupu. Ispitati da li je ona izomorfna grupi 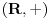 , odnosno da li postoji bijektivno preslikavanje 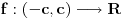 takvo da je 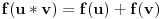 . Drugim rečima, možemo li svakoj brzini pridružiti neku realnu karakteristiku koja tu brzinu potpuno određuje, tako da se pri slaganju brzina te karakteristike sabiraju? Ako postoji, navesti tu funkciju  , tj. karakteristiku koja se sabira. [ number42 @ 11.07.2013. 18:45 ] @
Citat:
kvadrat plus jedan nikada nije stepen.
( 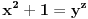 je nemoguce, kada su 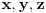 celi brojevi veci od jedan)
tacno ili netacno?
odgovor za 15. zadatak: tacno je.
ako je z parno, onda imamo
x^2+1=(y^k)^2
kako je najmanja razlika kvadrata 3, onda je 1 nemoguce i ovo je netacno.
ako je z neparno onda mozemo napisati dve jednacine
c^2+1=y^(2k+1)
d^2+1=y^(2k-1)
podelimo jednu s drugom, i dobijamo
(c^2+1)/(d^2+1)=y^2
pretpostavimo da je ovo tacno i da se leva strana moze zapisati kao kvadrat. onda ona mora da ima oblik
(a^(n+2m)) / (a^n) = (a^(1+m))^2 / a^2 = (c^2+1)/(d^2+1)
kako kvadrat ne moze biti jednak kvadrat plus jedan, onda je netacno i za neparno z iz postavke.
dakle, kvadrat plus jedan nije nikada stepen.
[ Nedeljko @ 11.07.2013. 19:48 ] @
Citat: number42: ako je z neparno onda mozemo napisati dve jednacine
c^2+1=y^(2k+1)
d^2+1=y^(2k-1)
Hahaha! Ovo si samo ti mogao da lupiš. Možemo mi napisati i sto jednačina, ali ove dve jednačine zajedno nemaju nikakve veze sa zadatkom. Postavka se može napisati na bilo koji od dva navedena načina, ali za različite vrednosti za k koje odgovaraju istoj vrednosti za z.
Inače, tvrđenje zadatka je tačno i specijalan je slučaj Katalanove hipoteze koja je dokazana 2002 godine.
Naravno, to ne govori ništa o "ispravnosti" rešenja koje je ponudio number42. Nisam ni mislio da on zna da reši ova dva zadatka, ali me je baš zanimalo šta će da lupi. [ number42 @ 11.07.2013. 20:18 ] @
moze sledeci
[ darkosos @ 11.07.2013. 21:39 ] @
@Nedeljko
Stvarno mislim da bi trebalo da otvaras novu temu ako imas neki interesantan zadatak. Meni licno ne odgovara ovaj format. Pored toga, ubacuju se preko reda a kvalitet izlozenog se srozava, da ne govorim o "dokazima". Ne mozemo da se dogovorimo ni ko je sledeci. Neka ova tema ostane ono sto jeste.
[ miki069 @ 11.07.2013. 21:48 ] @
Nula je neutralni element prve grupe i neutralni element druge grupe, pa mora da važi: 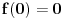
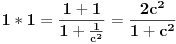
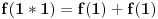
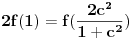
Slično se dobija da važi:
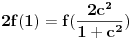
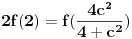
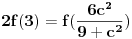
.
.
.
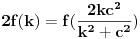
Samo još nedostaje "sitnica". Šta je f(x)?
Lupno sam da je: 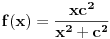 ,
ali mislim da ne prolazi definiciju morfizma: 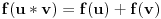 ili ja ne znam da proverim.
[Ovu poruku je menjao miki069 dana 11.07.2013. u 23:01 GMT+1]
[Ovu poruku je menjao miki069 dana 11.07.2013. u 23:03 GMT+1][ number42 @ 11.07.2013. 22:28 ] @
samo jedan offtopic.
kao pokretac teme, zamolio bih, jos jednom, da koristimo korektnu komunikaciju na ovoj temi.
sve koji ne zele da ispostuju ovo, zamolicu da otvore druge teme gde ce komentarisati kako zele i koje ce koncipirati po vlastitoj volji.
takodje i one koji pishu da im se ova tema ne svidja a onda komentarisu na istoj, usmerio bih ka drugim, njima zanimljivijim temama, ili otvaranje novih.
hvala unapred
[ number42 @ 11.07.2013. 22:33 ] @
@miki069,
ne znam da li si resio? ako jesi, sada bi isao 17. zadatak, valjda (ili kad bude reseno).
a i ti bi mogao da postavis nesto, m? 
il vec ko zeli.. [ Nedeljko @ 12.07.2013. 09:34 ] @
number42
Da, da, treba da ignorišemo gluposti koje pišeš. To si mi odavno napisao u PP - da ne želiš da se ukazuje na tvoje greške. To je vrlo nekorektno od drugih. E, pa vidiš, ako si to hteo, onda toj temi uopšte nije mesto na ovom forumu, jer je ovo forum za matematiku. U tom slučaju si temu trebao da pokreneš na Ultra MadZone, koji je izgleda ukinut.
Je li Bojane, koji je forum namenjen ovome što number42 hoće? Ima li takvoga nečega na sajtovima elitesecurity i elitemadzone?
[ Nedeljko @ 12.07.2013. 09:37 ] @
Citat: miki069: mislim da ne prolazi definiciju morfizma: 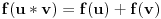 ili ja ne znam da proverim.
Ne prolazi. [ Nedeljko @ 12.07.2013. 11:07 ] @
Oddgovor je funkcija 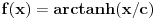 , ali ću naknadno napisati kako se dolazi do nje. [ Nedeljko @ 12.07.2013. 12:56 ] @
Evo, istekao je jedan dan, pa da objavim rešenje zadatka.
Neka je 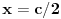 i utvrdimo šta je 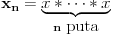 .
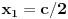 ,
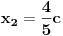 ,
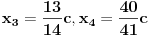 ,
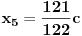 .
Izgleda da je 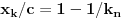 za neki niz prirodnih brojeva 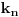 . U svakom slučaju, broj 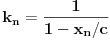 postoji, pa bio prirodan ili ne. Odredimo rekurentne formule.
 ,
pa je
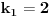 ,
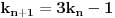 .
Podelimo poslednju jednačinu sa 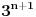 .
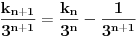 .
Za niz 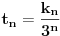 važi
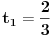 ,
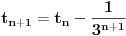 .
Odavde je lako zaključiti da je
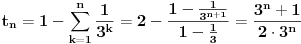 .
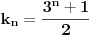 ,
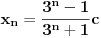 .
Dakle, 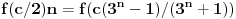 , odnosno
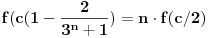 .
Neka je 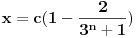 ,
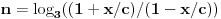 ,
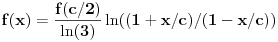 .
Naravno, ova jednakost je izvedena samo za neke realne brojeve  . Probajmo sa funkcijom definisanom sa
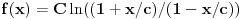 , 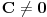 .
za sve 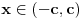 .
Neposredno se proverava da ona zaista zadovoljava traženi uslov
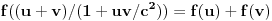 .
No, to je tačno arkus tangens hiperbolički od 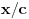 pomnožen konstantom 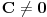 . [ number42 @ 12.07.2013. 16:34 ] @
ovo je stoti komentar na ovoj temi. hteo bih malu statistiku do sada:
za ovih 10 dana trajanja teme, do sada je bilo:
-100 komentara
-6100 pregleda,
-16 obradjenih zadataka od najlaksih do najtezih,
-13 ljudi je ucestovalo u resavanju zadataka
i, malo sam uporedjivao sa ostalim temama, i ovo je najuspesnija tema na pdf matematika za ovaj vremeneski period, ikada, a da nije bilo opstrukcija celim trajanjem teme- bila bi jos uspesnija.
hvala svima koji su se potrudili i svojim doprinosom omogucili ovako sjajan rezultat 
za svega 10 dana.
za mene licno, ovakav oblik teme mi bas odgovara, jer za 10 dana nikada u zivotu nisam naucio toliko novih stvari iz matematike ili usavrsio koje vec znam, sa mozda maksimum 2 sata dnevno zvrljanja ili kuckanja, i to ono amaterski, kao hobi.
jos jednom hvala svima koji su dobronamerno ucestovali na temi i gde smo svi zajedno omogucili da, do sada, bude najuspesnija na pdf matematika. [ number42 @ 12.07.2013. 16:37 ] @
evo nesto lagano da se ukljuci veci broj ljudi:
"jednaipo trecina od dveipo sestine od 24 je 17"
tacno ili netacno?
[ number42 @ 13.07.2013. 18:16 ] @
odgovor na 17. pitanje je pet. dakle netacno.
ako neko zeli da postavi neki zanimljiv zadatak, moglo bi.
[ zzzz @ 15.07.2013. 00:48 ] @
Najprije da riješim nešto pa da steknem prava postavljanja novog zadatka:
odgovor na 17. pitanje je pet. dakle netacno.
A sad prije postavljanja 18-naestog zadatka prepričaću šta sam nedavno negdje pročitao o kreativnosti.Navodno su neki ,negdje, uočili da školstvo izbacuje mnogo obrazovanih ljudi,ali da oni i pored savršenog znanja stečenog obrazovanjem nisu sposobni ništa novo kreirati.Neki novi programi u obrazovanju pokušavaju tome doskočiti .Naprimjer,postave učenicima nerješiv zadatak sa nedovoljno informacija,pa onda gledaju kako je ko pokušao da tome doskoči.Taj trud je mjerilo za ocjenjivanje kreativnih sposobnosti.
Ali ja ću u osamnaestom zadatku tvrditi nešto interesantno u vezi nedostatka informacija-viška informacija.
[ zzzz @ 15.07.2013. 00:50 ] @
18-ti zadatak:
Imamo logički problem koji je rješiv na jedinstven način.Dodamo li tom problem u osnovnu postavku dodatnu informaciju koja je savršeno istinita,taj problem nije rješiv.
Ili ovako:Grupa ljudi koja nezna tu istinitu informaciju će riješiti problem,a grupa ljudi koji znaju tu informaciju neće.
Tačno ?(navesti bar neki primjer).
Netačno?(dokazati nekom logičkom pričom).
[ number42 @ 15.07.2013. 16:02 ] @
evo da pokusam.
ne znam odgovor na ovaj zadatak, ama bas blage predstave.
znaci- potrebno je manje informacija da bih ga znao.
cista logika  [ igorpet @ 15.07.2013. 22:15 ] @
Nista nisam resio ali postavicu jedan, po meni primereniji, zanimljiv "problem":
Da li je broj 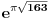 ceo?
Tacno ili netacno [ number42 @ 16.07.2013. 07:43 ] @
@zzzz,
ajd mozes i naknadno postaviti odgovor.
Citat: igorpet:
broj 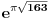 ceo
Tacno ili netacno
netacno, nije ceo broj.
to je hipoteza koju je postavio ramanudzan i koja je kasnije dokazana kao netacna. [ number42 @ 16.07.2013. 07:50 ] @
svaki prost broj od 5 do 101 se nalazi tacno u sredini izmedju neka dva prosta broja.
netacno, tacno?
[ number42 @ 16.07.2013. 18:08 ] @
izvinjavam se jer nisam sacekao da proteknu 24 casa, nisam siguran da cu tada biti u mogucnosti da odgovorim.
za 20. zadatak- tacno.
svodi se ustvari na specijalan slucaj goldbahove hipoteze, proverljive do 100 (svaki paran broj se moze napisati kao zbir dva prosta).
2Pb1=Pb2+Pb3
Pb1=(Pb2+Pb3)/2
next
[ zzzz @ 22.07.2013. 00:52 ] @
Citat: zzzz:
18-ti zadatak:
Imamo logički problem koji je rješiv na jedinstven način.Dodamo li tom problemu u osnovnu postavku dodatnu informaciju koja je savršeno istinita,taj problem nije rješiv.
Ili ovako:Grupa ljudi koja nezna tu istinitu informaciju će riješiti problem,a grupa ljudi koji znaju tu informaciju neće.
Tačno ?(navesti bar neki primjer).
Netačno?(dokazati nekom logičkom pričom).
Ovaj interesantan zadatak niko nije ozbiljno shvatio.Djeluje kontradiktorno!
Hoćete li da probamo uz moju malu pomoć?
[ number42 @ 22.07.2013. 18:02 ] @
naravno, samo shibaj. ne verujem da neko moze da reshi bez dodatnih informacija.
[ zzzz @ 24.07.2013. 18:42 ] @
Primjer za rješenje 18-tog.
Zadatak, http://www.elitesecurity.org/p193582 uspješno je rješavan na ovom forumu.Nećemo ga ponovo rješavati već samo da se podsjetimo.Neki zagonetač zadao je jednom logičaru sumu dva prirodna broja ne veća od 200,a drugom proizvod tih brojeva. S je izjavio da nezna koji su to brojevi,ali da zna i da P nezna .Na to je P uzvratio da on sada zna.Poslije nešto razmišljanja i S je rekao da i on zna.Rješenje ovog problema je bilo S=17 I P=52,a brojevi su 4 I 13.
Ovaj zagonetač zadao je taj isti zadatak novom paru logičara.Da bi im olakšao posao naveo je da umjesto 200,brojevi nisu veći od 30.Zatim je jednom šapnuo S=17,a drugom P=52…..(očito je da su obadva primjetila da su brojevi manji od 30,tj informacija je istinita.)
P je rekao da nezna (video je da su to možda 2 i 26 ili 4 i 13).S je rekao da nezna,ali da je već znao da ni P nezna.Iz ove izjave P je zaključio da se suma ne može prikazati kao zbir dva prosta broja,dakle nije parna. (Ali niti je neparna tako da se može napisati kao prost broj +2.)Zato je odmah odbacio par 2,26 i našao rješenje.
S je počeo da razmišlja.Ako 17 rastavim na sve moguće načine,mogu dobiti sledeće proizvode:30,42,52,60,66,70,72.Svaki od njih ću rastaviti na dva faktora na sve moguće načine,a zatim odbaciti sve one parove kao što je to uradio P.U onom što preostane potražiću rješenje.
Nije mogao naći rješenje.Omela ga je ona istinita informacija.
Ko zna objasniti?
[ Nedeljko @ 24.07.2013. 18:53 ] @
Znam ja.
[ miki069 @ 26.07.2013. 11:14 ] @
...Mogu dobiti sledeće proizvode:30,42,52,60,66,70,72....
Te mogućnosti je imao i kada je imao da su brojevii manji od 200.
Šta bi ga omelo sad kada zna da su manji od 30?
[ Nedeljko @ 26.07.2013. 13:16 ] @
Uspeo sam greškom da obrišem svoju prethodnu poruku, ali nije važno, jer je prvo bilo grešaka, a potom kada su ispravljene, objašnjenje nije bilo jasno.
Ovde imamo četiri agenta. Jedan je Z koji je zamislio brojeve, P i S su osobe kojima je saopštio proizvod, odnosno zbir tim redom i R je rešavač zadatka.
Recimo da imamo dva skupa informacija A i B, s tim da je skup B informativniji.
Informacija da nešto ne može da se zaključi na osnovu informacija A ne znači da to ne može da se zaključi na osnovu informacija B.
Rešavač ima informaciju o tome šta su P i S mogli da zaključe do tog trenutka, a šta nisu. Stoga proverava sve parove koji se uklapaju u ceo tok razgovora i istale činjenice. Kada se parametar 200 promeni na 30, onda se mogu desiti sledeće situacije:
1. Za par (4,13) usled dodatnih informacija postaje netačno da neko nešto nije znao na osnovu do tada dostupnih informacija.
2. Za neki drugi par usled dodatnih informacija postaje netačno da netačno da neko nešto nije znao od na osnovu do tada dostupnih informacija.
Prvi slučaj ne nastupa. Drugi slučaj može da znači da neki drugi par koji sa parametrom 200 nije mogao da zadovolji tok razgovora sa parametrom 30 može. Stoga se pored para (4,13) u skupu mogućih rešenja može pojaviti još nešto, pa rešavač ne može da se opredeli između više mogućih rešenja.
[ Nedeljko @ 26.07.2013. 18:58 ] @
Ako je granica manja od 13, rešenja nema.
Ako je granica od 13 do 60, onda je 4,13 jedinstveno rešenje.
Ako je granica od 61 do 200, onda osim rešenja 4,13 imamo i rešenje 4,61.
Prilažem izvorni kod programa za rešavanje zadatka na jeziku C++.
[ zzzz @ 27.07.2013. 00:16 ] @
Citat: miki069:
...Mogu dobiti sledeće proizvode:30,42,52,60,66,70,72....
Te mogućnosti je imao i kada je imao da su brojevii manji od 200.
Šta bi ga omelo sad kada zna da su manji od 30?
Miki,pitanje ti je sasvim dobro.Rastavi one proizvode na sve moguće načine.
Odbaci i one parove koji imaju bar jedan faktor veći od 30....Probaj,
[ Nedeljko @ 27.07.2013. 09:13 ] @
Onaj program vrši samo rastavljanja u datom opsegu. Dakle, radi grubom silom, po definiciji da ispravnost programa ne bi bila upitna.
Primer ti ne valja iz više razloga.
1. Odgovor na pitanje iz 18-tog zadatka je ne.
2. U ovakvim zadacima dodavanje tačnih informacija može informaciju iz zadatka (da neka uloga u nekom trenutku nije mogla da zna nešto) može iz tačne da pretvori u netačnu. Tu dodatnu informaciju sme da ima samo rešavač, a ne i uloge iz zadatka.
3. U konkretnom slučaju, kada je opseg 2,...,200, postoji više od jednog rešenja (primera radi, 4,13 i 4,61), a kada je opseg 30, postoji tačno jedno rešenje - 4,13.
[ Nedeljko @ 27.07.2013. 10:09 ] @
Samo da se ispravim.
Našao sam grešku u svom programu. Pri rastavljanju nije proveravao da li je i drugi činilac u opsegu. Popravio sam to i učinio program čitljivijim. Dakle, razlog 3 iz moje prethodne poruke otpada.
Zapravo, stvari stoje ovako:
Ako je gornja granica manja od 62, nema rešenja.
Ako je gornja granica u opsegu 62,...,200, onda jedinstveno rešenje postoji i ono je 4,13.
[ Nedeljko @ 27.07.2013. 11:29 ] @
Evo šta se dešava u slučaju da su zamišljeni brojevi 4 i 13 i da je gospodi saopštena granica 30.
Proizvod razmišlja: Mogućnosti su 2,26 i 4,13. Dakle, ne znam koji su to brojevi.
Suma razmišlja: Mogućnosti su 2,15, 3,14, 4,13, 5,12, 6,11, 7,10, 8,9, pa ne znam koji su to brojevi. U slučaju svake od njih se proizvod brojeva može u datom opsegu rastaviti na bar dva načina. Recimo, 5,6, 6,7, 2,26, 6,10, 3,22, 5,14, 4,18 u redosledu navedenih mogućnosti. Proizvod ne može da zna brojeve.
Proizvod kaže: Ne znam koji su to brojevi.
Suma kaže: Ne znam ni ja, ali sam znao da ni ti ne znaš.
Proizvod razmišlja: Ako su brojevi 2,26, onda je zbir 28. Broj 28 se može napisati kao 5+23. U tom slučaju Suma ne bi znao da ja nisam znao brojeve. Dakle, ta mogućnost otpada, pa ostaje samo 4,13.
Proizvod kaže: Ja sada znam koji su to brojevi.
Suma razmišlja: Ako su zamišljeni brojevi 2,15, onda se proizvod kolebao između 2,15, 3,10 i 5,6. Pretpostavku 2,15 ne bi uspeo da odbaci jer je faktički tačna. Proizvod bi pod njegovom pretpostavkom 3,10 za mene mislio da se kolebam između mogućnosti 2,11, 3,10, 4,9, 5,8, 6,7. Obzirom da 2,11 znači da je on mogao da zna koji su to brojevi, to bi mu se ne bi uklopilo u moj odgovor, pa bi tu pretpostavku mogao da odbaci. Takođe, on bi pod njegovom pretpostavkom 5,6 za mene mislio da se kolebam između mogućnosti 2,9, 3,8, 4,7, 5,6. Obzirom da svaka od tih mogućnosti znači da on nije mogao da zna koji su to brojevi, to bi mu se ne bi uklopilo u moj odgovor, pa bi tu pretpostavku mogao da odbaci. Stoga, on ne bi mogao da zna da li su brojevi 2,15 ili 5,6. Dakle, mogućnost 2,15 otpada.
Ako su zamišljeni brojevi 3,14, onda se proizvod kolebao između 2,21, 3,14 i 6,7. Pretpostavku 3,14 ne bi uspeo da odbaci jer je faktički tačna. Pretpostavku 2,21 bi lako odbacio jer je 2+21=4+19, pa ja ne bih na početku mogao da znam da on ne zna koji su to brojevi jer se 4*19 faktoriše na jedinstven način u opsegu od 2 do 30. Proizvod bi pretpostavku 6,7 odbacio na sličan način jer je 6+7=2+11, pa bi posle moje izjave mogao da zna koji su to brojevi. Stoga se mogućnost 3,14 ne može odbaciti.
Rešavač razmišlja: Suma ne može da eliminiše faktički tačnu mogućnost 4,13. Dakle, Suma na kraju neće moći da zna koji su to brojevi, odnosno 4,13 nije rešenje.
Zaključak: Spuštanje opsega sa 200 na 30 u slučaju 4,13 menja tačnost sledećeg iskaza iz tačno u netačno: U poslenjem koraku Suma nije znao da Proizvod na početku nije znao da je Suma na početku znao da Proizvod na početku nije znao brojeve. Da bi se to bolje razumelo, treba koristiti činjenicu da se znanje ne menja saznavanjem od ranije poznatih informacija. Ako neko nešto nije znao, pa je saznao, to znači da je u međuvremenu primio informaciju o nečemu što do tada nije znao.
[ zzzz @ 28.07.2013. 10:42 ] @
Odgovor na 18-to pitanje:DA,dodatna istinita informacija od rješivog zadatka pravi nerješiv .
Suma je analizirajući proizvode našao da 52,60 i 66 mogu dati rješenje.
--
52=2*26...(S=28);4*13...(S=17)-------rješenje je 4,13
66=2*33...(S=35);3*22...(S=25);6*11...(S=17)--------rješenje je 6,11
70=2*35...(S=37);5*14...(S=19);7*10...(S=17)-------rješenje je 7,10
Dakle dodatna istinita informacija je spriječila gospodina Sumu da otkrije brojeve 4,13.Da te informacije nije bilo,Suma zna da gospodin Proizvod nebi odbacio parove 2,33 i 2,35 pa bi mu preostalo samo jedno rješenje.(crveno su označene sume koje mogu da se rastave u dva prosta sabirka,kao i faktori koji su veći od 30.)
[ Nedeljko @ 28.07.2013. 13:58 ] @
Ako si mislio na to da Suma sa dodatnim informacijama ne može da sazna odgovor (a ne Rešavač), opet si se grdno prevario.
Ako je na početku opšte poznat skup informacija I, onda
1. Proizvod na osnovu I ne može da zna brojeve.
2. Suma na osnovu I ne može da zna brojeve, ali može da zna da Proizvod ne može da zna brojeve.
3. Proizvod na osnovu I i činjenica iz tačke 2 može da sazna brojeve.
4. Suma na osnovu I i činjenica iz tačke 3 može da sazna odgovor.
Kada se skup informacija I proširi do šireg skupa informacija J, onda
1'. Proizvod na osnovu J ne može da zna brojeve.
2'. Suma na osnovu J ne može da zna brojeve, ali može da zna da Proizvod ne može da zna brojeve.
3'. Proizvod na osnovu J i činjenica iz tačke 2' može da sazna odgovor.
4'. Suma na osnovu J i činjenica iz tačke 3' ne može da sazna odgovor.
Šta se desilo?
Iskaz 1' je jači od 1 jer je lakše nešto zaključiti iz više informacija, nego iz manje.
Iz istog razloga je prvi deo iskaza 2' jači od prvog dela iskaza 2, ali za drugi deo iskaza 2' ne možemo reći ni da je jači, ni da je slabiji od drugog dela iskaza 2, jer se iz više informacija (J umesto I) izvlači jači zaključlak (1' umesto 1). Stoga za iskaz 2' ne možemo reći ni da je jači, ni da je slabiji od iskaza 2.
Iskaz 3' nije ni jači ni slabiji od iskaza 3, jer se isti zaključak izvodi iz drugog skupa informacija koji nije ni širi ni uži, već postoje neke dodatne informacije nego u 3, ali su neke informacije takođe izgubljene.
Znanje da Pera na osnovu njegovog (meni nepoznatog) znanja i informacija I ne može da zaključi nešto mi je manje informacija nego da ne može da zaključi na osnovu njegovog znanja i J, ali mi je znanje da Pera može nešto da zaključi iz njegovog znanja i informacija I mi je više informacija nego da Pera na osnovu svog znanja i informacija J može to da zaključi.
E, tako u 4' Suma ne raspolaže svim informacijama kojima raspolaže u 4.
Evo prostijeg primera. Zamislio sam brojeve 3 i 8 i rekao im da su u opsegu 2,...,14.
Proizvod: Ne znam koji su to brojevi.
Suma: Ne znam ni ja, ali sam znao da ni ti ne znaš.
Zamislimo sada da je opseg bio 2,...,13. Suma bi na osnovu zbira 11 znao da je jedna od mogućnosti 4,7, kada bi Proizvod znao brojeve. Dakle, razgovor bi tekao ovako:
Proizvod: Ne znam koji su to brojevi.
Suma: Ne znam ni ja, a nisam znao da ni ti ne znaš.
To što Proizvod nešto ne može da zna na osnovu manje informacija, ne znači da ne može da zna na osnovu više informacija, pa Suma ne može da izvuče zaključak o Proizvodovom neznanju kada Proizvod poseduje više informacija, kao kada je mogao da izvuče zaključak o Proizvodovom neznanju kada je Proizvod imao manje informacija.
[ Nedeljko @ 28.07.2013. 14:01 ] @
Daj Sumi u prvom slučaju u poslednjem koraku informaciju koju je imao u prvom sliučaju u poslenjem koraku, tj. da bi razgovor sa parametrom 200 do tada tekao na isti način i znaće koji su to brojevi. On ovako ima manje informacija.
[ Nedeljko @ 28.07.2013. 15:16 ] @
Informacije dobijene razgovorom su u prvom slučaju:
Za Proizvod: Suma računajući sa limitom 200 zna da ja računajući sa limitom 200 ne mogu da znam brojeve.
Za Sumu: Ako Proizvod računa sa limitom 200, on ne zna da ja računajući sa limitom 200 znam da on brojeve ne zna, ali nakon tog saznanja on računajući da limitom 200 uspeva da odredi brojeve.
Daj im iste te informacije i dodatnu informaciju da brojevi nisu veći od 30 i rešiće zadatak. Druga je stvar ako im daš izmenjene informacije i onda kao neku dodatnu.
To što je neko parče teksta jezički isto, ne znači da znači isto. Mora se ceo kontekst uzeti u obzir.
[ Nedeljko @ 29.07.2013. 18:02 ] @
21. Zadatak
Da moderatori prebace raspravu o sumi i proizvodu na teme o njima, a ovde mogu da ostave link prema tamo.
Tačno ili netačno?
[ number42 @ 29.07.2013. 19:27 ] @
moze neko da postavi 21. zadatak
[ zzzz @ 30.07.2013. 00:46 ] @
Postavio bih ja još nešto iz informatike,vrlo interesantno i kontraverzno.Ali samo pod uslovom da se ovom LIKU omogući da kaki kod kuće a ne ovdje na forumu.Ili bar da mu izmet nije dugačak 50K.
Adio.
[ miki069 @ 30.07.2013. 13:15 ] @
Ko je mogaao sa uslovom "manji su od 200" da reši zadatak, a sa uslovom "manji su od 30" nije mogao da reši zadatak?
Proizvod, Suma ili Rešavač zadatka?
[ Nedeljko @ 30.07.2013. 13:53 ] @
Ovaj što se ljuti kad nije u pravu.
[ number42 @ 30.07.2013. 20:30 ] @
@zzzz,
izvinjavam se tebi i svima ako uspe da vas isprovocira bilo ko ko opstruira temu.
pokusao sam kao pokretac koliko sam mogao da to sprecim, pa valjda ce ubuduce biti ok.
moj savet je da ignorisete takve ljude ako i dalje pokusavaju, i cao.
ako se slucajno predomislis za zadatak, eto ostavljamo prazno i ceka te 21. pitanje, da postavis :)
[ number42 @ 30.07.2013. 20:33 ] @
preko ove slike su matematicki povezani maja i dali

y/n? [ number42 @ 30.07.2013. 21:37 ] @
ako treba pomoc za resavanje:
maja je 3d softver 'automatik maja', a dali je slikar salvador dali.
na slici treba da se uochi geometrijski oblik... i onda malo surfanja :)
[ darkosos @ 31.07.2013. 07:28 ] @
Pretpostavljam da se pod "opstrukcijom" na ovoj temi podrazumeva tacno resavanje zadataka :)
[ miki069 @ 31.07.2013. 09:36 ] @
Odgovor na 18. pitanje je NE.
Navedeni "kontraprimer" je neispravan.
[ number42 @ 31.07.2013. 19:42 ] @
odgovor, 22. zadatak:
yes it is.
dalija i maju povezuje teserakt tj 4-dimenziona kocka
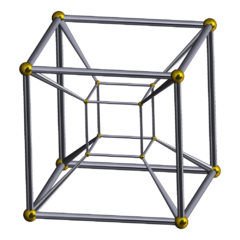
na slici salvadora dalija je prikazano raspece na rasklopljenoj 4-dimenzionoj kocki u 3-dimenzioni prostor, a 'automatic maja' je 3d softver na kome je napravljena cuvena slika teserakta koji rotira.
na vikipediji pise da su u pitanju dve rotacije. na slici se jasno vidi jedna rotacija, ali ono drugo ne znam sta je, potseca na kocku koja se smanjuje pa prolazi kroz kocku koja se povecava, pa se ova smanjuje pa prolazi kroz prethodnu, itd. nemam pojma koje je to kretanje.
slika je proglasena za sliku meseca 2007 na matematickom portalu, a 2008 je usla u finale za najbolju sliku uopste.
za dalijev prikaz je steta sto je reprodukcija jako slaba, na slici se vidi i kako je odradio perspektivu iza raspeca, a potseca otprilike na neki produzeni prostor. uglavnom cela slika je matematicko poigravanje religijskim motivima.
_____
e sad, meni ovo uopste nije jasno. mislim, zanimljiv je tesarakt kao spekulacija, ali... nema mnogo prevedenog materijala da bi se moglo jasno ukapirati o cemu se radi.
ako se islo logikom toga da utvrdi sta se nalazi izvan naseg 3d(+1) i 5 culnog poimanja, nemam pojma kako su to strpali u dimenzije.
prvo, uopste nismo sigurni da postoji ta neka shira realnost, a definitivno nismo sigurni da je mozemo kvantifikovati dimenzijama, racunski i geometrijski.
jos veca fora je to da ovo ide na jos vise dimenzija, pa se kod teorije struna pojavljuje nekih desetak...
zaista moram da se ogradim jer nisam procitao sve o hiperkocki, ali iz ono malo materijala prevedenog sa engleskog koje sam nasao na netu- cini mi se da su uzeli pogresnu analogiju (kao kod nasih uobicajenih 1d, 2d, i 3d).
ajd recimo da gresim, pa jedna dodatna dimenzija predstavlja neko prosirenje u odnosu na nase uobicajeno poimanje. sta onda predstavlja druga dodatna dimenzija? jos neko prosirenje poimanja?
znaci, poenta je da mi nikako ne mozemo znati, ako uopste postoji a verovatno da, sta je van nase moci poimanja.
stvari se postavljaju aksiomatski percepocenticno, tj grubo receno ako su akciomi polazne stvari koje uzimamo zdravo za gotovo na osnovu nase 3d(+1) i 5-culne percepcije, necemo imati isti sistem aksioma mi i neka bakterija.
i onda zamislimo stvorenja koja su u odnosu na nas kao mi u odnosu na bakterije. i ona ce imati aksiomatski sistem prilagodjen svom vidjenju sveta. mi nikako ne mozemo znati kakav je to aksiomatski sistem, niti da li uopste postoji jer osnovni parametri mogu biti promenjivi, il vec nesto trece a sto ne mozemo da zamislimo nikako.
znaci pitanje je: sta bi to tacno teserakt trebalo da predstavlja u prirodi, nama nepojmljivoj?
[ number42 @ 31.07.2013. 19:45 ] @
moze sledece, 23. zadatak ko hoce da postavi
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|