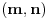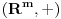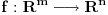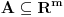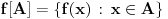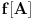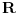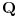[ Nedeljko @ 12.07.2013. 14:37 ] @
|
[ Nedeljko @ 12.07.2013. 16:22 ] @
[ Nedeljko @ 13.07.2013. 08:18 ] @
Samo da kažem da je u oba slučaja odgovor skup svih parova prirodnih brojeva.
[ Nedeljko @ 13.07.2013. 19:04 ] @
Ima li interesovanja za ovakve zadatke, ili da dam lakše ili nekog drugog tipa?
[ bojan_bozovic @ 13.07.2013. 19:21 ] @
Hajde, ja da pokušam...
Prvo, imamo grupu n-torki (Rn,+) i grupu m-torki (Rm,+) i neka je m=|=n Neka je n>m, imamo da je F:Rn->Rm najviše surjektivna jer postoji makar jedno n za koje postoji n-torka iz Rn bez slike u Rm (a svaka m-torka iz Rm ima original u Rn, pošto mora biti bijektivna), i to upravo svaka takva da je n>m, a ako je n<m F:Rn->Rm je najviše injektivna, jer postoji m takvo da postoji m-torka iz Rm bez originala iz Rn, i to baš svaka pri m>n ( a svaki original iz Rn mora imati sliku, ako je bijekcija). Neka je n=m, imamo bijekciju F:Rn->Rn definisanu sa F(x1...xn)=(x1...xn) koja ispunjava zahtev. Asocijativnost, zatvorenost, postojanje neutrala, i inverza sve bi trebalo da sledi iz bijektivnosti F, Sad ću da probam to da dokažem. Kako je Rn grupa, važi za x,yERn postoji (x+y)ERn - zatvorenost. Kako je F bijektivna, za svako x+yERn postoji baš jedno F(x+y)ERn. U Rn imamo neutral 0: x+0=x za svako xERn. Zato je i F(x)=F(x+0)=F(x)+F(0), pa je F(0)=0. U Rn imamo inverz (-x) za svaki xERn takvo da je (-x)+x=0. onda je: F(0)=F(-x+x)=F(-x)+F(x)=-F(x)+F(x). Asocijativnost, (x+y)+z=x+(y+z). F((x+y)+z)=F(x+y)+F(z)=F(x+y)+F(-y+y+z)=F(x)+F(y)+F(-y)+F(y+z)=F(x)+F(y+z)=F(x+(y+z)). [Ovu poruku je menjao bojan_bozovic dana 13.07.2013. u 21:49 GMT+1] [ Nedeljko @ 13.07.2013. 20:33 ] @
[ Nedeljko @ 14.07.2013. 11:17 ] @
Citat: bojan_bozovic: Neka je n>m, imamo da je F:Rn->Rm najviše surjektivna ako je n<m F:Rn->Rm je najviše injektivna Ovo nije tačno. Bijekcija između 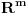 i i 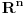 postoji. postoji.Kao što sam dokazao u prethodnoj poruci (dobro, fali račun dimenzije vektorskog prostora, što se može dodati ako neko bude pitao), izomorfizam postoji za sve 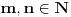 . .[ bojan_bozovic @ 14.07.2013. 11:55 ] @
Kako postoji bijekcija F:Rn->Rm pri n>m? Ako dokaz ne valja, objasni zašto, molim. Ako je n>m svaki element iz kodomena može imati original u Rn, ali ne važi da svaki element domena ima sliku u Rm (pa nije injektivno), bar ja mislim, i upravo zato bi i trebalo da bude dim(Rn)>dim(Rm) pri n>m (ako uvedemo i skalarni proizvod kao u vektorskom prostoru).
Gde grešim? [Ovu poruku je menjao bojan_bozovic dana 14.07.2013. u 13:12 GMT+1] [ Nedeljko @ 14.07.2013. 14:30 ] @
Uzmi ovakvo preslikavanje
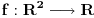 : :Neka je 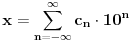 , , 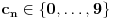 , ,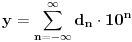 , , 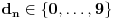 . .Pritom za svako 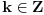 postoji postoji 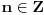 takvo da je takvo da je 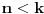 i i 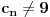 i postoji i postoji 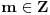 takvo da za svako takvo da za svako  važi važi 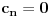 . To znači da je navedena suma dekadni razvoj broja . To znači da je navedena suma dekadni razvoj broja  koja se ne završava devetkama, a takav razvoj proizvoljnog realnog broja je jedinstven, tj. niz koja se ne završava devetkama, a takav razvoj proizvoljnog realnog broja je jedinstven, tj. niz 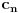 jednoznačno određen brojem jednoznačno određen brojem  . Isto pretpostavimo za niz . Isto pretpostavimo za niz 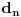 . .Neka je 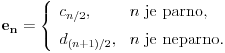 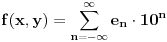 je jedna od mogućih injekcija. je jedna od mogućih injekcija.Naravno, ova injekcija nije homomorfizam (što se traži u zadatku), ali dokazuje da postoje injektivna preslikavanja iz 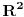 u u  . .[ Nedeljko @ 14.07.2013. 23:19 ] @
Ako ti i dalje nije jasno, slobodno napiši zašto misliš da preslikavanje iz R2 u R ne može da bude injektivno. Ako je linearno u odnosu na koeficijente iz R, onda svakako ne može biti injektivno. Međutim, nisu sva preslikavanja linearna.
[ Sonec @ 16.07.2013. 18:23 ] @
[ Nedeljko @ 16.07.2013. 18:29 ] @
Već sam to napisao.
Citat: Nedeljko: 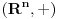 se moze posmatrati kao vektorski prostor nad poljem racionalnih brojeva dimenzije kontinuum. Vektorski prostori iste dimenzije (makar to bio i beskonacan kardinal, ali isti) su izomorfni. se moze posmatrati kao vektorski prostor nad poljem racionalnih brojeva dimenzije kontinuum. Vektorski prostori iste dimenzije (makar to bio i beskonacan kardinal, ali isti) su izomorfni.[ Sonec @ 16.07.2013. 18:31 ] @
E, vidi stvarno, nisam video (nisam ni gledao sta ste pisali (shame on me)). Dobro onda. Brm brmm
[ Nedeljko @ 16.07.2013. 22:23 ] @
Hajde da dam hint za drugi.
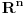 se može predstaviti kao prebrojiva disjunktna unija slika skupa se može predstaviti kao prebrojiva disjunktna unija slika skupa 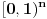 pri translacijama. Dakle, treba problem rešiti za slučaj Lebegove mere na njima. pri translacijama. Dakle, treba problem rešiti za slučaj Lebegove mere na njima.Ako je neki prostor snabdeven sigma aditivnom merom u kojoj su tačke mere nula, onda je taj prostor izomorfan prostoru koji se od tog dobija izbacivanjem najviše prebrojivog skupa tačaka. Na skupu 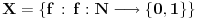 se može uvesti najmanja sigma aditivna kompletna mera koja ispunjava sledeći uslov: Za svaki izbor različitih prirodnih brojeva se može uvesti najmanja sigma aditivna kompletna mera koja ispunjava sledeći uslov: Za svaki izbor različitih prirodnih brojeva  i izbor vrednosti i izbor vrednosti 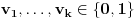 je mera skupa je mera skupa 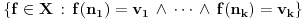 je jednaka je jednaka 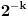 . Ona se može shvatiti i kao normiana mera na Kantorovom skupu (dakle, ne nasleđena od Lebegove) u kojoj podudarni delovi imaju istu meru, a skup tačaka Kantorovog skupa druge vrste je izomorfan sa . Ona se može shvatiti i kao normiana mera na Kantorovom skupu (dakle, ne nasleđena od Lebegove) u kojoj podudarni delovi imaju istu meru, a skup tačaka Kantorovog skupa druge vrste je izomorfan sa  sa izbačenim tačkama oblika sa izbačenim tačkama oblika 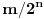 snabdevenim Lebegovom merom. Idempotentnost od snabdevenim Lebegovom merom. Idempotentnost od  se kudikamo lakše dokazuje. se kudikamo lakše dokazuje.Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|