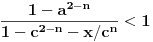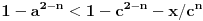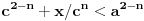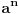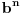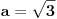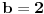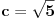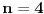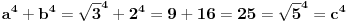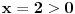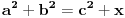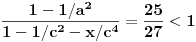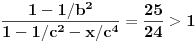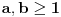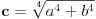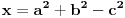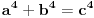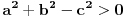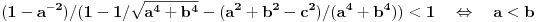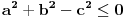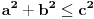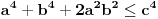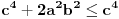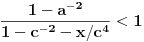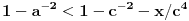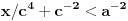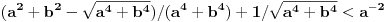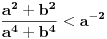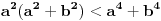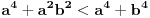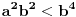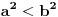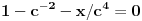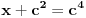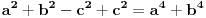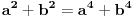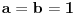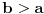|
|
[ number42 @ 17.07.2013. 17:44 ] @
|
| ovo je valjda dokaz fermata (a^n+b^n=c^n) za dva slucaja, kada su osnove pitagorine trojke, i kada je zbir osnova sa leve strane znaka jednakosti jednak osnovi s desne strane znaka jednakosti.
ali kako je ovo neverovatno prosto- ako neko moze da mi ukaze na gresku u postupku ili racunanju zahvalan unapred, ili ako je nekim cudom tacno- kako bih mogao da uopstim postupak.
uglavnom u oba slucaja se ide na istu foru.
-pitagorine trojke
(1) a^2+b^2=c^2
(2 a^n+b^n=c^n
(3) a^n-a^2+b^n-b^2=c^n-c^2
(3a) a^2((a^(n-2))-1)+b^2((b^(n-2))-1)=c^2((c^(n-2))-1)
(3b) a^2[((a^(n-2))-1)/((c^(n-2))-1)]+b^2[((b^(n-2))-1)/((c^(n-2))-1)]=c^2
_______________________________
-jednakost osnova
(4) a+b=c
(5) a^n+b^n=c^n
(6) a^n-a+b^n-b=c^n-c
(6a) a((a^(n-1))-1)+b((b^(n-1))-1)=c((c^(n-1))-1)
(6b) a[((a^(n-1))-1)/((c^(n-1))-1)]+b[((b^(n-1))-1)/((c^(n-1))-1)]=c
_______________________________
-tumacenje (za pitagorine trojke):
jednacina (1) je tacna. da bi dobili jednacinu (2) moramo svakom clanu dodati neki broj. zbir tih dodataka na levoj strani mora biti jednak dodatku na desnoj strani, a to je jednacina (3).
da bi jednacina (2) bila tacna, moraju biti tacne i jednacina (1) i (3). ali jednacina (3) nije tacna, jer kada je podelimo sa c^(n-2)-1, i uporedimo sa prvom, vidimo da prvi i drugi clan iz jednacine (1) mnozimo razlomkom koji je manji od jedan, a treci clan ostaje isti. to ne ispunjava jednakost iz prve jednacine. dakle, jednacina (3) nije tacna, samim tim ni jednacina (2), tj dokazana je fermatova teorema za slucaj pitagorinih trojki kao osnova.
_________________________________
-tumacenje (za jednakost osnova):
jednacina (4) je tacna. da bi dobili jednacinu (5), svakom clanu moramo dodati neki broj. zbir tih dodatak na levoj strani znaka jednakosti mora biti jednak dodatku na desnoj strani znaka jednakosti, a to je jednacina (6).
da bi jednacina (5) bila tacna, moraju biti tacne jednacine (4) i (6). ako jednacinu (6) podelimo sa c^(n-1)-1, i uporedimo sa jednacinom (4), vidimo da su prvi i drugi clan jednacine (4) pomnozeni razlomkom koji je manji od jedan, a da je treci clan ostao isti, a to jednostavno ne ispunjava uslov o tacnosti jednacine (4).
dakle, jednacina (6) je netacna. samim tim je i jednacina (5) netacna, tj dokazana fermatova teorema kada je zbir osnova sa leve strane znaka jednakosti jednak osnovi sa desne strane znaka jednakosti.
EDIT: ubacio sam jednacine 3a, 3b, 6a i 6b, valjda se tako lakse moze shvatiti.
[Ovu poruku je menjao number42 dana 17.07.2013. u 21:03 GMT+1] |
[ number42 @ 17.07.2013. 19:57 ] @
i, jel moze neko da ukaze na gresku ili da potvrdi tacnost? imam neke ideje za uopstenje, ali prvo da vidim da li je ovo ispravan postupak i racunanje.
inace, izostavio sam jedan deo pa mozda deluje komplikovanije, jer sam prvi put pisao opsirno pa mi se pred sami kraj slucajno sve obrisalo, pa sam popizdeo i ponovo sve napisao samo ukratko.
sta sam izostavio... da jednacine (3) i (6) mogu da se pisu i drugacije pa je jasnije
(3) a^n-a^2+b^n-b^2=c^n-c^2
<=>
(3a) a^2((a^(n-2))-1)+b^2((b^(n-2))-1)=c^2((c^(n-2))-1)
ako celu jednacinu podelimo sa c^(n-2)-1 dobijamo
(3b) a^2[((a^(n-2))-1)/((c^(n-2))-1)]+b^2[((b^(n-2))-1)/((c^(n-2))-1)]=c^2
i uporedimo je sa jednacinom
(1) a^2+b^2=c^2
vidimo da su u jednacini (3b) a^2 i b^2 pomnozeni razlomcima manjim od jedan, a c^2 je ostalo isto. a to je netacno jer je jednacina (1) tacna, pa onda je i a^n+b^n= c^n netacno u ovom slucaju.
_______________________________
6) a^n-a+b^n-b=c^n-c
<=>
(6a) a((a^(n-1))-1)+b((b^(n-1))-1)=c((c^(n-1))-1)
i ide isti postupak, sve delimo sa (c^(n-1))-1 itd...
[ number42 @ 17.07.2013. 22:09 ] @
pa dobro, pod pretpostavkom da je ovo iznad tacno, evo pokusaj uopstenja za celu fermatovu teoremu.
prvo da dam primer. ako imamo
3^n+5^n=10^n
ovo ne mozemo uklopiti u nacin resavanja iz prvog posta, jer 3,4,10 nije ni pitagorina trojka niti je 3 i 4 jednako 10.
dakle ne mozemo da pisemo
3+5=10
ali zato mozemo
3+5+2=10
ako ovo uopstimo, imamo dve jednacine
(1) a^n+b^n=c^n
(2) a+b+x=c
druga je tacna, a za prvu zelimo da utvrdimo da li je tacna
oduzmemo drugu od prve i dobijamo
(3) a^n-a+b^n-b-x=c^n-c
to je ekvivalentno
(3a) a(a^(n-1)-1)+b(b^(n-1)-1)-x=c(c^(n-1)-1)
celu jednacinu podelimo sa c^(n-1)-1 i dobijamo
(3b) a[(a^(n-1)-1)/(c^(n-1)-1)]+b[(b^(n-1)-1)/(c^(n-1)-1)]-x[1/(c^(n-1)-1)]=c
uporedimo jednacinu (3b) sa jednacinom (2) i vidimo da je od cetiri clana menjano samo prva tri a da je cetvrti (rezultat) ostao isti.
prva tri su menjana na taj nacin da su prva dva pomnozena sa razlomkom koji ima vrednost izmedju nule i jedan, a treci clan je menjan tako da je umanjen za dvostruku vrednost i pomnozen razlomkom cija je vrednost izmedju 0 i 1.
prakticno, posmatrajuci jednacinu (2) koju smo uzeli kao tacnu, vidimo da je desna strana ostala ista, a da je svaki clan na levoj strani umanjen, a to, zbog definisanosti jednacine (2) kao tacne, moze da znaci samo netacnost jednacine (3).
kako je jednacina (3) ono sto smo dodali jednacini (2) da bi dobili jednacinu (1), a kako je (2) tacna, a (3) netacna, to je i jednacina (3), tj a^n+b^n=c^n netacna, i dokazana fermatova teorema.
[ number42 @ 17.07.2013. 23:12 ] @
eh, sad sam video... uopstenje iz proslog komenta nije tacno. jednacina (2) mora da bude u obliku a+b-x=c da bi odgovarala a^n+b^n=c^n, a ne kako sam ja napisao. a za ovakvu postavku trenutno nemam ideju kako je resiti.
svejedno, mislim da su racunanje i postupak u prvom komentaru, na koji se i odnosi tema, ispravni.
[ miki069 @ 18.07.2013. 19:09 ] @
Tačna su oba dokaza specijalnih slučajeva.
Slučaj za a+b=c sledi odmah iz binomne formule.
[ number42 @ 18.07.2013. 20:36 ] @
@miki069,
hvala ti, bas si me obradovao, sad mogu da nastavim da probam da je uopstim.
ne znam sta je binomna formula, nasao sam na netu o tome al nisam bas skontao. al nema veze ako sljaka i ovako.
sto se tice uopstavanja, ako postoji kraci dokaz tj ako fermat nije lagao a mislim da nije, onda ide preko osnova a ne stepena, pretpostavljam.
ali na neki drugaciji nacin od ovog iz prvog komenta.
[ number42 @ 19.07.2013. 06:52 ] @
u prvom komentaru je bio dokaz za a^n+b^n=c^n kada je a^2+b^2=c^2.
a ovo je dokaz, ako nisam nesto negde zeznuo, za manje umesto jednako, tj kada je a^2+b^2<c^2.
to se moze pisati i kao jednacina (1)
(1) a^2+b^2+x=c^2
a opsta jednacina fermatove teoreme je
(2) a^n+b^n=c^n
saberemo ove dve i dobijamo
(3) a^n+a^2+b^n+b^2+x=c^n+c^2
jednacina (1) je tacna, a ukoliko je (3) tacna onda je i (2), i ako je (3) netacna onda je i (2).
preformulisemo jednacinu (3)
(3a) a^2(a^(n-2)+1)+b^2(b^(n-2)+1)+x=c^2(c^(n-2)+1)
podelimo sve sa c^(n-2)+1 i dobijamo
(3b) a^2 * [(a^(n-2)+1) / (c^(n-2)+1)] + b^2 * [(b^(n-2)+1) / (c^(n-2)+1)] + x * [1 / (c^(n-2)+1)] = c^2
uporedimo jednacinu (3b) i jednacinu (1).
u odnosu na jednacinu (1), u jednacini (3b) je prvi clan pomnozen razlomkom cija je vrednost od 0 do 1 dakle smanjen je, drugi clan je smanjen na isti nacin, kao i treci clan, a cetvrti clan je ostao isti.
dakle, u odnosu na tacnu jednacinu (1), u jednacini (3b) imamo desnu stranu koja je ostala ista, i levu stranu koja je smanjena, a to znaci da je jednacina (3) netacna, samim tim i jednacina (2).
tj opsti oblik fermatove teoreme a^n+b^n=c^n kada je a^2+b^2<c^2 je nemoguc.
[ number42 @ 20.07.2013. 04:58 ] @
evo resavam fermatovu teoremu (a^n+b^n=c^n) za slucaj kada je a^2+b^2>c^2, i nikako ne uspevam da dobijem kontradikciju. pokusavao sam 3-4 sata svim mogucim kombinacijama koje su mi pale na pamet, ali nista ne prolazi.
jel moze neko da da neki predlog kako se ovo moze dovrsiti? jer dokazom ovoga, zavrsava se ceo dokaz za fermata, jer sam u proslom i prvom komentaru dokazao za preostale slucajeve, a^2+b^2=c^2 i a^2+b^2<c^2.
mislim, vidi se jasno kontradikcija, ali ne mogu da je dobijem racunski precizno i nedvosmisleno.
stvari sam postavio ovako:
kada je
(1) a^p+b^p>c^p
onda ce, kako p raste, i znak da se promeni iz '>' u '<', jer rastom stepena desna strana se vise povecava od leve strane. ali kada jednom leva strana bude manja od desne, ona to i ostaje (taj poddokaz je u svega par redova, preskacem ga da smanjim komplikovanje), a to je i intuitivno jasno.
znaci, kada se jednom promeni znak (porastom stepena) u formuli (1) tako da je leva strana manja od desne, onda tako i ostaje ma koliko stepen rastao. ovo prakticno znaci da se od trenutka promene znaka iz '>' u '<' vise ne moze postici jednakost.
a to opet znaci da se jednakost ako postoji nalazi neposredno pre tog stepena, znaci ako menja znak u '<' na stepenu 'n+1', onda je jednakost na stepenu 'n', a na stepenu 'n-1' je i dalje znak '>'.
ili brojkama:
(2) a^2+b^2>c^2
(3) a^(n-1)+b^(n-1)>c^(n-1)
(4) a^n+b^n=c^n
(5) a^(n+1)+b^(n+1)<c(n+1)
ovo se jednacinama moze napisati i kao:
(6) a^2+b^2-x=c^2
(7) a^(n-1)+b^(n-1)-z=c^(n-1)
(8) a^n+b^n=c^n
(9) a^(n+1)+b^(n+1)+y=c^(n+1)
formule (6), (7), i (9) su tacne, a za (8) ispitujemo tacnost, tj da li postoji.
nisam siguran da je i formula (7) nuzna, ali nema veze, ne moze da skodi jer je tacna.
i sad kako god da ih kombinujem, sabiram oduzimam i sl, dobijam jasno vidljivu kontradikciju, ali ne i matematicki preciznu. i samim tim ni dokaz ne mogu da dobijem.
ako je neko dobar s racunanjem i ima ideju kako ovo izvesti, svaki predlog je dobrodosao.
[Ovu poruku je menjao number42 dana 20.07.2013. u 06:15 GMT+1]
[ number42 @ 22.07.2013. 00:15 ] @
pa da pokusam dokaz za a^2+b^2-x=c^2 za fermatovu teoremu, kada je x>c^n tj x>a^n+b^n, a to je za pola preostalih slucajeva.
imamo dve formule
(1) a^2+b^2-x=c^2
(2) a^n+b^n=c^n
prva jednacina je tacna, a ispitujemo tacnost druge.
podelimo prvu s drugom, ili (1):(2)
(3) (a^2+b^2-x)/(a^n+b^n)=(c^2)/(c^n)
ovo moze da se pise i kao
(4) (a^2+b^2)/(a^n+b^n) - x/((a^n+b^n) = (c^2)/(c^n)
ako je jednacina (4) tj (3) netacna, onda je netacna i trazena jednacina (2).
prvi clan jednacine (4) je razlomak izmedju 0 i 1, drugi clan je pozitivan broj veci od 1 (jer je po pocetnoj postavci slucaj kad je x>a^n+b^n), i treci clan, s desne strane znaka jednakosti, je razlomak izmedju 0 i 1.
ovo je nemoguce jer - razlomak izmedju 0 i 1, minus pozitivan broj veci od 1, daje negativnu vrednost, a u ovom slucaju vidimo da nije tako nego daje pozitivnu.
znaci ovo je dokaz fermata, ako negde nije greska, za slucaj kad je x>c^n.
ostalo je jos "samo" za slucaj x<c^n.
[ number42 @ 22.07.2013. 17:58 ] @
upravo sam skontao da x mora biti manje od
a^2 i b^2
u izrazu
a^2+b^2-x=c^2.
e bas sam pametan....
koliko vidim ovo se svodi na to da postoje hiljade kombinacija, i onda treba naci nekoliko koje kombinovane daju kontradikciju. i kad se to zavrsi ceo dokaz se svodi u nekih tridesetak redova.
a to je ono bas smor. uopste se ne isplati petljati s ovim.
[ number42 @ 28.07.2013. 16:50 ] @
ispravka u postavci za treci slucaj
Citat: a^p+b^p>c^p
rastom stepena desna strana se vise povecava od leve strane
ovo nije tacno, npr brojevi 8, 10, i 11 kao a,b i c ne ispunjavaju ovaj uslov.
8^2+10^2-11^2=43
8^3+10^3-11^3=181
8^4+10^4-11^4=-545
ili 98, 99, i 100 kao a,b i c
98^2+99^2-100^2=9405
98^3+99^3-100^3=911491
98^4+99^4-100^4=88296417 [ number42 @ 02.08.2013. 14:28 ] @
evo resio sam fermata a^n+b^n=c^n za trecinu treceg slucaja, kada je a^2+b^2>c^2.
ako je racun tacan, to bi ukupno bilo dokazano jedno 7/9 teoreme.
znaci imamo ovako
(1) a^2+b^2>c^2
podelimo sa c^2
(2) (a/c)^2+(b/c)^2>1
kako je a<c i b<c, onda su i a/c i b/c brojevi koji nisu veci od jedan, ma koliko ih stepenovali, pa i njihov zbir mora da bude manji od dva
(3) (a/c)^2+(b/c)^2<2
pomnozimo sve sa c^2 i imamo
(4) a^2+b^2<2c^2
ili
(5) a^2+b^2+x=2c^2
osnovna jednacina fermata
(6) a^n+b^n=c^n
saberemo (5) i (6)
(7) a^n+a^2+b^n+b^2+x=c^n+2c^2
preformulisemo
(8) a^n * (1+1/a^(n-2)) + b^n * (1+1/b^(n-2)) + x = c^n * (1+2/c^(n-2))
podelimo sve sa (1+2/c^(n-2)) i imamo
(9) a^n * (1+1/a^(n-2)) / (1+2/c^(n-2)) + b^n * (1+1/b^(n-2)) / (1+2/c^(n-2)) + x * (1/(1+2/c^(n-2)) = c^n
uporedimo jednacine (9) i (6)
imamo 3 slucaja
a) da je a^(n-2) < (c^(n-2))/2, i b^(n-2) < (c^(n-2))/2.
u tom slucaju se prvi clan povecava, drugi clan se takodje povecava, treci clan kojeg nemamo u jednacini (6) se pojavljuje kao pozitivan, a rezultat tj desna strana ostaje ista. znaci, imamo kontradikciju.
b) drugi slucaj je da je a^(n-2) > (c^(n-2))/2, i b^(n-2) > (c^(n-2))/2. nisam siguran ali mislim da se svodi na slucaj a^2+b^2<c^2 koji sam vec dokazao u nekom prethodnom komentaru. svejedno bih trebao da dokazem da se svodi na to, al nek bude da nemam odgovor na drugi slucaj.
c) treci slucaj je kada je a^(n-2) manje od (c^(n-2))/2, a b^(n-2) vece od (c^(n-2))/2. u ovom slucaju nemam nikakvu predstavu sta da radim.
znaci tu su ostala jos ove 2/9, pa ako neko ima ideju kako da dovrsi, posto je mene smorilo jako :), slobodno nek resava.
[Ovu poruku je menjao number42 dana 02.08.2013. u 21:11 GMT+1]
[ number42 @ 02.08.2013. 20:15 ] @
ispravka u proslom komentaru- pogresio sam znakove '<' i '>' u slucajevima a) i b), pa sam ispravio.
[ number42 @ 04.08.2013. 08:03 ] @
i evo dovrsio sam dokazivanje cele fermatove teoreme.
al kako je ovo sve neverovatno prosto, ako neko ko se dobro razume u racun moze samo da pregleda racunanje i rezonovanje, i vidi sta sam opet zeznuo  ko po obicaju...
mislim, nemoguce da je ceo dokaz u manje od 30 redova formula...
znaci, zamislio sam ovako:
svodi se na tri slucaja gde se trazi kontradikcija, i za prva dva slucaja sam vec napisao, a sledi i za treci:
1.slucaj, nemogucnost a^n+b^n=c^n kada je a^2+b^2=c^2
http://www.elitesecurity.org/t467352-0#3322875
2.slucaj, nemogucnost a^n+b^n=c^n kada je a^2+b^2<c^2
http://www.elitesecurity.org/t467352-0#3323369
3. i ovo je treci slucaj za nemogucnost a^n+b^n=c^n kada je a^2+b^2>c^2
dokazivanje za trecu tj zadnju varijantu bi redom islo ovako:
(1) a^n+b^n=c^n
(2) a^2+b^2-x=c^2
preformulisemo (2)
(3) a^2+b^2=c^2+x
oduzmemo (3) od (1)
(4) a^n-a^2+b^n-b^2=c^n-c^2-x
preformulisemo (4)
(5) a^n * (1 - 1/(a^(n-2))) + b^n * (1 - 1/(b^(n-2))) = c^n * (1 - 1/(c^(n-2)) - x/(c^n))
podelimo sve sa (1 - 1/(c^(n-2)) - x/(c^n)) i dobijemo
(6) a^n * [(1 - 1/(a^(n-2))) / (1 - 1/(c^(n-2)) - x/(c^n))] + b^n * [(1 - 1/(b^(n-2))) / (1 - 1/(c^(n-2)) - x/(c^n))] = c^n
uporedimo (6) i (1) i vidimo da je u odnosu na (1), u (6) doslo do smanjenja prvog clana, i smanjenja drugog clana, dakle leve strane, dok je treci clan, tj desna strana, ostala ista. a to znaci i kontradikciju, tj nemogucnost fermatovog izraza i za treci slucaj, kada je a^2+b^2>c^2.
i to je sve.
al neverovatno je da ceo dokaz fermata moze da stane u manje od 30 redova, mislim na formule a ne tekst koji je opisnog karaktera, znaci na nekih... pola stranice A4.
znaci, gde je greska u izvodjenju?
[ Nedeljko @ 04.08.2013. 09:19 ] @
Živo me zanima na osnovu čega je
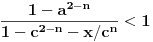 .
Ovo je inače ekvivalentno sa
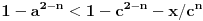 ,
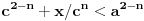 .
I? Kako dalje? Na osnovu čega su koeficijenti uz 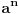 i 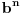 manji od 1?
Da vidimo na primeru realnih brojeva (jer naravno da sa prirodnim ne može da se napravi kontraprimer, jer je velika Fermaova teorema tačna):
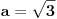 , 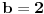 , 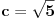 , 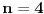 .
Svakako je
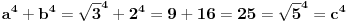 .
Za 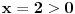 je
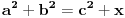 .
Da izračunamo koeficijente:
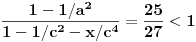 ,
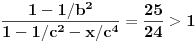 ,
što znači da prvi koeficijent manji, a drugi veći od 1.
Isti postupak se može sprovesti polazeći od bilo kog para pozitivnih brojeva 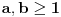 birajući
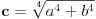 , 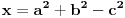
jer iz 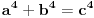 , što važi na osnovu izbora broja  , sledi 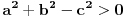 , kao i da je
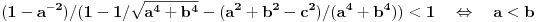 ,
pa ne mogu oba koeficijenta biti manja od jedan ili oba veća. Ako neko bude tražio, ovo mogu da dokažem.
Dakle, potrebna nejednakost svakako ne važi za realne brojeve veće od 1 ili od neke druge granice, pa se u njenom dokazivanju mora na neki način iskoristiti činjenica da su baš prirodni brojevi u pitanju.
Kako?
[Ovu poruku je menjao Nedeljko dana 04.08.2013. u 10:32 GMT+1][ number42 @ 04.08.2013. 14:39 ] @
i evo cim sam opet malo razmislio, vidim gde je greska. pretpostavio sam da se prvi i drugi clan smanjuju, a ako ne, onda se povecavaju, svejedno se javlja kontradikcija.
uopste mi nije palo na pamet dok sam pisao, da su a^n i b^n razliciti, i da bi jedan clan mogao da se povecava a drugi da se smanjuje, i da nema kontradikcije.
nego, kako god da se okrene, ovaj treci slucaj nema kontradikcije. a to je vrlo verovatno zbog toga jer je fermatova jednacina zapravo nekada tacna, ali za brojeve koji nisu celi. recimo razlomke, decimalne, negativne.
e sad treba promenjive a,b,c,n definisati kao cele pozitivne kroz jednacine. to bi moglo biti odradjeno da postoji neki izraz koji je generator celih pozitivnih brojeva, i onda se samo zameni umesto promenjivih.
ali, koliko mi je poznato takav generator ne postoji, pa to otpada.
moze da se pokusa pozitivna celobrojenost preko c^2, npr c^(n+2) pa podeljeno sa c^n, al opet ne uspevam da dobijem nista konkretno, jer verovatno a,b, i c ucestvuju kao neki razlomci, iracionalni, sta li.
mozda je najlaksa metoda odraditi racunarski, jer se mogu uneti parametri da su promenjive celi brojevi veci od 2, i to je to. e ako se ni onda ne dobija kontradikcija, onda... nemam pojma.
a moze da se odradi i preko onog metoda opadajucih koeficijenata, ili stepena, il sta vec, koju je smislio fermat, pa da da neke rezultate. bas cu da pogledam o cemu se radi.
[ Nedeljko @ 04.08.2013. 15:00 ] @
Ako je 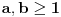 , 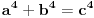 i 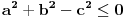 , onda je
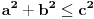
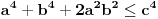 ,
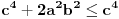 ,
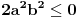 ,
što protivreči uslovu 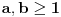 .
Dakle, za ma koje realne 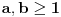 , 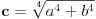 i 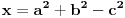 je
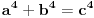 ,
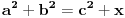 ,
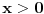 .
Pretpostavimo da je 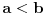 i dokažimo
(1) 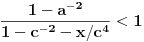 ,
odnosno
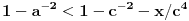 ,
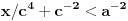 ,
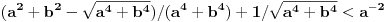 ,
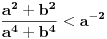 ,
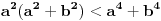 ,
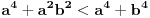 ,
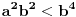 ,
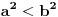 ,
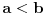 .
Još samo da dokažemo da je (1) definisano, tj. da imenilac nije nula. U suprotnom je
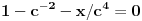 ,
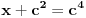 ,
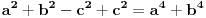 ,
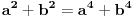 .
Za 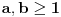 ovo je moguće samo za 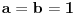 .
Na analogan način se iz 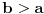 izvodi da je drugi koeficijent veći od 1.
Dakle, ovaj dokaz bez dodatnih obrazloženja (u kojima se na neki način mora iskoristiti činjenica da se radi o prirodnim brojevima) ne prolazi ni za 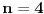 . [ number42 @ 07.08.2013. 07:28 ] @
eh, zaboravio sam da poentiram u proslom komentaru. znaci ceo dokaz kada je a=b u a^n+b^n=c^n
znaci samo prepisujem iz pretproslog komenta:
(1) a^n+b^n=c^n
(2) a^2+b^2-x=c^2
preformulisemo (2)
(3) a^2+b^2=c^2+x
oduzmemo (3) od (1)
(4) a^n-a^2+b^n-b^2=c^n-c^2-x
preformulisemo (4)
(5) a^n * (1 - 1/(a^(n-2))) + b^n * (1 - 1/(b^(n-2))) = c^n * (1 - 1/(c^(n-2)) - x/(c^n))
podelimo sve sa (1 - 1/(c^(n-2)) - x/(c^n)) i dobijemo
(6) a^n * [(1 - 1/(a^(n-2))) / (1 - 1/(c^(n-2)) - x/(c^n))] + b^n * [(1 - 1/(b^(n-2))) / (1 - 1/(c^(n-2)) - x/(c^n))] = c^n
i sada ako znamo da je a=b, jasno se vidi kontradikcija u poredjenju (6) i (1), prvi i drugi clan su promenjeni identicno, a treci clan je ostao isti.
prvi i drugi slucaj sam dokazao ranije (linkovi u pretproslom komentu), i tako sam u celini dokazao fermata za slucaj kada je a=b.
i konacno dokaz, istina parcijalan, nakon 20 dana po par sati mucenja zvrljanjem o ovome.
jeeeaaah 
tooo!  [ number42 @ 13.08.2013. 21:22 ] @
evo bas mi nesto sad palo na pamet u vezi uopstavanja, tj za treci slucaj.
a to je kada je nemogucnost fermata za a^2+b^2>c^2.
pa evo na brzinu: do sada je uglavnom u proslim komentima islo oduzimanje, znaci a^2+b^2-x=c^2 i ne moze se dobiti kontradikcija. ali zasto ne pokusati sa deljenjem, jer svodi se na isto?
npr, a^2+b^2>c^2 moze da se pise i kao (a^2)/x+b^2=c^2.
znaci islo bi
(1) (a^2)/x+b^2=c^2
(2) a^n+b^n=c^n
saberemo (1) i (2)
(3) (a^2)/x+a^n+b^2+b^n=c^2+c^n
preformulisemo
(4) a^n * (a^(2-n)/x+1) + b^n * (b^(2-n)+1)=c^n * (c^(2-n)+1)
sve podelimo sa (c^(2-n)+1)
(5) a^n * [(a^(2-n)/x+1) / (c^(2-n)+1)] + b^2 * [(b^(2-n)+1) / (c^(2-n)+1)] = c^n
uporedimo (5) i (2) i vidimo da se drugi clan povecava, treci ostaje isti, al treba utvrditi sta se desava sa prvim clanom.
treba videti da li je (a^(2-n)/x vece od c^(2-n), ako jeste onda ima kontradikcije, a svakako znamo da je x manje od a^2 u prvom clanu...
i x se krece u intervalu od 1 do a^2, a iz gornje nejednacine vidimo da se kontradikcija javlja kada je x < c^(n-2) / a^(n-2).
e sad zasto je nemoguce da x bude vece od c^(n-2) / a^(n-2) nemam pojma,
(ispravka, prepravljeno n-2 umesto n)
tako da...
nista.
[Ovu poruku je menjao number42 dana 14.08.2013. u 16:03 GMT+1]
[ number42 @ 14.08.2013. 14:30 ] @
ispravka za pretprosli komentar.
ne moze da bude dokaz za slucaj kada je a=b, jer bi se na istu foru mogla dokazati cela fermatova, jer se leva strana uvek moze svesti na zbir neka dva ista stepenovana broja.
[ number42 @ 05.09.2013. 17:12 ] @
skontao sam da se treci slucaj treba svesti samo na dokazivanje za uzajamno proste clanove, jer se dokazivanjem za njih automatski dokazuje i za uzajamno slozene (tj pomnozene nekim brojem)
a^2+b^2-x=c^2
a^n+b^n=c^n
jer iz fermatove jednacine sledi da clanovi mogu da budu samo uzajamno prosti, ili uzajamno slozeni koji mogu da se svedu na uzajamno proste deljenjem cele jednacine, jer u suprotnom nije tacna u startu.
a moze da koristi jer iz toga sledi da je x, odnosno velicina za koju je leva strana veca od desne u prvoj jednacini- uvek paran. jer za parnost kod uzajamno prostih clanova ima samo dve varijante
a b c
n n p
n p n
iz cega sledi da je x uvek parno.
e sad trenutno ne znam sta dalje s ovim  ... al mozda moze da koristi u dokazivanju.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|