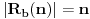
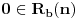
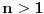
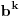
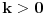
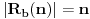
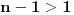
Ako je , onda je zbog je neki stepen broja deljiv sa , odnosno za brojevi i nisu uzajamno prosti. No, u tom slučaju ni brojevi nisu uzajamno prosti sa za , odnosno zbog ne postoje prirodni brojevi manji od koji su uzajamno prosti sa osim jedinice. Obzirom da su i uzajamno prosti, odatle sledi da nije . Dakle, .

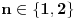
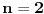
Za broj je potpuno proizvoljan, a za je proizvoljan paran broj.

_{[Ovu poruku je menjao Nedeljko dana 01.08.2013. u 00:53 GMT+1]}

Tako je, to je resenje. Ja bih samo dodatno objasnio korak u kome se dolazi do zakljucka da svi brojevi manji od (osim 1) nisu uzajamno prosti sa : posto brojevi nisu uzajamno prosti sa , to vazi i za brojeve (zapravo se najveci zajednicki delilac upravo tako moze naci, preko ostatka - Euklidov algoritam). Ali posto pogadja sve brojeve manje od n, na osnovu postavke zadatka, dobija se trazeni zakljucak.