Evo gde sam pogrešio:
Citat:
Nedeljko: Ukoliko je zamišljeni broj jednak
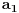
, onda je
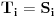
za svako
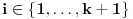
To je slučaj da je igrač A govorio isključivo istinu. Ako je malo i lagao, onda je
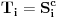
za

takvo da je slagao na

-tom pitanju.
Da napišem tačno rešenje zadatka:
Igrač B treba da postavi seriju od

pitanja
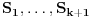
tako da bude
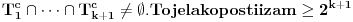
, ali treba dokazati da je to moguće za
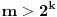
. Igrač B može da pretpostavi da je zamišljeni broj jednak
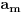
i da planira postavljanje pitanja
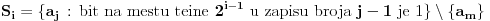
,
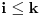
.
Ako uvek dobije odgovor "ne", onda skup

ima bar dva elementa,
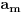
i tačno jedan iz skupa
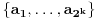
. Onda je lako izabrati pitanje
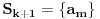
i svakako će biti
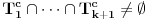
. Za odbacivanje elemenata ovog skupa nam ne treba pretpostavka da je zamišljeni broj jednak
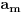
jer bar jedan od ovih
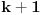
odgovora mora biti tačan.
Ako li pak jednom kaže "da", recimo na

-tom pitanju, onda igrač B zapamti to pitanje i taj skup za koji je pitao označi sa

prekida pitanja po planiranom nizu i postavlja novi niz od

pitanja znajući da je igrač A upravo slagao i da na narednih

pitanja mora dati bar jedan tačan odgovor, a tada je lako postaviti

pitanja
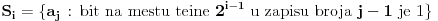
tako da bude
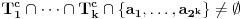
, a samim tim i
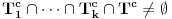
, u kom slučaju igrač B može eliminisati elemente skupa

. Opet, za odbacivanje elemenata ovog skupa nam ne treba pretpostavka da je zamišljeni broj jednak
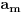
jer bar jedan od ovih
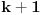
odgovora mora biti tačan.
Ukoliko se desi da pri ovoj strategiji ipak bude
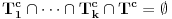
, to znači da pretpostavka da je zamišljeni broj jednak
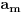
nije tačna, pa možemo njega odbaciti.
Stoga igrač B može da sužava skup mogućnosti dokle god ima više od
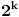
elemenata, pa ako je
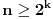
, on može kada broj mogućnosti padne na ne više od
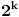
da stane, da se opredeli baš za taj skup i da pobedi.
Napisaću kasnije rešenje zadatka pod 2.