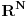
, gde je skup svih ograničenih realnih nizova sa uniformnom normom.

.

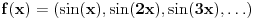
Dokažimo da funkcija nije neprekidna u tački .

.

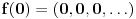
Izaberimo niz .

.

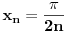
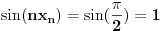
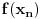
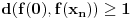
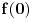
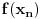
Dakle, je niz koji na -tom mestu ima jedinicu, pa je . Štaviše, obzirom da su na svim mestima u nizu nule, a u nizu brojevi po apsolutnoj vrednosti ne veći od , to je .

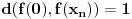
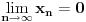
Međutim, . Stoga funkcija nije neprekidna.

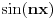
Sa druge strane, -ta projekcija funkcije je što je svakako neprekidna funkcija.

_{[Ovu poruku je menjao Nedeljko dana 17.08.2013. u 11:40 GMT+1]}

Hvala