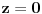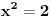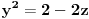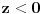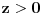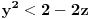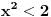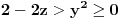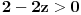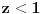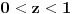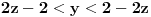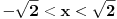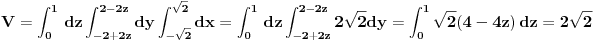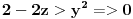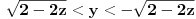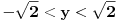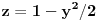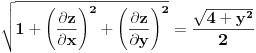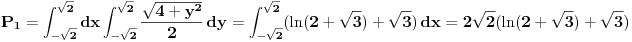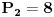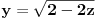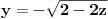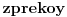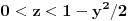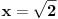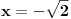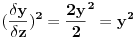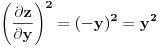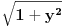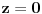
Za početak ti trebaju nejednačine, tj. za svaku jednakost (ravan Oxy ima jednačinu ) treba da pogodiš znak nejednakosti kojim treba da zameniš znak jednakosti u njoj. To se bira tako da sistem sve tri nejednačine ima rešenja, ali da skup rešenje predstavlja ograničenu oblast. Najpre primeti da se te dve jednačine mogu zameniti sledećim:

,
.

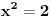
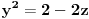
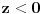
Ako bi bilo , onda bi za bilo proizvoljno velikih mogućnosti, pa oblast ne bi bila ograničena. Stoga je

.

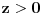
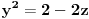
Ako bi u jednačini zamenio znak jednakosti znakom , opet bi bilo proizvoljno velikih mogućnosti za . Stoga je

.

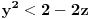
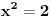
Slično tome, ne možemo staviti znak ni umesto znaka jednakosti u jednačini jer bi bilo proizvoljno velikih vrednosti za . Dakle, sistem nejednakosti glasi

,
,
.

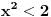
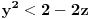
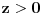
Da vidimo kako se kreću granice od za tačke koje mogu da zadovolje ovaj sistem. Obzirom da je

,

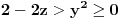
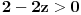
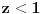
važi , odnosno . Uz uslov po iz sistema dobijamo da je

.

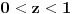
Zamislimo da smo fiksirali i ispitajmo kako se kreću granice od za tu fiksiranu vrednost od .

.

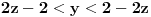
Zamislimo da smo fiksirali i i ispitajmo opseg vrednosti za za te fiksirane vrednosti od i .

.

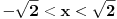
Dakle,

.

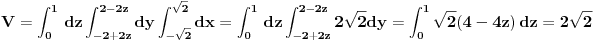
Nedeljko, hvala na brzom odgovoru. Za dva dana mi je ispit, pa mi mnogo znači. Sad mi je dosta jasnije. Ako možete da mi pomognete i oko površine preseka, ako ne-nema veze. Još jednom hvala

Edit: jedno pitanje: Imamo , da bi za granice po y imali . Gde je "nestao" kvadrat sa y, i zar granice ne bi trebale biti ?

<sub>[Ovu poruku je menjao cadjo33 dana 22.08.2013. u 20:36 GMT+1]

[Ovu poruku je menjao cadjo33 dana 22.08.2013. u 20:37 GMT+1]</sub>

Jeste, treba kvadratni koren.

Dakle,

,
,
,

Površinski element je .

.

To ti je jedna od šest površi. Druga je

,
,
.

.

Naredne dve dobijaš kada izračunaš opsege za (nezavisno) i (preko ), a zameniš svakom od dve granice koje zavise od i .

,
,
,

,
,
.

Poslednje dve dobijaš kada npr. izračunaš opsege za nezavsino, za i onda zameniš krajnjim vrednostima u zavisnosti od i .

,
,
,

,
,
.

Hvala za površine. Imam još samo jedno pitanje: za prvi površinski element, zar ne bi trebalo ? Slabo mi ide Tex, ali razumete sta mislim. pozdrav

Ako je , onda je

,

pa je površinski element .

Imam problem oko zadatka sa poslednjeg roka. Da ne otvaram novu temu postavicu ga ovdje.



Asistent mi je rekao da je najlakše da izračunam zapreminu ovog odsječka konusa i oduzmem od zapremine konusa


To su ovi osjenčeni djelovi

Svaka pomoć je dobrodošla.
Pozdrav