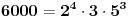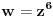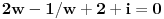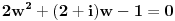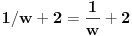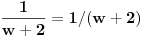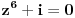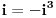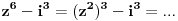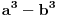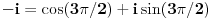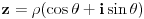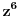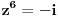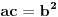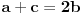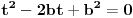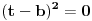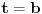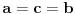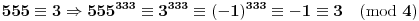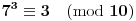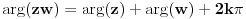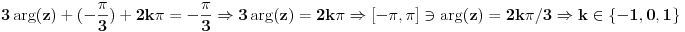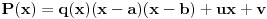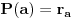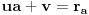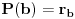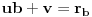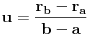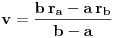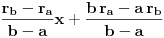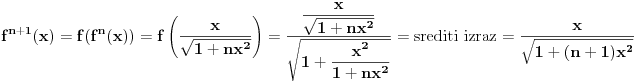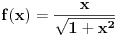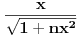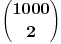[ dovlla @ 25.08.2013. 20:30 ] @
|
| Koliko ima sestocifrenih prirodnih brojeva c1c2c3c4c5c6 za koje vazi c1<=c2<=c3<=c4<=c5<=c6.Treba neko da mi potvrdi da li se ovde radi o varijacijama sa ponavljanjem od 9 elemenata(1,2,3...9) klase 6(jer se radi o sestocifrenom broju) pa bi resenje trebalo da bude 9^6 jer se ne koriste svi elementi a poredak je bitan medju izabranim elementima. |
[ Nedeljko @ 25.08.2013. 21:51 ] @
Nije dobro urađen.
Probaj da posmatraš razlike uzastopnih elemenata. Dobićeš da brojeva ima koliko i predstavljanja nekoliko brojeva kao zbira celih nenegativnih brojeva. Onda probaj da nađeš rekurentnu formulu za broj predstavljanja datog celog broja kao zbira određenog broja nenegativnih celih brojeva.
[ dovlla @ 25.08.2013. 23:16 ] @
Ako imate vremena bio bih vam zahvalan ako bi ste te to mogli detaljnije da mi pojasnite jer zaista ne znam koje brojeve da posmatram i kako da odredim rekurentnu formulu.Pretpostavljam da se ova rekurentna formula odnosi na nizove i redove.
[ kingW3 @ 26.08.2013. 00:12 ] @
Gledaj to ovako za broj 11111c6 ima 9 kombinacija za c6 a za 11112c6 ima 8 kombinacija(tj. za jednu manje) itd. gledaj to dalje za 1112c5c6
koliko resenja ima ovo?Za koliko manje od rešenja za c4=1?Posle ovoga ćeš lako naći i za 1113 i rešenje zadatka.
Pošto sam shvatio da nije tako lako zaključiti šta sam hteo da kažem
Za c5 od 1 do 9 ima 9+8+7+...+1 tj. po gausu 9*10/2=45
Sad za c4 od 1 do 9 ima 45+(45-9)+(45-9-8)=45+36+28+21+15+10+6+3+1=165
Za c3 od 1 do 9 165-45+165-(45-9)
Pošto se tako ponavlja može da se ide i supratno sabiranjem(meni lakše)
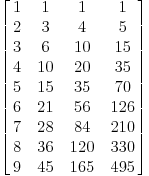
Napravio sam tablicu i počeo da sabiram ove iz druge kolone sa one iz prve
1,(1+2),1+2+3,onda iz treće kolone u drugu 1,1+1+2,1+1+2+1+2+3,i tako do ove zadnje kolone kad sabereš sve iz te kolone dobiješ 3003
Verujem da ovo moje može da se postavi na lakši način al' ne mogu sad da ražmišljam o tome.
[Ovu poruku je menjao kingW3 dana 26.08.2013. u 10:50 GMT+1][ Nedeljko @ 26.08.2013. 00:21 ] @
a1=c1-1
a2=c2-c1
a3=c3-c2
a4=c4-c3
a5=c5-c4
a6=c6-c5
Po uslovima zadatka brojevi a1,...,a6 su celi nenegativni i zbir (c6-1) im nije veći od 8.
P(n,k) je broj predstavljanja broja n kao zbira k celih nenegativnih brojeva. Takva predstavljanja za k>0 mogu prema prvom proju u zbiru biti
ona koja počinju nulom (ima ih P(n,k-1)),
...
ona koja počinju sa n (ima tačno jedno takvo, što je isto što i P(0,k-1)).
Dakle,
P(n,k)=P(n,k-1)+...+P(0,k-1)
=(P(n,k-2)+...+P(0,k-2))+...+P(0,k-2)=P(n,k-2)+2P(n-1,k-2)+...+(n+1)P(0,k-2)
=(P(n,k-3)+...+P(0,k-3))+2(P(n-1,k-3)+...+P(0,k-3))+...+(n+1)P(0,k-3)=P(n,k-3)+(1+2)P(n-1,k-3)+...+(1+...+(n+1))P(0,k-3)=(2 nad 2)P(n,k-3)+...+(n+2 nad 2)P(0,k-3)
=(2 nad 2)(P(n,k-4)+...+P(0,k-4))+...+(n+2 nad 2)P(0,k-4)=...=(3 nad 3)P(n,k-4)+...+(n+3 nad 3)P(0,k-4)
...
=(k-2 nad k-2)P(n,1)+...+(n+k-2 nad k-2)P(0,1)
=(k-2 nad k-2)+...+(n+k-2 nad k-2)
=(n+k-1 nad k-1).
Za ovo treba dokazati formulu
(k nad k)+...+(n nad k)=(n+1 nad k+1),
koja se lako dokazuje indukcijom po n.
Rešenje zadatka je
P(0,6)+...+P(8,6)=(5 nad 5)+...+(13 nad 5)=(14 nad 6)=3003.
[ dovlla @ 26.08.2013. 08:28 ] @
Hvala na brzim odgovorima.
[ dovlla @ 27.08.2013. 08:31 ] @
Da ne otvaram ponovo temu postavicu ovde jos jedan zadatak:Koliko ima cetvorki (a1,a2,a3,a4) koje zadovoljavaju uslov a1*a2*a3*a4=6000.Dosao sam do zakljucka da je postoje 4 vrste resenja:1)3 broja su neparna i 1 paran,2)2 neparna i 2 parna,3)1 neparan i 3 parna,4)4 parna broja ali ne znam kako da iskoristim ovo za dalje resavanje zadatka.
[ Nedeljko @ 27.08.2013. 09:15 ] @
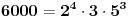 . [ dovlla @ 27.08.2013. 11:08 ] @
Nije mi palo na pamet da idem redom dok moze po stepenima dvojke pa na dalje.Sada je lako odrediti trazene cetvorke hvala puno.
[ Nedeljko @ 27.08.2013. 13:44 ] @
Uradi prvo za 2^4. Treba ti broj četvorki celih nenegativnih brojeva takav da im je zbir jednak 4. P(4,4)=(7 nad 3)=35.
Zatim uradi za 3^1. P(1,4)=(4 nad 3)=4, što je i inače očigledno.
Zatim za 5^3. P(3,4)=(6 nad 3)=20.
E, onda izmnožiš ovo troje.
35*4*20=2800.
[ dovlla @ 27.08.2013. 16:56 ] @
Imam problema sa jednacinom 2z^6-1/z^6+2=-i u skupu C.Kada prebacim z^6 na jednu stranu ostane mi 1-2i/2+i pa sam pomnozio sa 2-i/2-i da bih racionalisao pa ostaje da je z^6=-i odnosno da je z^6+i=0.E sad mislio sam da uvedem da je z=x+iy pa da posle sredjivanja realni deo kao i imaginarni stavim da su nula i da resavam kao dve jednacine ali se izraz komplikuje pa me interesuje da li postoji neko elegantnije resenje.
[ Nedeljko @ 27.08.2013. 17:26 ] @
Za 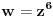 je
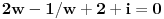 ,
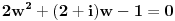 .
Je li sada lakše? [ dovlla @ 27.08.2013. 17:57 ] @
Da u redu je.Samo nadjem korene ove kvadratne jednacine i posle samo zamenim w za z^6.Hvala.
[ dovlla @ 27.08.2013. 18:28 ] @
Posto sam bio napolju kad sam citao poruku nisam obratio paznju pa moram da pitam kako dobijate 2w^2+(2+i)w-1=0 iz 2w-1/w+2=-i kada se nakon mnozenja sa w+2 dobija 2i+(2+i)w-1=0.
[ Nedeljko @ 27.08.2013. 18:45 ] @
Obzirom da se pojavljuje 1/w, nula nije rešenje, pa se množenjem sa w dobija ekvivalentna jednačina.
[ Nedeljko @ 27.08.2013. 18:46 ] @
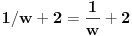 ,
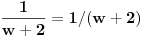 . [ dovlla @ 27.08.2013. 19:04 ] @
Izvinjavam se uopste nisam obracao paznju na zagrade.Molim vas da mi ne zamerite posto pisem sa telefona.Pravilna postavka treba da ide (2z^6-1)/(z^6+2)=-i.Jos jednom se izvinjavam bilo je nenamerno.
[ dovlla @ 27.08.2013. 19:49 ] @
Dakle da ponovim (2z^6-1)/(z^6+2)=-i.Nakon izdvajanja dobijam da je z^6=(1-2i)/(2+i) pa nakon mnozenja sa (2-i)/(2-i) dobijam da je z^6=-i odnosno z^6+i=0.
[ Sonec @ 27.08.2013. 20:36 ] @
Jel problem da resis 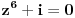 ? Ako je to, primeti da je 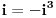 , pa je nasa jednacina u stvari 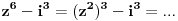 (seti se cemu je jednako 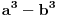 ) i posle ces lako naci sva resenja. Il ako neces preko trikova, onda predstavi 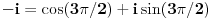 i 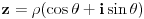 i seti se Moavrove formule (da bi nasao 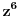 ) i vrati se na jednacinu 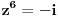 . [ dovlla @ 27.08.2013. 21:16 ] @
Hvala.Nisam mogao da se setim za ovo da je i=-i^3.
[ dovlla @ 28.08.2013. 07:39 ] @
Niz (xn) je istovremeno i aritmeticka i geometrijska progresija.Ako je x1234=1234 odrediti zbir prva 1234 clana.Naime vazi da je a1+(k-1)*d=a1*q^
(k-1) za svako k>=2, k iz N odavde je (q^(k-1)-1)/(k-1)=d/
a1=const, pa kad
diferenciram po k dobijem
jednacinu po k gde q
mora biti 1 da bi njena vrednost
bila 0 za svako k doduse u R ali negde gresim ocigledno.
[ darkosos @ 28.08.2013. 08:00 ] @
To je ok: ako su a, b i c istovremeno clanovi i AP i GP onda je 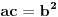 i 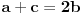 , pa su a i c resenja jednacine 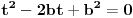 ali to je isto sto i 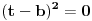 pa je jedino resenje 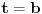 , odnosno 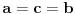 .
[Ovu poruku je menjao darkosos dana 28.08.2013. u 09:13 GMT+1][ dovlla @ 28.08.2013. 08:12 ] @
Imam jos jedno pitanje radim zadatak gde treba naci poslednju cifru broja 777^555^333.E sad znam da 7 i 3 su brojevi ciklicnosti 4 a 5 je ciklicnosti 1 odnosno njihovi stepeni.E sad posto mi je potrebna samo zadnja cifra negde sam procitao da mogu da posmatram samo poslednju sedmicu ali ne znam da li to isto mogu da uradim za stepene mada ce se 555^333 uvek zavrsavati na 5.E sad imam opciju da to sve napisem kao 7^5^3 sto je 7^125 sto je isto sto i 7^1 zbog ciklicnosti 4 stepena 7-ice ili da kazem da posto se 555^333 uvek zavrsava 5 da je poslednja cifra od 7^5 ista kao i 7^555^333.Da li ovo moze da se posmatra na ovakav nacin?
[ Nedeljko @ 28.08.2013. 08:42 ] @
Ojlerova teorema. Nađi ostatak svega pri delenju sa 10.
Najpre nađi ostatak od 555^333 pri delenju sa 6, pa onda sedmicu digni na toliko odbacujući umnoške od 10.
[ dovlla @ 28.08.2013. 09:48 ] @
Posmatrao kakve rezultate daje pri deljenju sa 6 poslednja cifru 5-ice na 333 i na parnim stepenima daje ostatatak 1 a na neparnim 5 pa ce na kraju biti ostatatak 5 pa predpostavljam da to isto daje i 555^333 pri deljenju sa 6.Dakle trazim ostatak pri deljenju 7^5 sa 10 a to je upravo 7.Je li dobro sad mada i ja dobijam isto resenje sa mojim postupkom gore.
[ kingW3 @ 28.08.2013. 11:05 ] @
Preko ojlerove teoreme možeš ovako,pošto 555^333 daje ostatak 3 pri deljenju sa 6 jer
555 mod 6=3
Sad gledaš za 3^333 ostatak pri deljenju sa 6
3^2=9 mod 6=3
Pošto je ostatak jednak 3 znači 3^3 mod 6=3^2 mod 6
Onda opet ide 3*3=9 mod 6=3 znači za svako 555^x mod 6=3
a 7^3=343 tj. završava se sa 3
Mada ja više volim ovaj način
poslednja cifra 7^x
je 7,9,3 ili 1
to se gleda po x mod 4,a za deljivost sa brojom 4 gledaš samo poslednje dve cifre tako da gledaš kako se 55^n menja 55*55=3025,
25*55=1375
75*55=4125
To znači da gledaš 333 mod 2 što je 1,znači završava se sa 75 a 75 mod 4 daje 3
znači poslednja cifra je 3
[Ovu poruku je menjao kingW3 dana 28.08.2013. u 12:22 GMT+1]
[ number42 @ 28.08.2013. 15:20 ] @
Citat: dovlla:
Imam jos jedno pitanje radim zadatak gde treba naci poslednju cifru broja 777^555^333.E sad znam da 7 i 3 su brojevi ciklicnosti 4
mislim da su ovo sasvim dovoljni podaci za resavanje.
kako je za 7 ciklicnost 4, onda (za 777^555) podelimo 555 sa 4, i ostatak je 3. a znamo da je treci u ciklusu od 4 trojka, tj to je zadnja cifra.
onda imamo .....3^333, ciklicnost je opet 4 (zbog trojke kao zadnje cifre osnove), podelimo 333 sa 4 i ostatak je jedan. a prvi u ciklusu od 4 je opet trojka, a to bi trebalo da je i resenje, znaci valjda 3.
[ Nedeljko @ 28.08.2013. 15:32 ] @
dovlla
Ovo što ti piše number42 nije tačno jer je 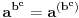 , a ne 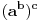 . To je tako jer je 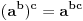 , pa nema potrebe za još jednom oznakom. [ dovlla @ 28.08.2013. 16:58 ] @
Znam.Posto treba prvo da se radi 555^333=x a onda 7^x.Zaboravio sam da pitam zasto trazim 555^333 mod6 zasto bas 6?Posto Ojlerova teorema kaze sa vikipedije a^p(n)=1 modn npr.ako trazimo zadnju cifru od 7^222 po mod 10.Kako su 7 i 10 uzajamno prosti tj.nzd(7,10)=1 to je uslov Ojlera i p(10)=4 a to je zapravo ona ciklicnost gde su p(10) brojevi 1,3,7,9 takvi da je npr.nzd(10,3)=1.Pa je sada 7^222=7^(4*45) * 7^2=49 mod 10=9 mod 10 pa je zadnja cifra 9.
[ number42 @ 28.08.2013. 17:11 ] @
Citat: treba prvo da se radi 555^333
@dovlla,
e to je vec drugi slucaj, sorry, za ovo ne znam kako ide.
al ako resavas na ovaj nacin kontam da ti je potrebna i predzadnja cifra (jer kod 5 ciklicnost je 1 pa je uvek zadnja 5), da bi taj broj mogao da podelis sa 4 i vidis redni broj u ciklusu.
pa verovatno ide neki drugi postupak.
[ number42 @ 28.08.2013. 17:32 ] @
cek bre, sad mi palo na pamet- ako je predzadnja cifra (za 555^xyz) uvek 2, to znaci da je ostatak pri deljenju sa 4 uvek 1, tako da je (kako je ciklus za sedmicu 4) ovo prvi broj u ciklusu, a on je 7.
tako da je resenje 7, ako je tacna ova pretpostavka o predzadnjoj cifri.
ako je tacno ovo logiciranje, onda je resenje u 2 reda, al ipak proveri.
[ kingW3 @ 28.08.2013. 20:19 ] @
number42 pogledaj moj post gore, 555^x se menja iz 25 u 75
Nisam siguran što mod 6 jer to nije ni broj phi(10),niti je uzajamno prost sa 555.Tu može mod 4 jer je to phi(10),a i 4 je uzajamno prosto sa 555(možda može i 6 nego ja znam samo zašto mod 4)
To je onda
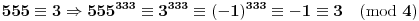
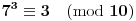 [ number42 @ 28.08.2013. 21:15 ] @
Citat: 555^x se menja iz 25 u 75
video sam da si ovo napisao, ali nisam bas skontao kako si ovo izveo i dobio ove rezultate?
ja dobijam suprotno, znaci recimo
5^2=25
25*25=...25
...25*...25=...25
itd. u opstem slucaju 555^x=...25
ne znam, mozda se moze i uopstiti na ...5^xyz=...25?
[ dovlla @ 28.08.2013. 21:20 ] @
Mislim da je kingW3 ovo dobro odradio.Trebalo bi da je dobro jer zaista 555 i 4 ali i 555 i 6 su uzajamno prosti pa moze da se radi i mod4 i mod6 jer oba zadovoljavaju uslove Ojlera.
[ number42 @ 28.08.2013. 23:14 ] @
Citat: kingW3:
number42 pogledaj moj post gore, 555^x se menja iz 25 u 75
da, bravo majstore, u pravu si.
mogao sam i ranije da koristim kalkulator, ono, bas je ocigledno. znaci, 555^x se menja od ....25 do ...75 zavisno da li je x parno ili neparno. kako je 333 neparno, znaci da zavrsava sa 75.
onda imamo 777^...75, a kako je ciklicnost sedmice cetvorka, onda ...75 delimo sa 4, i imamo ostatak 3. a ciklus od cetiri broja za sedmicu je 7, 9, 3, 1, a to znaci da je (kako je ostatak 3) treci broj trazeni rezultat, a to je 3.
nema greske stvarno, odmah si dao resenje koliko vidim. [ number42 @ 28.08.2013. 23:17 ] @
Citat: dovlla:
555 i 6 su uzajamno prosti
jesi li bas, ono 100% siguran? :)
[ dovlla @ 29.08.2013. 00:51 ] @
Izvini nisam video 6 i 555 nisu jer je 555 deljiv sa 3 kao i 6.Nisam proveravao moja greska.Znaci samo 4.
[ dovlla @ 29.08.2013. 08:59 ] @
Treba da odredim sve kompleksne brojeve z za koje vazi arg[z^3(1/2-isqrt(3)/2)]=-p/3,|z|^2+|z|-12=0.E sad preko Moavrove formule sam iz prvog izraza dobio da je z=|z|*(cos(-p/9)+isin(-p/9)) a iz druge nakon zamene |z|=t radim kao kvadratnu jednacinu i dobijam da je t=-4 i t=3 prvo odbacujem pa ostaje da je |z|=3 i zamenim ga u prvi izraz i konacno dobijam da je z=3*(cos(-p/9)+isin(-p/9)) ali ne znam da li moze da se radi na ovaj nacin.
[ darkosos @ 29.08.2013. 09:26 ] @
Mislim da ovo z=|z|*(cos(-p/9)+isin(-p/9)) nije dobro: koristeci arg(z1*z2) = arg(z1) + arg(z2) itd... trebalo bi da se dobije da je arg(z) = 0.
[ dovlla @ 29.08.2013. 09:49 ] @
Nisam mogao da se setim ove formule arg(z1*z2)=arg(z1)+arg(z2).Pa je jedino resenje z=3 jer z=|z|*(cos0+isin0)=|z| zbog arg(z)=0.Hvala.
[ Nedeljko @ 29.08.2013. 10:14 ] @
Pardon,
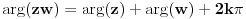 .
Treba da dobiješ tri rešenja. [ darkosos @ 29.08.2013. 10:39 ] @
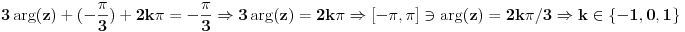 . [ dovlla @ 29.08.2013. 11:28 ] @
Ok.Sad mi je jasno.
[ dovlla @ 29.08.2013. 16:28 ] @
Ako polinom P(x) pri deljenju sa polinomom (x-a) daje ostatak ra, a pri deljenju polinomom (x-b) ostatak
rb, odrediti ostatak pri deljenju polinoma P(x) polinomom Q(x) = (x-a)(x-b).Znam da je P(a)=ra i P(b)=rb i kako x−y|p(x)−p(y) u Z[x,y] za p(x)∈Z[x] imam da a-b|P(a)-P(b)=ra-rb.P(x)-ra=(x-a)R gde je R∈N.Za x=b dobijam da je rb-ra=(b-a)R odakle dobijam da je R=(rb-ra)/(b-a).Pa je P(x)=(x-a)*(rb-ra)/(b-a)+ra.E sad treba da nadjem ostatak pri deljenju P(x) sa Q(x)=(x-a)(x-b) pa imam da je onda P(x)=W(x)(x-a)(x-b)+cx+d,gde je cx+d ostatak.Pa je sad P(a)=ra=ca+d odakle je c=0 jer je ra neka konstanta pa je ra=d=rb jer se slicno dobija za P(b).Ispada da je trazeni ostatak ra=rb.Ovo je sigurno neka greska?
[ Nedeljko @ 29.08.2013. 16:40 ] @
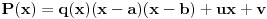 ,
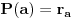 daje
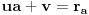 ,
dok 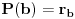 daje
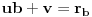 .
Rešimo ovaj sistem po  i  .
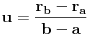 ,
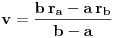 .
Dakle, ostatak je
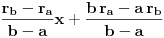 . [ dovlla @ 30.08.2013. 21:16 ] @
Ako je f(x)=x/sqrt(1+x^2) treba da dokazem da je f^n(x)=x/sqrt(1+nx^2) za svako n iz N,gde je f^n kompozicija f-ja f(x).Mislio sam da pokusam mat.indukcijom ali imam problema da dokazem i nemam ideju sta dalje da radim.
[ Sonec @ 30.08.2013. 21:31 ] @
[ dovlla @ 30.08.2013. 22:21 ] @
Izvini pogledacu za ovaj Latex.I ja sam tako radio ali pazi zar ne treba da dole bude sqrt(1+nx^2/(1+nx^2)) pa se na kraju dobija x/sqrt(1+2nx^2).
[Ovu poruku je menjao dovlla dana 30.08.2013. u 23:42 GMT+1]
[Ovu poruku je menjao dovlla dana 30.08.2013. u 23:44 GMT+1]
[ Sonec @ 30.08.2013. 22:46 ] @
Ne treba, jer ovde posmatras f-ju 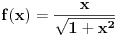 i kad zamenis  sa 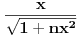 dobija se prikazano. Nema potrebe da se izvinjavas za  , to je samo bio predlog radi preglednosti. [ dovlla @ 30.08.2013. 23:42 ] @
Na koliko nacina se 20 bombona moze podeliti na cetiri devojcice tako da svaka dobije bar po jednu bombonu.Mislio sam da idem kombinacije ali se izraz previse komplikuje.Ima formula sa pocetka posta u vezi sa sestocifrenim brojevima P(n,k) ali nisam siguran da li nju mogu da primenim i na koji nacin.
[ Nedeljko @ 31.08.2013. 00:32 ] @
P(16,4)
[ dovlla @ 03.09.2013. 08:12 ] @
U skupu od 1000 tacaka ima tacno 10 cetvorki kolinearnih tacaka.Koliko je najvise razlicitih pravih odredjeno ovim skupom tacaka?Nemam ideju kako da odredim ove prave svaka pomoc je dobrodosla.
[ Nedeljko @ 03.09.2013. 12:19 ] @
Kada ne bi bilo trojki nekolinearnih tačaka, onda bi bilo
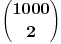 ,
pravih. Međutim, ovde treba izbaciti duplikate. Svaka od te dve četvorke određuje po jednu pravu i one određuju različite prave. Svaka od tih pravih se može odrediti pomoću bilo koje dve od te četiri tačke, to jest, na 6 načina. Kada bismo odbili sve te načine, izbacili bismo i te dve prave, pa ih treba dodati. Dakle, može biti najviše
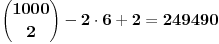
pravih. [ dovlla @ 03.09.2013. 16:05 ] @
Hvala.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|