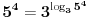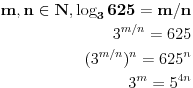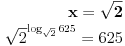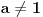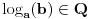[ number42 @ 31.08.2013. 15:43 ] @
| hteo sam da pitam da li dobijam jednakost ako celobrojne stepene transformisem u iracionalne? npr, imam 3^6+5^4 i to zelim da transformisem u neki izraz koji ce umesto tri i pet imati iste osnove, x^y+x^z. e sad ne znam koje brojeve dobijam kao x, y i z, ali me zanima ako su iracionalni da li je u tom slucaju taj izraz jednak pocetnom izrazu? nebitno konkretno za ovaj primer, ovo je samo ilustracija, zanima me u opstem slucaju. ili je priblizno jednak? |