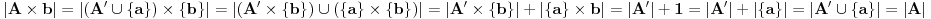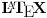Pogledaj kako je ovaj http://www.elitesecurity.org/t455962-0#3173997 zadatak uradjen, pa pokusaj sam da uradis svoj.

previse konfuzno i nelogicno objasnjenje da bi se interpretiralo djaku 5. razreda

Rešenje nije nimalo konfuzno, već zahteva da se neko udubi u njega i objašnjava kako se rade slični zadaci.

Što se nelogičnosti tičle, ne postoje više i manje logično/nelogično, već samo logično i nelogično. Ono je logično - nema nijedne greške.

E, sad, za one koji ne žele da se udube u rešenje nema rešenja. Bez muke nema nauke.

Ovakvi zadaci se zaista najlakše rešavaju Venovim dijagramom. Pokušaću da dam opis popunjavanja polja (dati tekst se čita unazad):

- u presek sva tri skupa stavi se 3
- u drugi deo preseka između skupova Literarnog i Matematičkog se upiše 1, jer već ima 3 a ukupno je 4
- u drugi deo preseka između skupova Likovnog i Matematičkog se upiše 5, jer već ima 3 a ukupno je 8
- na sličan način u drugi deo preseka Likovnog i Literarnog se upisuje 8 = 11-3

Koristeći ukupan broj za svaki konkurs se mogu upisati brojevi za ostatak polja.

Zbir svih ispisanih brojeva je ukupan broj učenika. Za ostalo se javi ako ima nejasnoća.

E da, ako je zadatak tačno urađen, sigurno je logičan :)

Pozdrav!

Imam nekoliko zadataka sa skupovima koje ne radim korektno. Treba da napisem i dokazem formule za princip sume, princip proizvoda i princip ukljucenja-iskljucenja. Ovo moze direktno sa slike da se iscita ali profesor ne priznaje resenja.

Napiši tačnu postavku.

Definisati princip sume, princip proizvoda i princip ukljucenja-iskljucenja za tri skupa. Kasnije je rekao da moramo i da dokazemo formule.

Koje formule?

Princip Sume
|A U B U C| = |A| + |B| + |C| ako preseci ova tri skupa prazan skup.

Princip Ukljucenja - Iskljucenja

|A U B U C| = (|A|+|B|+|C|) - (|A ∩ B| + |A ∩ C| + |B ∩ C|) + |A ∩ B ∩ C|

Princip proizvoda

|A x B x C| = |A|*|B|*|C|

Ako su A i B disjunktni i konačni, onda dokaz izvodimo indukcijom po |B|..

1. |B|=0.

Skup |B| je prazan pa se

|A U B| = |A| + |B|

svodi na

|A| = |A| + 0,

što je tačno.

2. |B|>0.

Izaberimo bilo koji element b skupa B i neka je B'=B-{b}. Po induktivnoj hipotezi je

|A U B'| = |A| + |B'|.

Takođe je

|A U B| = |A U (B' U {b})| = |(A U B') U {b}| = |A U B'| + |{b}| = |A| + |B'| + 1 = |A| + |B|.

Ovde je korišćena činjenica da b ne pripada skupu A U B'. Skupu A ne pripada jer pripada skupu B koji je disjunktan sa njim, a skupu B' po načinu njegovog izbora.

Kada to znamo, onda je

|A U B U C| = |A U B| + |C| = |A| + |B| + |C|.

Obzirom da je A disjunktna unija skupova A-B i A ∩ B, važi

|A| = |A-B| + |A ∩ B|.

Slično je

|B| = |B-A| + |A ∩ B|.

Sabiranjem ove dve jednakosti dobijamo da je

|A| + |B| = |A-B| + |B-A| + 2|A ∩ B|.

Obzirom da je A U B disjunktna unija skupova A-B, B-A i A ∩ B, važi

|A U B| = |A-B| + |B-A| + |A ∩ B|.

Oduzimajući ovu jednakost od prethodne, dobijamo da je

|A| + |B| - |A U B| = |A ∩ B|,

što je ekvivalentno sa

|A U B| = |A| + |B| - |A ∩ B|.

Kada to znamo, onda je

|A U B U C| = |A U B| + |C| - |(A U B) ∩ C| = |A| + |B| - |A ∩ B| + |C| - |(A ∩ C) U (B ∩ C)| = |A| + |B| + |C| - |A ∩ B| - (|A ∩ C| + |B ∩ C| - |(A ∩ C) ∩ (B ∩ C)|) = |A| + |B| + |C| - |A ∩ B| - |A ∩ C| - |B ∩ C| + |A ∩ B ∩ C|.

Dokaz da je |A x B| = |A|*|B| izvodimo indukcijom po |B|.

1. |B| = 0.

Skup B je prazan, pa je i skup A x B prazan, pa se jednakost |A x B| = |A|*|B| svodi na

0 = |A|*0.

2. |B|>0.

Neka je b proizvoljan element skupa B i B' = B-{b}.

|A x B| = |A x (B' U {b})| = |A x B'| + |A x {b}| = |A|*|B'| + |A| = |A|*(|B'| + 1) = |A|*(|B'| + |{b}|) = |A|*|B' U {b}| = |A|*|B|.

No, treba dokazati da je |A x {b}| = |A|. Dokaz izvodimo indukcijom po |A|.

1. |A| = 0.

Skup A je prazan, pa je prazan i skup |A x {b}|, pa se jednakost |A x {b}| = |A| svodi na

0 = 0.

1. |A|>0.

Neka je a proizvoljan element skupa A i A' = A-{a}.

|A x {b}| = |(A' U {a}) x {b}| = |(A' x {b}) U ({a} x {b})| = |A' x {b}| + |{a} x {b}| = |A'| + 1 = |A'| + |{a}| = |A' U {a}| = |A|.

Kada znamo da je |A x B| = |A|*|B|, onda je

|A x B x C| = |A x B|*|C| = |A|*|B|*|C|.

Hvala na odgovoru!

Potreban mi je jos dokaz za broj elemenata partitivnog skupa.

Ako je A konacan neprazan skup, onda je 2^A njegov partitivni skup (familija). Broj elemenata partitivnog skupa je
|2^A| = 2^n, gde |A| = n

U svesci imam sledece zapisano:

|A| = n, |2^A| = 2*|2^A1|

|2^A| = 2*2^(n-1) = 2^n

ali ne razumem ovaj dokaz pa ne znam da li je tacan.

Indukcijom po |A| na sličan način kao malopre.

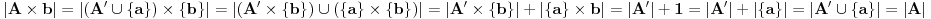
Ovo sam samo napisao da bih pokazao da je proradio na forumu (doduse, malo u drugacijem obliku, al bitno je da radi).

Probacu sutra da uradim pa cu ovde da postujem.