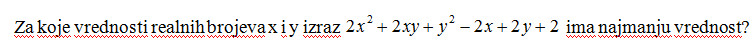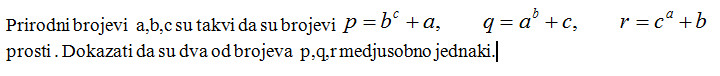Prvi se rešava preko parcijalnih izvoda.

izvod po x od ,
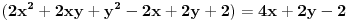
izvod po y od ,

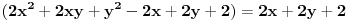
Izjednačavajući ih sa nulom dobijamo sistem

2x+y=1,
x+y=-1,

čije je rešenje x=2, y=-3.

Funkcija u toj tački ima vrednost 17.

Obzirom da je limes fiunkcije kada x i y teže beskonačnosti po apsolutnoj vrednosti, postoji neko R takvo da je za x²+y²>=R² ispunjeno da je funkcija u toj tački veća od 17. Na kompaktu x²+y²<=R² funkcija dostiže minimum, koji nije veći od 17 i samim tim to je minimum funkcije u celoj ravni. Taj minimum se ne dostići na rubu, nego u unutrašnjosti, pa parcijalni izvodi moraju biti jednaki nuli u njemu. No, postoji tačno jedna takva tačka.

U drugom treba posmatrati polinome

p(x)=(x+b₁)...(x+b₂₀₁₃)-lambda
q(x)=(x+a₁)...(x+a₂₀₁₃)+lambda

Uslov zadatka je da je

(1) p(a₁)=...=p(a₂₀₁₃)=0

i treba dokazati da je

(2) q(b₁)=...=q(b₂₀₁₃)=0.

Pošto su svi a_i različiti, ima ih onoliko koliki je stepen polinoma p i svi su mu koreni, oni su upravo svi koreni polinoma p, koji nema višestrukih korena. Na osnovu Vijetoih pravila je

a₁+...+a₂₀₁₃=-(b₁+...+b₂₀₁₃),
...
a₁...a₂₀₁₃=-(b₁...b₂₀₁₃-lambda).

Da bismo dokazali (2), obzirom da su svi b_i međusobno različiti i ima ih tačno onoliko koliki je stepen polinoma q, dokazivanje (2) se svodi na dokazivanje jednakosti

b₁+...+b₂₀₁₃=-(a₁+...+a₂₀₁₃),
...
b₁...b₂₀₁₃=-(a₁...a₂₀₁₃+lambda).

Poslednja jednakost se ne uklapa, što znači da je u zadatku trebal da stoji lambda umesto -lambda.

Ako su a i b parni, onda je p paran broj veći od 2, pa ne može biti prost. Ako su a i c parni, q ne može biti prost kao paran broj veći od 2, a ako su b i c parni, onda r ne može biti prost kao paran veći od 2.

Dakle, među brojevima a,b,c najviše jedna je paran, pa moraju postojati dva neparna. Pritom oba neparna broja moraju biti jednaka 1 jer je u suprotnom jedan od brojeva p, q, r paran veći od 2, pa nije prost. No, ako je a=b=1, onda je q=r. Ako je a=c=1, onda je p=r, a ako je b=c=1, onda je p=q.

U prvom zadatku funkcija teži beskonačnost kada x i y teže beskonačnosti po apsolutnoj vrednosti jer je jednaka

x²+(x+y)²-2(x+y)+2=
x²+(x+y-1)²+1.

Odavde se direktno vidi da se minimum dostiže u tački (0,1) i da izosi 1. Tačka u kojoj su parcijalni izvodi jendaki nuli je bila pogrešno izračunata.

Zar nije minimum u tački (2,-3)?Jer su tad parcijalni izvodi jednaki nula tj. rešenje sistema jednačina
2x+y=1
x+y=-1
A vrednost je -3,a ne 17.I da pošto se preko testa za drugi izvod dobija 4,a 4 je veće od 0 i izvod fxx je veći od 0 znači da je to minimum funkcije.



_{[Ovu poruku je menjao kingW3 dana 21.09.2013. u 15:32 GMT+1]}

Ne, to znači da je u pitanju lokalni minimum. Da bi dokazao da je u pitanju globalni minimum, potrebno je još obrazloženja.

Pogrešno sam prepisao funkciju. Dakle, ona glasi

x²+(x+y)²-2x+2y+2=
x²+(x+y)²-4x+2(x+y)+2=
(x-2)²-4+(x+y+1)²-1+2=
(x-2)²+(x+y+1)²-3.

Da, minimum se dostiže u tački (2,-3) i iznosi -3.

Hvala vam puno na pomoci!