Samo je glupo napisano. Integrališ 1/r po dx. U stvari trebalo bi da donja granica bude -(a+c) a gornja granica -c dx/x uzimajući u obzir orijentaciju x ose koja je nacrtana i uz pretpostavku da se provodnik sa strujom I1 nalazi u x=0.

Kada bolje razmislim, čini mi se da treba da bude u imeniocu logaritma c, a ne a.

I meni se cini da je tu stamparska greska. granice su od c do c + a. Zato je i stavio od 0 do a, mada je tako nepotrebno brljavo napisano.

Možete li ovo bolje obrazložiti, s obzirom da je djoka_l rekao da donja granica treba biti ? Još jednom hvala na pomoći svima.



Zar ne bi trebalo obratno?

_{[Ovu poruku je menjao R A V E N dana 09.10.2013. u 18:26 GMT+1]}

OK, da počnem od prve formule:




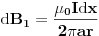
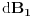
je magnetna indukcija dela trakastog provodnika širine dx na rastojanju r od beskonačnog linijskog provodnika. Da bismo dobili ukupnu indukciju, moramo sabrati doprinose svih ovih elementarnih linijskih provodnika.

Ako postavimo koordinatni sistem tako da je x osa u ravni crteža, i ide s leva u desno i ako postavimo da je centar koordinatnog sistema u tački gde beskonačni linijski provodnik sa strujom I1 prolazi kroz ravan crteža, tada je početak trakastog provodnika levo od koordinatnog početka na daljini a+c što u našem koordinatnom sistemu predstavlja tačku -(a+c) (minus znak je zato što je LEVO od koordinatnog početka). Kraj oblasti po kojoj radimo integraciju je na desnom kraju trakastog provodnika koji je na udaljenosti c od koordinatnog početka tj. na x osi ta tačka je -c.

Sa druge strane, r je funkcija od x. Uzmi neki dx na trakastom provodniku. Taj dx se nalazi na x osi na rastojanju r od koordinatnog početka i vrednost tog r je -x. Zašto -x - zato što je ceo provodnik na negativnom delu x ose i sve vrednosti x su na tom delu x ose negativne. Sa druge strane, vrednost r mora da bude pozitivna, a meri se od dx do koordinatnog početka (tj. do provodnika I1).

Sada nam integral posltaje



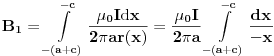
Dakle šta sam uradio: Izvukao sam ispred integrala ono što je konstantno, a r(x) (r koje je funkcija od x) sa zamenio vrednošću funkcije, što je -x.
Dalje, mogu da promenim znak kako ne bih radio sa -x, a tada moram da menjam i znak granice,kao i da zamenim donju i gornju granicu:



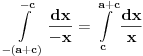
Ovo je tablični integral: integral 1/x je ln(x), sada je gornja granica (a+c), a donja c pa imamo:



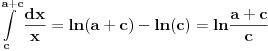
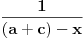
Da smo uzeli da je koordinatni početak na levoj strani trakastog provodnika, tada bi granice integrala bile 0 i a, a podintegralna funkcija bi bila i to zato što je početak koordinatnog sistema na rastojanju a+c od linijskog provodnika, a rastojanje r se SMANJUJE kako se ide u desno po širini trakastog provodnika.
I na ovaj način bismo dobili isti rezultat.