[ goxim69 @ 26.10.2013. 05:55 ] @
| pokazati da je relacija prazan skup na praznom skupu S refleksivna, simetricna i tranzitivna |
|
[ goxim69 @ 26.10.2013. 05:55 ] @
[ Nedeljko @ 26.10.2013. 09:00 ] @
[ goxim69 @ 28.10.2013. 18:43 ] @
Nedeljko da li moze malo pojasnjenje, ja mislim da je u ovom slucaju relacija ekvivalencije, odnosno da je refleksivna simetricna i tranzitivna.
Hvala unapred [ goxim69 @ 28.10.2013. 18:44 ] @
Nedeljko da li moze malo pojasnjenje, ja mislim da je u ovom slucaju relacija ekvivalencije, odnosno da je refleksivna simetricna i tranzitivna.
Hvala unapred [ Nedeljko @ 28.10.2013. 19:39 ] @
Prazna relacija jeste simetrična, antisimetrična i tranzitivna, ali na nepraznom domenu nije refleksivna.
[ goxim69 @ 30.10.2013. 05:56 ] @
Ali u ovom slucaju domen je prazan S={}
moje misljenje je da je u tom slucaju refleksivna, ako se nevaram [ Nedeljko @ 30.10.2013. 06:38 ] @
Ne vredi da ti odgovaram direktno. Pokušaj da primeniš ovo
Citat: Nedeljko: 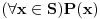 se definiše kao se definiše kao 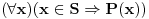 . .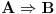 je netačno kada je je netačno kada je  tačno, a tačno, a  netačno. U ostalim slučajevima je netačno. U ostalim slučajevima je 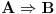 tačno. tačno.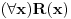 je tačno ako i samo ako je je tačno ako i samo ako je 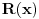 tačno za sve vrednosti tačno za sve vrednosti  . .Iz ovih definicija izvedi da je 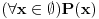 tačno, bez obzira na to šta je tačno, bez obzira na to šta je  . .U poslednjem redu je bila greška. Umesto "netačno" je trebalo da stoji "tačno", što sam ispravio u citatu. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|