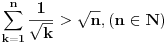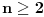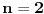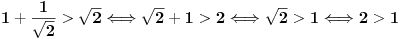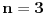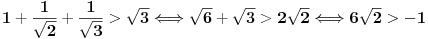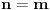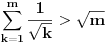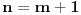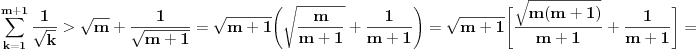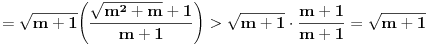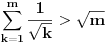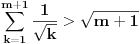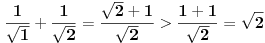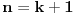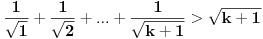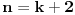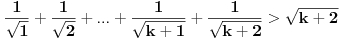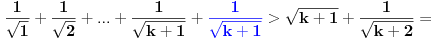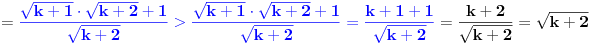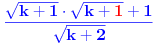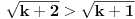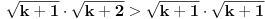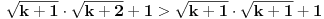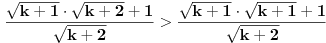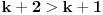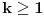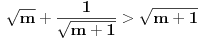[ R A V E N @ 26.10.2013. 12:08 ] @
|
| Prvo navodim cijeli zadatak iz zbirke:
Dokazati da nejednakost:
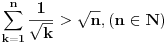 (*) (*)
vrijedi za svaki prirodan broj 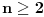 . .
Dokaz. Za 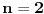 dobijamo da je: dobijamo da je:
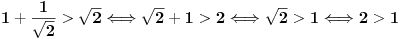 . .
Za 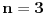 uslov je takođe ispunjen, tj. uslov je takođe ispunjen, tj.
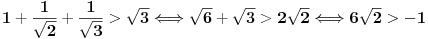 . .
Pretpostavimo da nejednakost (*) vrijedi za 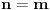 , tj. da je: , tj. da je:
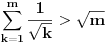 . .
Ako dokažemo da relacija (*) vrijedi za 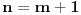 , onda će ona da vrijedi i za svaki prirodni broj , onda će ona da vrijedi i za svaki prirodni broj  . Zaista, . Zaista,
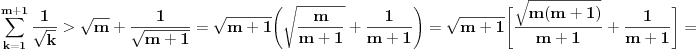
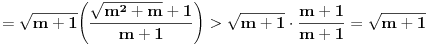 . .
Prema tome, ako je 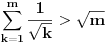 , onda je tim prije i , onda je tim prije i 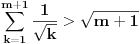 , što znači da je metodom matematičke indukcije izveden dokaz. , što znači da je metodom matematičke indukcije izveden dokaz.
Napomena: Dokaz smo mogli i ovako provesti:
1)Za 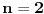 imamo: imamo:
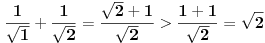 . .
2)Pretpostavimo da je za 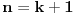 relacija ispunjena, tj.: relacija ispunjena, tj.:
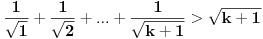 . .
Dokažimo valjanost tvrdnje i za 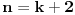 , tj. da vrijedi: , tj. da vrijedi:
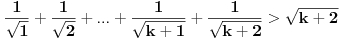 . .
Zaista,
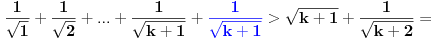
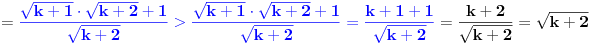 . .
Ovim je dokaz završen.
Kraj citata.
Meni nije jasno odkuda ovo što sam označio plavom bojom. Je li u pitanju neka krupna štamparska greška ili je meni nešto promaklo? Ako je ovo označeno plavom bojom nepravilno, kako treba pravilno?
[Ovu poruku je menjao R A V E N dana 26.10.2013. u 13:22 GMT+1] |
[ Sonec @ 26.10.2013. 14:06 ] @
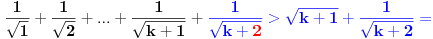
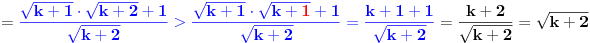
.
Da li treba neko dodatno objasnjenje?
Inace vazi:
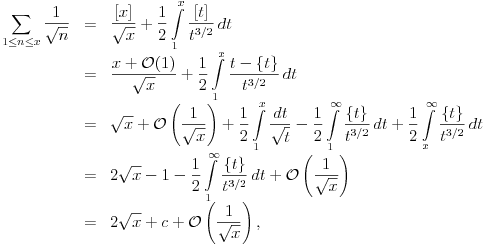
gde je
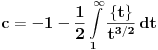
neka apsolutna realna konstanta.
U prvoj jednakosti koristili smo
Abel's summation formula za
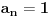
i
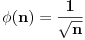
.

predstalja funckiju ceo deo, a
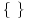
funckiju razlomljeni deo.
[ R A V E N @ 26.10.2013. 15:29 ] @
Hvala ti, Sonec, samo mi nije jasno odakle potiče ovo
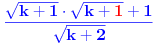
?
[ Sonec @ 26.10.2013. 16:21 ] @
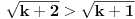
, pa je i
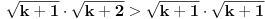
, tj.
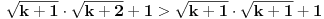
, a samim tim i
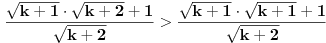
. E sad, zasto bas tako? Pa stelovanje, nista vise.
[ R A V E N @ 26.10.2013. 20:50 ] @
Na osnovu čega uzimaš
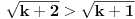
? Ne mogu to da izmoždim...

[ Sonec @ 26.10.2013. 22:03 ] @
Pa
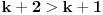
(
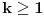
), pa ova relacija vazi i za korene (jer su potkorene velicine vece od 1, pa se ne menja znak nejednakosti).
[ miki069 @ 28.10.2013. 15:11 ] @
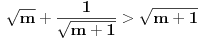
Ova nejednakost se dokazuje množenjem sa imeniocem i trivijalna je.
Ne razumem šta su petljali u toj knjizi.
[ R A V E N @ 28.10.2013. 15:36 ] @
Ovaj se zadatak pojavljuje i u knjizi Pavle Miličić, Momčilo Ušćumlić - Zbirka zadataka iz više matematike I, XX izdanje pod brojem 344., a i u ovoj mojoj "žutoj zbirci" je naveden dva puta.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
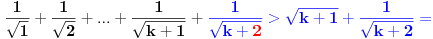
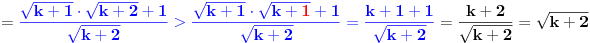 .
.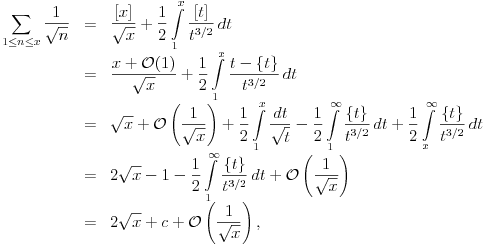
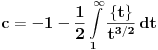 neka apsolutna realna konstanta.
neka apsolutna realna konstanta.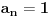 i
i 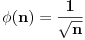 .
. predstalja funckiju ceo deo, a
predstalja funckiju ceo deo, a 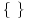 funckiju razlomljeni deo.
funckiju razlomljeni deo.