Sta fali dokazu teoreme iz Gojkove knjige:

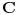
Teorema. Polje je algebarski zatvoreno. I uopste, ako neko polje karakteristike nula nema pravih rasirenja neparnog stepena, njegovo kvadratno rasirenje je i algebarski zatvoreno, ako i samo ako nema rasirenja stepena dva.

U dokazu se koristi teorija Galua i prva Silovljeva teorema.

Iskreno, nisam se nesto udubljivao u tvoj post, to diranje mecke me nikada nije puno zanimalo iskreno, al koliko vidim, za ovaj dokaz koji sam spomenuo se koriste obe aksiome koje si naveo.

Ma, ne fali mu ništa, samo što nije potpuno algebarski jer se poziva na 1 i 2, što prethodno izvodi nealgebarski iz aksiome supremuma.

Nije poenta problema u "algebarskoj čistoći", već u tome da li iz aksioma uređenog polja i jedne od aksioma 1 i 2 sledi da je kvadratno raširenje svakog takvog polja algebarski zatvoreno ili ne sledi?

Mislim da ne moze. To ovako intuitivno. Al ne bih umeo da pokazem.

Odgovor je tačan. No, da vidimo hoće li se javiti još neko.

Moguće da nešto propuštam, ali zar nije prilično jednostavno? Čini mi se da je dovoljno krenuti od polja i ubaciti još „nešto“ unutra na taj način da se u jednoj odnosno drugoj varijanti dobije polje koje zadovoljava prvu predloženu aksiomu odnosno drugu predloženu aksiomu, a ne zadovoljava traženi zaključak. Pritom meni deluje prilično očigledno šta je to „nešto“ što ćemo ubaciti u prvom, odnosno drugom slučaju (no ne isključujem mogućnost greške). Zasad neću eksplicitno da napišem u slučaju da neko želi da razmisli još malo.

Da, treba naći dva uređena polja čija algebarska zatvorenja nisu njihova kvadratna proširenja, pri čemu prvo treba da zadovolji prvu aksiomu, a drugo drugu.

Ima li zainteresovanih?