[ MajorFatal @ 09.11.2013. 00:57 ] @
...koja je kolicina (broj) simbola potrebna za predstavljanje nekog broja u razlicitim brojnim sistemima? Npr . za unarni to bi bilo za svaki novi broj na brojnoj pravi po 1 simbol vise tako da ako bi hteli to graficki da predstavimo to bi bilo nesto kao y=x samo bez nule tj. ako bi na x osi bila brojna (brojevna?) prava a na y osi broj simbola potreban za predstavljanje tih brojeva kako bi ta funkcija ako postoji izgledala za binarni i decimalni sistem?

Hvala unapred!
[ darkosos @ 09.11.2013. 08:38 ] @
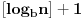
c = , gde je c broj cifara, b osnova brojnog sistema, n broj kome odredjujes broj cifara. Uglaste zagrada [] znace ceo deo, odnosno odbacivanje svega posle decimalnog zareza.
[ MajorFatal @ 09.11.2013. 13:21 ] @
Hvala! A oni nepozicioni (repetativni) i bez baze tipa rimljanski ili kombinovani kao majanski, kako za njih racunati broj upotrebljenih cifara, da li moze da se izrazi nekom funkcijom?
[ darkosos @ 10.11.2013. 14:51 ] @
Za rimske ne znam da li moze da se nadje neka jednostavna funkcija, ali ovako na prvu loptu, zavisi od broja jedinica, desetica, stotina, hiljada:
0: 0
1: 1
2: 2
3: 3
4: 2
5: 1
6: 2
7: 3
8: 4
9: 2

Npr 2814. Za 2 hiljade treba 2 cifre, za 8 stotina treba 4 cifre, za 1 deseticu treba 1 cifra i za 4 jedinice treba 2 cifre, ukupno 9 cifara: MMDCCCXIV.
[ MajorFatal @ 14.12.2013. 01:36 ] @
Dobro, nema formule, majanski je nesto kao: cifre su vredfnosti: 1, 5, 360, 7200, 144000,... tj. 1 pa 5 repetativno (ako upotrebljavam dobar izraz) tj 1. je predstavljeno jednom tackom pa 2, 3, 4 tacke, pa 5 tacaka zamenjuje 1 crtica itd... 360 (jer im je bilo potrebno za broj dana u godini) je konstruisano kao 18*20 i svaka sledeca cifra kao prethodna *20, 7200 = 360 *20, 144000 = 7200 * 20 itd... ima jos cifara koje su predstavljene nekim simbolima, kao neke glavuce sa isplazenim jezicinama, meni bi od pomoci bio i bilo kakav graficki prikaz jer, crtam vec danima, razvlacim onu x osu kao zvaku i skupljam ali nikako da svih 5 sistema zapakujem na 1 crtez, jos bi mi bilo zanimljivo i faktorski al da ne bi ispalo kao da narucujem...

Ne mogu da ne primetim da ovi repetativni sa svakom novom cifrom broj simbola potreban za opisivanje vrednosti nekog broja im pada na 1, tipa majanski vec kod pete cifre dolazi do 144000, sto se predstavlja sa 1 glavudzom sa isplazenom jezicinom pa...

verovatno je tupavo pitanje ali... ako bih hteo da predstavim neke jako velike brojeve, tipa koji bi u decimelnom brojnom sistemu zauzimali po nekoliko desetina stranica a4 formata ispisane decimalnim ciframa, mogu da racionalizujem tako sto povecam bazu pozicionog sistema, ali da li bih mogao da kombinujem sa repetativnim tipa od 65536 pola da uzmem za repetativne cifre a pola za pozicione, dobio bih pozicioni sistem sa osnovom oko 32000, plus 32000 repetativnih cifara

U stvari veoma je glupo pitanje, al svejedno ja da pitam, mozda neko nesto odgovori, napise