[ kingW3 @ 21.01.2014. 18:47 ] @
Počeo sam da vežbam za takmičenje i ne znam kako da uradim zadatak sa državnog takmičenja iz 2013(1 razred)

5.Dato je 6 tačaka u ravni. Neka je p broj različitih pravih koje
određuju parovi ovih tačaka. Koje sve vrednosti može imati p?

Znam samo da može da bude ,i dobio sam da su rešenja 5+4+3+2+1,4+3+2+1,3+2+1,2+1,1?Ili možda 15,10,9,6,1
Ako bi neko mogao da mi pokaže neki način da uradim ovaj zadatak bio bih veoma zahvalan

I ako nekome nije teško da pogleda da li sam ovaj zadatak ispod tačno uradio(na sajtu nemaju rešenja)
(2012)
5.Šest mudraca je govorilo o broju zapisanom u dekadnom zapisu.
Prvi: ,,Broj n umanjen za 1 je prost broj akko n ima bar jedan prost
delilac iz 1. desetice.”
Drugi: ,,Broj n je deljiv sa 2 akko n nije palindrom koji ima broj
cifara deljiv sa 2.”
Trći: ,,Broj n nije deljiv sa 3 akko ima manje od 3 neparna delioca.”
Četvrti: ,,Broj n je deljiv sa 4 akko ima tačno 4 cifre.”
Peti: ,,Broj n nije deljiv sa 5 akko je zbir cifara broja n jednak 5.”
Šesti: ,,Broj n nije uzajamno prost sa 6 akko ima tačno 6 delilaca.”
Odredite sve moguće prirodne brojeve n, ako se zna da je izjava svakog
mudraca tačna.
(Broj n je palindrom ukoliko je jednak broju koji se dobija čitanjem
broja n sa leva na desno. Npr. broj 1245421 je palindrom.)

Počeo sam tako što sam od trećeg mudraca zaključio da je,tako što da bi broj imao manje od 3 neparna delioca može da ima najviše jedan prost delioc,i može da ima neki stepen broja 2
p je prost broj
Ako je n deljivo sa 3,po šestom mudracu
3^5 nije zbog prvog mudraca,isto po prvom ako je p neparan n-1 je paran tj. nije prost,znači tj. i a po petom mudracu to nisu rešenja.
Znači n=p*2^k
Po 6om mudracu tj.
Po 2om mudracu n je palindrom koji ima broj cifara deljiv sa 2,pošto je n palindrom sa parnim brojem cifara on mora da je deljiv sa 11(ne znam kako bi ovo dokazao),znači a to nije po petom mudracu



[Ovu poruku je menjao kingW3 dana 21.01.2014. u 20:02 GMT+1]

[Ovu poruku je menjao kingW3 dana 21.01.2014. u 20:31 GMT+1]
[ djoka_l @ 21.01.2014. 20:56 ] @
Drugi zadatak si potpuno pogrešno počeo da rešavaš. Sve izjave mudraca predstavljaju logičke ekvivalencije.
Dakle izjava k-tog mudraca je oblika:



pa je taj iskaz tačan ako su oba tačna ili oba netačna tj:



Ti si ispitivao samo desnu stranu gornjeg logičkog izraza, a ne i levu stranu.
[ kingW3 @ 21.01.2014. 21:32 ] @
Verovatno sam loše napisao to,jer sam radio po slučejima uzimao npr. da je ,isto p je prost broj svugde u rešenju.Počeo sam tako što sam rekao da broj ili ima manje od 3 delioca ili je oblika 3t,ako je oblika 3t onda nije uzajamno prost sa 6 tako da ima 6 delioca.6 delioca imaju brojevi 3^5,3*p^2,p*3^2 Pošto je 3 u prvoj desetici n-1 mora da bude prost.A za ova dva poslednja slučaja to je moguće jedino ako je p=2,pošto to nisu rešenja znači da broj nije oblika 3t tj. da ima manje od 3 neparna delioca što je ekvivalento n=p*2^k,ovde sam napravio grešku jer p*2^k može da ima 6 delioca,kada je k=2,uslov je i da ima 4 cifre zato što je deljiv sa 4.Ako uzmemo da broj nije deljiv sa 5 to mogu da budu brojevi 1004,1112,a pošto su deljivi sa dva imaju delilac iz prve desetice,to povlači da 1003 i 1111 moraju da budu prosti,1111 je deljiv sa 11,1003 je deljivo sa 17 tako da ovo nisu rešenja.Kada bi n bio deljiv sa 5 imao bi više od 6 delioca ili ne bi imao 4 cifre.Znači n je uzajamno prosto sa 6,što povlači k=0
tj. n=p
A pošto broj nije deljiv sa 2 jer je p neparan prost broj,znači da je n palindrom sa parnim brojem cifara.
Ja barem mislim,ako te ne mrzi i ako sam nešto pogrešio napiši šta sam pogrešio.
Hvala unapred
[ Nedeljko @ 22.01.2014. 00:30 ] @
1. Pretpostavimo da je neparan broj veći od 3. U tom slučaju nije prost kao paran veći od dva, pa po prvoj izjavi nije deljiv ni sa jednim brojem od 2,3,5 i 7. Po drugoj izjavi je u tom slučaju palindrom sa parnim brojem cifara i samim tim deljiv sa 11. Obzirom da nije deljiv sa 3, po trećoj izjavi ima manje od tri neparna delioca, pa pošto parnih nema, mora biti prost. Obzirom da je deljiv a 11, mora biti jednak 11. Međutim, broj 11 se ne uklapa u petu izjavu. Stoga zamišljeni broj nije neparan veći od 3.

2. Brojevi 1 i 3 se ne uklapaju u drugu izjavu. Dakle, broj je paran.

3. Obzirom da je paran, po šestoj izjavi ima tačno šest delilaca. Ako bi bio deljiv samo jednim prostim brojem, onda taj prost broj ne sme biti neparan. Stepeni dvojke veći od 32 imaju više od šest delilaca, a manji od 32 imaju manje od šest delilaca, pa je broj jednak 32. Međutim, on se ne uklapa u četvrtu izjavu. Stoga broj ima bar dva prosta delioca. Ako bi ih imao bar tri, recimo p,q i r, onda bi imao bar osam delilaca - 1,p,q,r,pq,pr,qr i pqr, a ima ih tačno šest. Stoga, on ima dva prosta delioca, i štaviše jednak je proizvodu jednog od njih i kvadratu drugog, pri čemu jedan od njih mora biti 2.

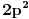
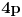
Ostala su dva slučaja, da je oblika ili , gde je neparan prost broj.

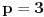
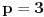
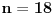
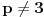
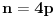
Po trećoj izjavi, akko je broj prvog od oblika, tj. akko je . Međutim, broj 18 se ne uklapa u petu izjavu, pa zaključujemo da je i da je . U tom slučaju, po četvrtoj izjavi broj ima tačno četiri cifre.

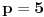
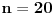
Ako je , onda je , a broj 20 nema tačno 4 cifre. Dakle, broj nije deljiv sa 5, pa mu je zbir cifara jednak 5.

Pošto je deljiv sa 4, poslednje dve cifre čine broj deljiv sa 4. Dakle, kandidati su

1400
4100
1004
1040
1112
2012
1220
2120

Delenjem sa 4 dobijaju se vrednosti za p

350
1025
251
260
278
503
305
540

Osim eventualno 251 i 503, za ostale se lako vidi da su složeni. Za ta dva se lako vidi da su prosti delenjem sa prostim brojevima manjim od njihovog kvadratnog korena. Dakle, treba ispitati da li se brojevi 1004 i 2012 uklapaju u prvu rečenicu.

1003 je deljiv sa 17, ali 1004 ima proste delioce manje od 10. Dakle, 1004 otpada.

2011 je prost i 2012 ima proste delioce manje od 10.


Dakle, jedini takav broj je 2012.
[ kingW3 @ 26.01.2014. 19:23 ] @
Hvala,nego jel zna neko kada i gde izlaze rezultati opštinskog takmičenja za B kategoriju(u Beogradu)?