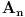
Neka je skup svih podskupova skupa koji nemaju susednih elemenata.

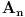
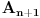
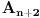
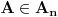
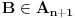
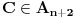
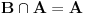
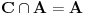
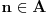
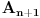
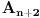
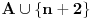
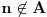
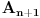
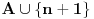
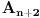
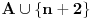
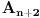
Svaki element bilo skupa pripada skupovima i . Za svaki skup napišimo sve skupove i takve da je i . Ako , onda je jedini element skupa koji u preseku sa skupom daje skup , dok u skupu postoji još jedan takav skup - . U slučaju kada onda su elementi skupa koji u preseku sa skupom daju skup zapravo i , dok u skupu postoji još jedan takav skup - . Dakle, u svakom slučaju u skupu imamo po jedan takav element više nego u skupu .

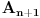
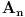
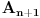
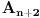
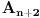
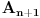
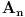
Kada to učinimo za sve elemente skupa , nabrojali smo sve elemente skupova i po jedanput. Međutim, elemenata skupa ima više od elemenata skupa i to tačno onoliko koliko ima elemenata skupa . Dakle,

.
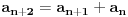