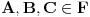
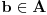
Neka . Za ma koje važi

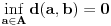
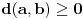
, jer je uvek , a sa druge strane je ,
.

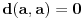
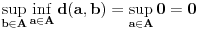
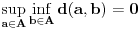
Na sličan način se zaključuje da je . Dakle,

.

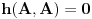
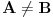
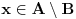
Ukoliko je , onda postoji ili .

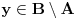
U prvom slučaju, pošto je skup zatvoren, postoji takvo da u okolini tačke nema tačaka skupa . Stoga je

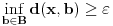
, jer je .
.

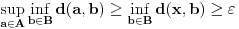
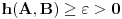
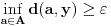
Odatle sledi da je . Na sličan način se radi i drugi slučaj, samo treba krenuti od za takvo da u okolini tačke nema tačaka skupa .

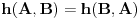
je očigledno.

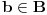
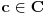
Ostala je nejednakost trougla. Za ma koje , i važi

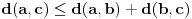
, (nejednakost trougla za )
,
, (na osnovu prethodnog i tranzitivnosti nejednakosti),
,
.
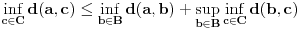
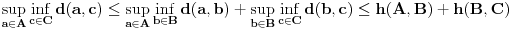
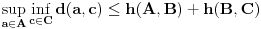
, (na osnovu prethodnog i tranzitivnosti nejednakosti)

Na sličan način se dokazuje i

.

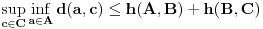
Odatle sledi da je

.
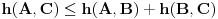