Rešenje je u prilogu.

Vau. I sve vreme mi ne pada na pamet da obrnem taj negativni eksponent.

Hvala puno!

Vidiš da sam i ja žvrljao deo smene koju sam probao dok nisam obrnuo taj negativan eksponent.
Iako nije promenjena vrednost razlomka, promenjena je struktura brojioca i imenioca.

Postoji i obrnuta situacija kod homogenih DJ.
Pravilo da se sa Z ništa ne krati dok se ne proba smena. Ako neće smena, onda tek kratiti, kao u ovom primeru.
Može se desiti da može smena pre kraćenja, a da ne može posle kraćenja.
Dakle pravilo je: "u toku sređivanja X kratiti, a Z nikako dok se ne vidi krajnji integral po Z".
Da ti ne navodim primer, naletećeš na takav zadatak sigurno.

Uvek pre rada kao homogena pogledaj da nije slučajno DJ u obliku totalnog diferencijala.
Mnogo brže se uradi kao totalni difrencijal, nego kao homogena.
Mnogo ima primera DJ da je i homogena i DJ u totalnom diferencijalu.
Ova nije bila u totalnom diferencijalu.


Nema na čemu.

Ne vredi, ovu sam danima pokušavala da rešim.
Ima li rešenja uopšte ili je neka brljotina?

http://imageshack.com/a/img834/92/uc62.jpg

Koliko ja vidim, ovo je jednacina totalnog diferencijala.

&5*#4$77&&$% 5& ""!%&&/(!!!!!!

Zahvaljujem.

Jednostavno nije ispao totalni kad sam proverila u par sekundi pa sam otpisala u startu i provela dva dana rešavajući pogrešno.

Jeste DJ u totalnom diferencijalu, ali je ujedno i homogena DJ.
Lakše se uradi kao TD nego kao HDJ (da ne ponavljam).

Nije nikakva muka da se uradi i kao HDJ (rešenje u prilogu).


C=1, a ne C=0. Greška u škrabanju.

Niti mi je ova smena pala na pamet :(

Nije toliko bitna ta smena.
Bitno je da nisi lutala oko vrste DJ i da je jasno da je homogena.
Ujedno i DJ u TD.

Koji je fakultet u pitanju?

Građevinski.
Ja sam davno polagala matematike i sad treba da se vratim tome posle nekoliko godina, pa nije baš lako :(

Opet ja :)

Da vas ne gnjavim previše, ispod je delimično rešen zadatak;

http://imageshack.com/a/img593/7087/tpue.jpg

koji, koliko god prevrtala, ne mogu da dovedem do njihovog rešenja, jer ne mogu da poništim x-1 na kom je već stepenu...

Znate li kako to rade?

Pozdrav i hvala još jednom.

Jedinu grešku koju sam video je zaboravljenja četvorka u prevođenju u faktorski oblik:

Piše: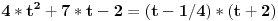


Treba: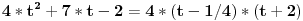


To menja krajnje rešenje, koje nisi ni napisala.
Ispravi i trebalo bi da se uklapa.


Evo ti malo urađenih primera:
http://www.puskice.org/downloa...3%20zbirka%20by%20Hijavata.pdf
Sa FON-a su zadaci.
Nije baš nešta ekstra, ali pomaže.
Ne sviđa mi se što linearnu DJ I reda rešava po formuli, a ne peške smenom y=u*v.

Jedna od boljih knjiga je od Dr Dušana Belajčića sa arhitekture.
Zove se DIFERENCIJALNE JEDNAČINE.
Mnogo dobro je objašnjeno i ima dosta urađenih primera.



_{[Ovu poruku je menjao miki069 dana 21.03.2014. u 00:05 GMT+1]}

Nisam napisala jer nije bilo tačno!
Sada jeste. Mnogo glupe propuste pravim.

Hvala i za knjigu, biće vrlo korisna :)

Ima li neko ideju, vrtim se u krug? Traži se partikularno.

http://imageshack.com/a/img856/8628/qr4j.jpg

Bio je pogrešan zadatak :(

_{[Ovu poruku je menjao Kaljava dana 31.03.2014. u 19:12 GMT+1]}

Evo male pomoci: posto je ovo jednacina oblika uvedi smenu , gde je . Tada je i nasa jednacina se svodi na .

Tnx, ali znam za smenu :)

Problem imam upravo sa jednačinom koja ostaje, tj.

z'(y) = z(y) - y + 1

Izgleda jednostavno ali šta god da joj uradim ne rešava se. Dobijam neki grozni koren i ne znam koja je smena :I
Stavila sam i potkorenu veličinu i deo potkorene veličine i menjala za kvadrat sa druge strane i ceo koren u smenu (ovo je još najviše obećavalo) ali ne ide.

Mnogo komplikujes. Ovo je linearna jednacina I reda (, sad je lakse cenim) i verujem da znas kako se ona resava. Verovatno te je bunilo sto imas , al ako ti je lakse, ti pisi (al to samo da bi je resila, a posle vrati na svoj slucaj).

Uradi se ova linearna po Z(y), ali ne može do kraja da se reši po y.

Dobija se:
Z(y) = y + C*e^y

Posle je po y nerešiv integral.

I to je dobro znati.

Hvala!