Skup sadrži sve racionalne brojeve jer je presek familije skupova od kojih svaki sadrži sve racionalne brojeve.
Skup je Borelov mere nula jer je

.

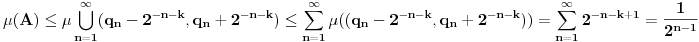
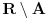
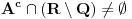
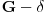
Stoga je skup pravi podskup od , pa pošto mu pripadaju svi racionalni brojevi, bilo koji element iz iracionalan broj, pa je . Štaviše, skup je svuda gust, jer sadrži sve racionalne brojeve. Kao skup ne može biti svuda gust i prebrojiv po Berovoj teoremi o kategorijama, pa je neprebrojiv, pa pošto je skup racionalnih brojeva prebrojiv, u skupu ima iracionalnih brojeva, pa je .

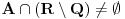
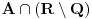
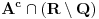
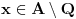
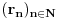
Skupovi i zavise od izbora numeracije racionalnih brojeva. Zaista, neka . Nađimo numeraciju racionalnih brojeva takvu da za skup



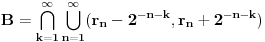
važi .

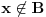
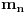
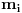
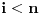
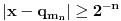
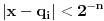
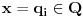
Neka je najmanji prirodan broj koji se razlikuje od za sve i takav da je . U tom nizu na osnovu konstrukcije nema ponavljanja prirodnih brojeva, a svi prirodni brojevi će se naći u njemu jer bi u protivnom postojao najmanji prirodan broj koji nije u tom nizu. Pošto svi manji prirodni brojevi jesu u nizu, zaključujemo da je za svako , odnosno da je , što je isključeno jer je broj iracionalan na osnovu izbora.

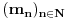
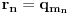
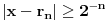
Dakle, niz , je permutacija skupa prirodnih brojeva, pa je jedna numeracija racionalnih brojeva za koju važi za svako , pa samim tim i

.

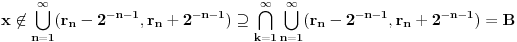
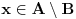
Dakle, , pa je .

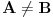
Poslednji deo zadatka se može rešiti simuliranjem dokaza korišćenog stava teorije mere i dokaza Berove teoreme o kategorijama.

Nedeljko, hvala Vam puno, mi još uvijek nismo učili Beorvu teoremu o kategorijama, upravo je pokušavam naći na internetu..