[ Cveks_87 @ 22.05.2014. 13:24 ] @
| Pre svega nisam znao kako da odkucam zadatke pa sam koristio tag [img][/img] i izvinjavam se zbog toga ako sam narusio neko pravilo... a evo i 2 zadatka koja ne umem da resim... Prvi zadatak:  Drugi zadatak:  |
|
[ Cveks_87 @ 22.05.2014. 13:24 ] @
[ Sonec @ 22.05.2014. 15:08 ] @
[ miki069 @ 22.05.2014. 16:00 ] @
Drugi može i indukcijom.
Baza indukcije je n=1, ali sam namerno radio za n=2. Na kraju uradiš samo sve slučajeve x veće/manje/jednako od y. Proizvod je uvek veći ili jednak 0. [ Cveks_87 @ 22.05.2014. 17:33 ] @
Hvala puno na resenju!!!
[ miki069 @ 22.05.2014. 20:32 ] @
U prvom valjda pokušavaš da namestiš:
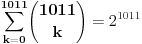 a ne 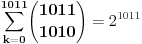 Ili sam ja nešta propustio? Zadatak pokušavam da uradim na nivou kombinatorike, ali mi se ništa ne "javlja". Koji je fakultet, odnosno nivo ispita? Čisto da bih znao šta je dozvoljeno od naprednijih alata. PS: Ovaj editor (LaTex) ćeš najlakše naučiti (ili bar upotrebiti) kopiranjem i editovanjem već napisanih komentara. [Ovu poruku je menjao miki069 dana 22.05.2014. u 21:48 GMT+1] [ Cveks_87 @ 22.05.2014. 21:30 ] @
[ Sonec @ 22.05.2014. 22:54 ] @
Prvi zadatak je koska. Primetimo da
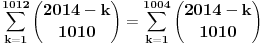 , jer su inace binomni koeficijenti jednaki nuli (ja sam uzeo tu definiciju koju sam nasao na netu, al obicno sam se pre susretao sa zadacima gde je sve bilo definisano na pocetku). Sad iskoristimo poznati identitet , jer su inace binomni koeficijenti jednaki nuli (ja sam uzeo tu definiciju koju sam nasao na netu, al obicno sam se pre susretao sa zadacima gde je sve bilo definisano na pocetku). Sad iskoristimo poznati identitet 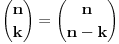 i problem se svodi na i problem se svodi na 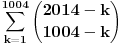 . Zato cemo se pozabaviti odredjivanjem sume . Zato cemo se pozabaviti odredjivanjem sume 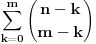 . Jedan od nacina bi bio taj da produzimo sumu za . Jedan od nacina bi bio taj da produzimo sumu za  kada su binomni koeficijenti jednaki nuli i uradimo sledece kada su binomni koeficijenti jednaki nuli i uradimo sledece 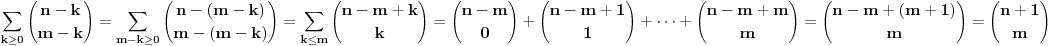 , gde smo koristili na kraju Paskalov identitet , gde smo koristili na kraju Paskalov identitet 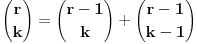 , pa su se clanovi u sumi medjusobno skratili. Dakle, nasli smo da je , pa su se clanovi u sumi medjusobno skratili. Dakle, nasli smo da je 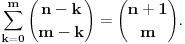 Vratimo se sad na nas problem. Primenom ove formule dobijamo da je Vratimo se sad na nas problem. Primenom ove formule dobijamo da je 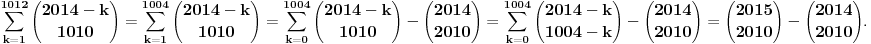 [ miki069 @ 23.05.2014. 06:39 ] @
Ne vidim grešku, ali je rezultat mnogo mali da bi bilo tačno.
[ Sonec @ 23.05.2014. 09:29 ] @
Jedinu gresku koju sam ja primetio je ta sto nisam dobijenu formulu primenio kako treba. Na kraju se dobija
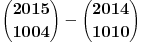 , odnosno, radi lepseg zapisa, , odnosno, radi lepseg zapisa, 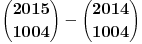 . Dakle, ne . Dakle, ne 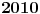 , vec , vec 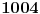 , odsnosno , odsnosno 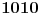 (mada je to isto kao i (mada je to isto kao i 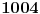 u tom binomnom koeficijentu). Ne znam na kojim sam drogama bio kada sam ovo pisao. Wolfram potvrdjuje ovo resenje link. u tom binomnom koeficijentu). Ne znam na kojim sam drogama bio kada sam ovo pisao. Wolfram potvrdjuje ovo resenje link.[ miki069 @ 23.05.2014. 12:30 ] @
Da ne otvaram novu temu, a zadatak isto iz elementarne matematike.
Za sve prirodne brojeve k, n i m 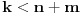 važi: važi: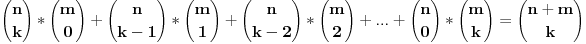 Kombinatorno je više nego jasno da važi jednakost. Traži se dokaz. Ništa ne uspevam. I još jedan koji ne znam da finiširam: Dokazati da se iz skupa od pet prirodnih brojeva uvek mogu izabrati 2 broja m i n tako da je  deljivo sa 15. deljivo sa 15.[ Sonec @ 23.05.2014. 12:59 ] @
[ miki069 @ 23.05.2014. 14:35 ] @
[ berazorica @ 25.05.2014. 08:23 ] @
Citat: Poslednja cifra četvrtog stepena prirodnog broja može biti 0, 1, 5 ili 6. Dakle, bar dva od odabranih pet brojeva imaju četvrti stepen koji završava istom cifrom, pa razlika ima poslednju cifru 0, tj. deljiva je sa 5. Za deljivost sa 3 dovoljno je rastaviti  na činioce. Od pet brojeva, bar dva daju isti ostatak pri deljenju sa 3, pa je njihova razlika deljiva sa 3, tj, činilac (m-n) je deljiv sa 3. na činioce. Od pet brojeva, bar dva daju isti ostatak pri deljenju sa 3, pa je njihova razlika deljiva sa 3, tj, činilac (m-n) je deljiv sa 3.[Ovu poruku je menjao berazorica dana 25.05.2014. u 09:33 GMT+1] [ miki069 @ 05.06.2014. 23:09 ] @
[ Nedeljko @ 06.06.2014. 07:34 ] @
[ Jbyn4e @ 06.06.2014. 18:05 ] @
@nedeljko:
Ako sam dobro shvatio, x=a/b, itd? A sa desne strane je b/a, ne a/b, tj 1/x? Onda ti početna nejednačina (ono na 4ti >= zbir) nije dobra jer je kod zbir u stvari 1/x+1/y...? Ostatak rešenja neću komentarisati jer nemam dovoljno znanja, samo mi je ovo zapalo za oko... jer je sa jedne strane a/b a sa druge b/a itd. P.S. Izvini, a ne znam ni kako se ovaj tex upotrebljava. [ Nedeljko @ 06.06.2014. 21:50 ] @
U pravu si. Dakle, meni treba nejednakost
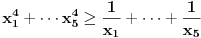 , ,odnosno 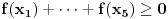 za za 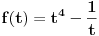 . .Ovako ne mogu direktno da iskoristim Jensenovu nejednakost jer mi treba 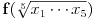 , a ne , a ne  jer znam da je jer znam da je 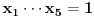 . No, to možemo postići uvođenjem smene . No, to možemo postići uvođenjem smene 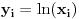 . Uslov . Uslov 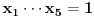 prelazi u uslov prelazi u uslov 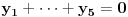 , a nejednakost dobija oblik , a nejednakost dobija oblik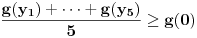 za za 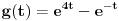 , ,pri čemu se lako proverava da  jeste konveksna funkcija. jeste konveksna funkcija.Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|