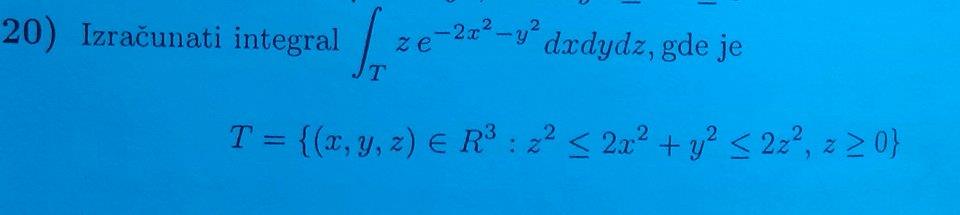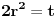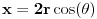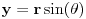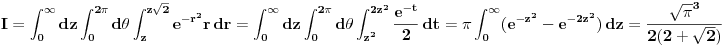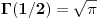Oba konusa su ti eliptički konusi, a ne kružni konusi.

Kada nađeš preseke postupaš isto kao u zadatku iz teme o izračunavanju zapremine.

A, kakve presjeke da nađem? Ako ovu dvostruku nejednakost posmatram kao jednačine,, rješenje je samo z = 0. A, to i jeste, sijeku se u 0, ali šta s tim...

U pravu si.
Jedini presek ime je zajedničko teme u koordinatnom početku.
U pitanju je nesvojstveni integral i ro do +beskonačno.
Problem je samo kako preći na ro i fi, pošto nema konačne elipse.

Ako uvrstim ove parametre, dobiću granicu za z, ali ne znam šta sa r i fi, da li tu r smije ići od 0 do 1, a fi od 0 do 2pi?

Milsim da je dobro je urađeno.
fi ode od nula do 2*pi.
ro ide od nula do +beskonačno.
Dobija se nesvojstveni integral po ro.

super, hvala puno,.. da li bi mi mogao samo objasniti zašto ro ide do +beskonačno...? to mi nije jasno..

Pokušala sam tako uraditi... Evo slike.. Ali, ne znam kako ovaj integral riješiti, zadnji, probala sam oarcijalnu inegraciju, ali i ne ide baš...?

Tesko ce to ici preko parcijalne. Uvedi smenu i onda prepoznaj Gama funkciju.

Ako uvedem tu smjenu, pojavice mi se koren iz t a i e na t.. opet ne vodi rjesenju... ako ste na to mislili... a, preko ove Gama funkcije ne znam kako ide... sta je to? Obicna smena ili..?

Ne može se rešiti kao neodređen integral.
Kao nesvojstveni, u datim granicama, može.
Gama funkciji ne smeta koren.

Jesi li iz neke Analize radila nesvojstvene integrale i u ookviru toga Gama funkciju?
Ako nisi, ne bi smela da dobiješ ovakav zadatak.
Ako jesi, a zaboravila si, evo literature:
https://imi.pmf.kg.ac.rs/compo...-integral-marta-milosevic.html

, .

.

Naravno, .