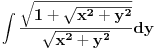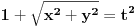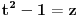Kreni od smene

ali trebace i posle ove jos barem 2 smene

Hvala na trudu :)

posle toga dobije ovo....




probam da ga uradim parcijalnom integracijom, ali se zakomplikuje... :)

uzmem da je u=t, a integral v uradim smjenom

Resenje se ne moze izraziti preko elementarnih funkcija, odnosno, resenje ukljucuje takozvane specijalne funkcije. U ovom slucaju ce se svoditi na elipticki integral integral prve i druge vrste (source: wolfram).

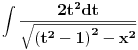Mislim da si lose odradio izvod ... cinimi se da treba da bude -2t^2(t^2-1) kroz ovo sto si napisao ... proveri
zatim sam isao na smenu t^2-1=z^2
pa z^2 - x^2 = p^2
i mislim da sam na kraju dobio ovako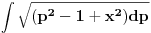

Wolfram vraca resenje van domena elementarnih funkcija, ali potrudi se da resis :)

Joj, ne vjerujem da sam pogrijesio, pogledaj jos jednom, jer imas i u nazivniku t na 2 -1.... :/ sad ne znam... Sonec imas li ti mozda neko konkretno RJ. ? :) Hvala...

Jel ovo kompletan zadatak ili je deo nekog drugog zadatka?
Ako je deo, onda napiši kompletan zadatak.

=









=

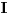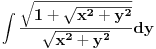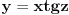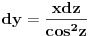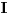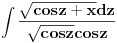Smjena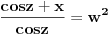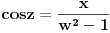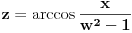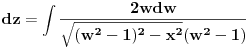












Uvrstavajuci posljednje izraze u integral I dobijamo sledeci integral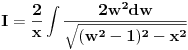




Parcijalnom integracijom uvodeci da je


i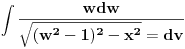


v se racuna preko smjene 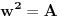i dobiva se tablicni integral
nakon toga se dobiva jos jedan inetgral sa podintegralnom funkcijom lntg[f(w)]








_{[Ovu poruku je menjao different dana 10.03.2015. u 15:28 GMT+1]}