[ Diskriminanta @ 02.01.2015. 06:50 ] @
 Na slici su u uglu AOB konstruisani ravnokraki trouglovi OCD i ODE tako da su tačke CDE na istoj pravoj. Može li se to učiniti u bilo kom uglu i kako? |
|
[ Diskriminanta @ 02.01.2015. 06:50 ] @
[ zzzz @ 02.01.2015. 17:46 ] @
To je problem trisekcije ugla.Dakle ako znaš trećinu ugla konstrukcija je jednostavna kao na slici. 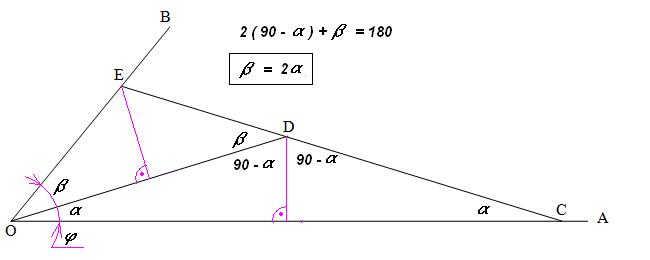 [ Diskriminanta @ 03.01.2015. 21:32 ] @
Bravo Milane!
A za nagradu šaljem ti moj uređaj iliti pribor za trisekciju ugla. On je vrlo jednostavan i kad je van upotrebe izgleda kao olovka. Ovde se u stvari vidi koliko je i Arhimedovo rešenje mehaničko - samo što je on umesto drvenih i metalnih delova upotrebio svoje ruke kao mehanička pomagala. Ne znam da li postoji i takva geometrija koja koristi i druge trajektorije materijalnih tela, a ne samo lenjira i šestara.  Uređaj se upotrebljava tako da vrh gornje polovine "olovke" kliza po donjoj polovini. I da ne objašnjavam - sve se jasno vidi sa slike. Upotrebio sam što manje oznaka. [ Nedeljko @ 03.01.2015. 22:09 ] @
Naravno da se izučavaju i drugi skupovi instrumenata. Arhimedovo rešenje je pomoću šestara i lenjira sa dva zareza.
[ Diskriminanta @ 04.01.2015. 06:17 ] @
Lenjir sa dva zareza je isto šestar ali se njegov centar rotacije kreće još i po pravoj liniji.
Trebalo bi malo detaljnije objasniti uslove upotrebe lenjira i šestara jer, na primer, može se konstruisati trećina ugla sa lenjirom i šestarom kao na slici dole, tako da se tim mestom na lenjiru, na kojem je zarez, pomera slobodni kraj šestara dok lenjir ne dođe u crtkani položaj.  [ Nedeljko @ 04.01.2015. 17:33 ] @
Upotreba lenjira znači samo konstrukciju prave kroz date dve tačke, a šestara samo konstrukciju kruga oko datog centra kroz datu tačku. Pritom možemo onstruisati i presečne tačke konstruisanih objekata.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|