Izvod po je

.

Obzirom da je svaki od sabiraka unutar zagrada ograničen jedinicom, parcijalni izvod po je po apsolutnoj vrednosti ograničen sa , pa je neprekidan u tački , tako da je tvoje rešenje tačno.

Hvala Nedeljko.

E, da, moje rešenje je nepotpuno. Neophodno je obrazložiti i neprekidnost u tački što sledi iz

.

Izvinjavam se, ali evo je i trećeg izdanja zbirke (skripte) i autori opet tvrde da nije diferencijabilna.

Urade mešovite parcijalne izvode drugog reda u tački (0,0).
Dobija se, bez greške, da je:

Fxy(0,0) = -1

Fyx(0,0) = +1.

Pošto su mešoviti izvodi različiti, zaključuju da funkcija nije diferencijabilna u tački (0,0).

Teorema o jednakosti mešovitih drugih izvoda ima zahtev neprekidnosti prvih izvoda.
Ali ne i uslov diferencijabilnosti.

Pošto je Nedeljko obrazložio neprekidnost izvoda po x, mora da pada neprekidnost izvoda po y.
Ili pada teorema o jednakosti mešovitih izvoda.
Ili pada interpretacija teoreme o jednakosti mešovitih izvoda od strane autora zbirke.

Po definiciji se dobija da je funkcija diferencijabilna.


Ajde da pogledamo izvod po .



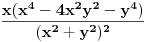
Ako bi i ovo bila neprekidna funkcija u (0,0) ne bi smeli mešoviti izvodi da budu različiti?
Ili bi smeli?




_{[Ovu poruku je menjao miki069 dana 03.01.2017. u 19:35 GMT+1]}

Neprekidan je i izvod po y.

Teorema o jednakosti mešovitih izvoda drugog reda ne zahteva neprekidnost parcijalnih izvoda prvog reda.
Samo njihovo postojanje.