Nije otvoren, već zatvoren.

Ok, znam samo da je podskup zatvorenog skupa. Zasto je zatvoren?

Uh, upravo sam shvatila da ne moraju da budu ni singularne, ako su parne dimenzije, ne stoji ni argument za determinantu.

Pa, hajde, posmatraj niz ososimetričnik matrica koji konvergira nekoj matrici. Da li je i ona kososimetrična i zašto?

Posmatram matricu kao -torku, konvergenciju posmatram po svakom clanu uredjene -torke. Ako neki niz tezi nekom a, onda niz tezi -a. Po glavnoj dijagonali su svakako nule, znaci da i granicna matrica mora da bude kososimetricna. Interesantno.

Originalan zadatak je bio ovakav:
Kejlijevo preslikavanje je zadato sa
na skupu realnih kvadratnih matrica A takvih da je I+A invertibilno.
1) Dokazati da je C involucija, difeomorfizam, da ortogonalne matrice slika u kososimetricne i obrnuto.
2) Posmatramo matricnu grupu G koja je podgrupa od invertibilnih matrica. Posmatramo podskup od G svih matrica A za koje je Kejlijevo preslikavanje definisano (nazovimo ga recimo P). Ako je slika C(P) otvoren skup u prostoru realnih kvadratnih matrica, onda je G Lijeva grupa.
3) Na osnovu prethodnog zakljucujemo da su ortogonalne matrice Lijeva grupa.


Posto se Kejlijevim preslikavanjem orotgonalne matrice slikaju u kososimetricne, mislila sam da za 3 treba dokazati da je skup koso simetricnih otvoren u . U stvari, mi Kejlijevim preslikavanjem slikamo podskup orotogonalnih matrica (one ortogonalne kod kojih je I+A invertibilno) u neki podskup kososimetricnih. Da bi se iskoristilo 2, u stvari treba dokazati da je taj podskup otvoren u . Hvala puno, ovo mi daje nove teme za razmisljanje.

<sub>[Ovu poruku je menjao sabandijillaa dana 18.04.2015. u 15:21 GMT+1]

[Ovu poruku je menjao sabandijillaa dana 18.04.2015. u 17:56 GMT+1]</sub>

Inace, 1 sam uspela da uradim, mogu da ispisem resenje ako nekog zanima. Cini mi se da je 2 glavni deo zadatka.

Podgrupa Lijeve grupe, koja je pritom otvoren podskup te Lijeve grupe je sama Lijeva grupa.

Grupa je otvorena akko ima nepraznu unutrašnjost.

Neka je C(P)=U otovren skup. P je inverzna slika od U pri preslikavanju C jer je C bijekcija kao involucija. Obzirom da je C neprekidno, P je otvoren skup.

Obzirom da je P neprazan otvoren podskup od G, G je Lijeva grupa.

Hvala Nedeljko, trebalo mi je malo vremena da vidim zasto vaze tvredjenja koja si naveo.
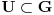
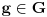
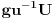
Ako grupa ima nepraznu unutrasnjost, onda postoji neki otvoreni skup . Transliramo U po grupi G i dobijemo da je otvorena, tj. za proizvoljan elemenat i za bilo koje u iz U ckup je otvorena okolina od g cela sadrzana u grupi G. Znaci da je G otvorena.

H je podgrupa od G (algebarski) ako je podskup i ima strukturu grupe u odnosu na operacije iz G.
H je topoloska podgrupa od G ako je prethodno + topoloski potprostor (u odnosu na indukovanu topologiju).
H je Lijeva podgrupa od G ako je prethodno + podmnogostrukost.

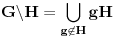
Ako je H otvorena podgrupa topoloske grupe G, onda je H i zatvorena, jer je komplement otvoren kao unija otvorenih skupova.

Znaci da podgrupa topoloske grupe moze da bude ili otvorena i zatvorena (clopen) ili da ima praznu unutrasnjost.
Zatvorena podgrupa Lijeve grupe je Lijeva grupa (closed subgroup theorem). Zato se zadatak svodi to da se dokaze da G ima nepraznu unutrasnjost.

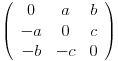
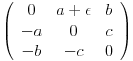
Ispada da za 3. deo zadatka, da bismo primenili prethodno, traba da dokazemo da skup koso-simetricnih matrica ima nepraznu unutrasnjost. Medjutim, za bilo koju koso-simetricnu matricu, npr. u 3 dimenzije , u svakoj njenoj okolini postoji matrica koja nije koso-simetricna, npr. . Ispada da skup koso-simetricnih matrica nema unutrasnjost, pa ne moze da se primeni 2. Da li opet negde gresim u razmisljanju?

_{[Ovu poruku je menjao sabandijillaa dana 25.04.2015. u 17:47 GMT+1]}