[ Barbarian22 @ 15.06.2015. 20:16 ] @
|
| Koristeci rjesenja jednacine z^5 - 1 = 0 odrediti cos( (2*Pi) / 5 ) i sin ( (2*Pi) / 5) .
Odredim rjesenja ove jednacine, moduo mi bude 1,argument 0 i nadjem onih 5 rjesenja. Sad mi nije jasno kako da odredim ovo kosinus i sinus na osnovu tih rjesenja. Pomoc :D |
[ mjanjic @ 16.06.2015. 00:06 ] @
Tih 5 rešenja su x = e^(i(2kPi/5)), k=0,1,2,3,4
Dakle, prvo rešenje je x = e^0 = 1 (očigledno i iz jednačine).
Traženo rešenje je ovo drugo, tj. e^(i(2Pi/5)) = cos(2Pi/5)+i*sin(2Pi/5).
Sada, z^5 - 1 = 0 = (z - 1) * (1 + z + z^2 + z^3 + z^4).
Prvo rešenje je z=1, a ostala 4 rešenja su različita od 1 i dobijaju se iz jednačine: 1 + z + z^2 + z^3 + z^4 = 0.
Sada podeliš ovu jednčinu sa z^2 (pošto z nije nula kada važi ova jednakost), pa je
z^(-2) + z^(-1) + 1 + z + z^2 = 0.
Sada se iskoristi smena y = z + 1/z, pa se dobija jednačina: y^2 + y - 1 = 0.
Od dva rešenja ove kvadratne jednačine za smenu je validno samo jedno, tj. (-1 + sqrt(5))/2, jer je drugo negativno, a za argument 2Pi/5 (drugo rešenje polazne jednačine) važi z + 1/z = z + z_k = 2*cos(2Pi/5) što je pozitivno, gde je z_k konjugovano-kompleksan broj od z, pa je:
z + 1/z = 2*cos(2Pi/5) = (-1 + sqrt(5))/2,
tj.
cos(2pi/5) = (-1 + sqrt(5))/4
sin se nalazi iz jednakosti sin^2 + cos^2 = 1.
[ Barbarian22 @ 16.06.2015. 09:14 ] @
Kako si nakon smjene y = z + 1/z dobio da je y^2 + y - 1 = 0. Kako si dobio ovaj minus ispred jedinice,zar nije trebalo y^2 + y + 1 =0 ?
[ bobanex @ 16.06.2015. 11:09 ] @
Evo ovako:
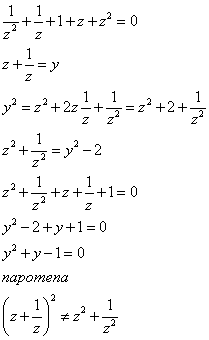
[ bobanex @ 16.06.2015. 11:15 ] @
[ Barbarian22 @ 16.06.2015. 11:37 ] @
E hvala, sad mi je mnogo jasnije. Rupe iz srednje skole :S
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.