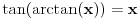
za svako .

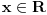
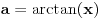
Neka je i .

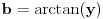
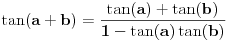
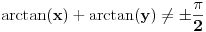
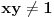
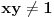
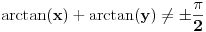
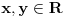
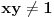
kad god je sve definisano, odnosno kada je i . Obzirom da iz sledi , možemo zaključiti da za ma koje za koje je važi

.

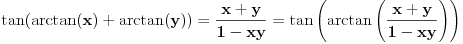
Odavde sledi da je



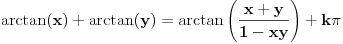
jer se brojevi sa istim tangensom razlikuju za celobrojan umnožak broja .

Posmatraj funkciju

.

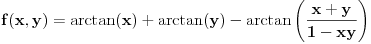
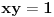
Ona je definisana u celoj ravni van hiperbole i neprekidna je, a vrednosti su joj u diskretnom skupu celobrojnih umnožaka broja . Pošto je neprekidna, a vrednosti su joj u diskretnom skupu, ona mora biti konstantna na svakoj komponenti povezanosti domena. Ima ih tri:

,
,
.

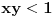
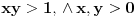
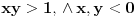
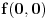
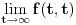
Na prvoj vrednost funkcije možemo odrediti računajući , na drugoj računajući i na trećoj računajući .

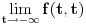
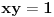
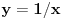
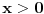
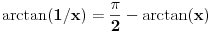
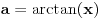
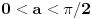
Ostao je slučaj kada je , odnosno . Ako je , onda je . Jer je za ispunjeno i

,

,

.

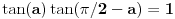
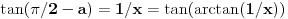
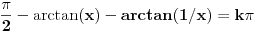
Odavde sledi da neprekidna funkcija



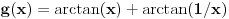
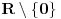
definisana na ima vrednosti u diskretnom skupu. I ona je stoga konstantna na svakoj od dve komponente povezanosti na kojima joj vrednost možemo odrediti računanjem na primer i .

Nedeljko, hvala puno, sada mi je potpuno jasno! :)

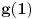
Ako si nekako naslutio , onda posmatraš navedenu funkciju . Ona je konstantna na komponentama povezanosti domena na kojima su joj parcijalni izvodi jednaki nuli.
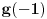